正确率60.0%在等腰直角三角形$${{A}{B}{C}}$$中,$$A B=A C=2$$,点$${{P}}$$是边$${{A}{B}}$$上异于$${{A}{、}{B}}$$的一点,光线从点$${{P}}$$出发,经$$B C, \ C A$$反射后又回到点$${{P}{(}}$$如图所示$${{)}}$$,若光线$${{Q}{R}}$$经过$${{△}{A}{B}{C}}$$的重心,则$${{A}{P}{=}}$$()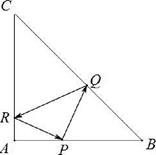
C
A.$${{1}}$$
B.$$\frac{1} {2}$$
C.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
D.$$\frac{4} {3}$$
2、['直线的一般式方程及应用']正确率80.0%点$$M ( x_{0}, \ y_{0} )$$是直线$$A x+B y+C=0$$上的点,则直线方程可表示为()
A
A.$$A ( x-x_{0} )+B ( y-y_{0} )=0$$
B.$$A ( x-x_{0} )-B ( y-y_{0} )=0$$
C.$$B ( x-x_{0} )+A ( y-y_{0} )=0$$
D.$$B ( x-x_{0} )-A ( y-y_{0} )=0$$
3、['两条直线垂直', '直线的一般式方程及应用']正确率60.0%与直线$$2 x-y-1=0$$垂直,且在$${{y}}$$轴上的截距为$${{4}}$$的直线的一般式方程是()
A
A.$$x+2 y-8=0$$
B.$$x+2 y-8=0$$或$$x+2 y+8=0$$
C.$$x-2 y+8=0$$
D.$$x-2 y+8=0$$或$$x-2 y-8=0$$
4、['直线的一般式方程及应用']正确率60.0%在同一平面直角坐标系中,直线$${{l}_{1}}$$:$$a x-y+b=0, ~ l_{2}$$:$$b x+y-a=0 ( a b \neq0 )$$的位置可能是()
D
A.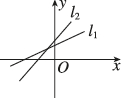
B.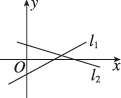
C.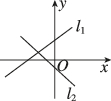
D.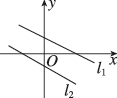
正确率60.0%若$$( 1+i )^{2}+| 2 i |=\overline{{z}}$$,其中$$z=a+b i \alpha, \, \, b \in R,$$为虚数单位),则直线$$b x-a y+a=0$$的斜率为()
A
A.$${{−}{1}}$$
B.$${{1}}$$
C.$${\sqrt {3}}$$
D.$$\frac{\sqrt{3}} {3}$$
6、['直线的一般式方程及应用']正确率19.999999999999996%直线$${{l}}$$经过直线$$2 x-3 y-2=0$$与直线$$x+3 y-1=0$$的交点,且它的斜率等于直线$$x-2 y=0$$的斜率的$${{2}}$$倍,则直线$${{l}}$$的方程为()
C
A.$$x+y-1=0$$
B.$$2 x+y-2=0$$
C.$$x-y-1=0$$
D.$$2 x-y-2=0$$
7、['直线的一般式方程及应用', '两条直线平行']正确率40.0%过点$$P ~ ( 1, ~ 2 )$$且与直线$$3 x+y-1=0$$平行的直线方程是()
A
A.$$3 x+y-5=0$$
B.$$x+3 y-7=0$$
C.$$x-3 y+5=0$$
D.$$x \!-\! 3 y \!-\! 5 \!=\! 0$$
8、['直线的点斜式方程', '直线的一般式方程及应用', '两条直线平行', '直线的斜率']正确率60.0%经过$$P ( 2, 1 )$$的直线$${{l}}$$到$$A ( 1, 1 ), ~ B ( 3, 5 )$$两点的距离相等,则直线$${{l}}$$的方程为()
C
A.$$2 x-y-3=0$$
B.$$x+2 y-4=0$$
C.$$2 x-y-3=0$$或$${{x}{=}{2}}$$
D.$$x+2 y-4=0$$或$${{x}{=}{2}}$$
9、['直线的点斜式方程', '两条直线垂直', '直线的一般式方程及应用']正确率60.0%过点$$A ( 3, 3 )$$且垂直于直线$$4 x+2 y-7=0$$的直线方程为()
D
A.$$y=\frac{1} {2} x+2$$
B.$$y=-2 x+7$$
C.$$y=\frac{1} {2} x+\frac{5} {2}$$
D.$$y=\frac{1} {2} x+\frac{3} {2}$$
10、['直线中的对称问题', '直线的一般式方程及应用']正确率60.0%直线$$y=2 x-2$$与直线$${{l}}$$关于$${{y}}$$轴对称,则直线$${{l}}$$的方程为()
B
A.$$y=-2 x+2$$
B.$$y=-2 x-2$$
C.$$y=2 x+2$$
D.$$y=\frac1 2 x-1$$
1. 解析:
在等腰直角三角形 $$ABC$$ 中,$$AB = AC = 2$$,建立坐标系,设点 $$A(0,0)$$,$$B(2,0)$$,$$C(0,2)$$。点 $$P$$ 在 $$AB$$ 上,设 $$P(p,0)$$,其中 $$0 < p < 2$$。
光线从 $$P$$ 出发,经 $$BC$$ 反射到 $$Q$$,再经 $$CA$$ 反射到 $$R$$,最后回到 $$P$$。利用反射定律,可以构造 $$P$$ 关于 $$BC$$ 的对称点 $$P'$$ 和关于 $$CA$$ 的对称点 $$P''$$,则光线路径对应于直线 $$P'Q$$ 和 $$P''R$$。
计算对称点:
- $$P$$ 关于 $$BC$$ 的对称点 $$P'$$ 为 $$(2, 2-p)$$。
- $$P$$ 关于 $$CA$$ 的对称点 $$P''$$ 为 $$(-p, 0)$$。
光线 $$QR$$ 经过重心 $$G$$,重心坐标为 $$(\frac{2+0+0}{3}, \frac{0+2+0}{3}) = (\frac{2}{3}, \frac{2}{3})$$。
由 $$P'$$、$$G$$、$$P''$$ 三点共线,斜率相等:
$$\frac{\frac{2}{3} - (2 - p)}{\frac{2}{3} - 2} = \frac{\frac{2}{3} - 0}{\frac{2}{3} - (-p)}$$
解得 $$p = \frac{4}{3}$$,故选 D。
2. 解析:
点 $$M(x_0, y_0)$$ 在直线 $$Ax + By + C = 0$$ 上,满足 $$Ax_0 + By_0 + C = 0$$。
直线方程可以表示为 $$A(x - x_0) + B(y - y_0) = 0$$,展开后与原方程一致。故选 A。
3. 解析:
与直线 $$2x - y - 1 = 0$$ 垂直的直线斜率为 $$-\frac{1}{2}$$。
在 $$y$$ 轴上截距为 4,直线方程为 $$y = -\frac{1}{2}x + 4$$,化为一般式为 $$x + 2y - 8 = 0$$。故选 A。
4. 解析:
直线 $$l_1: ax - y + b = 0$$ 斜率为 $$a$$,$$y$$ 截距为 $$b$$。
直线 $$l_2: bx + y - a = 0$$ 斜率为 $$-b$$,$$y$$ 截距为 $$a$$。
选项 B 中,$$l_1$$ 斜率为正,$$y$$ 截距为正;$$l_2$$ 斜率为负,$$y$$ 截距为正,符合 $$a > 0$$,$$b < 0$$ 的情况。故选 B。
5. 解析:
计算 $$(1 + i)^2 + |2i| = 1 + 2i + i^2 + 2 = 2 + 2i$$。
设 $$\overline{z} = 2 + 2i$$,则 $$z = 2 - 2i$$,即 $$a = 2$$,$$b = -2$$。
直线方程为 $$-2x - 2y + 2 = 0$$,斜率为 $$-1$$。故选 A。
6. 解析:
解方程组 $$2x - 3y - 2 = 0$$ 和 $$x + 3y - 1 = 0$$,得交点 $$(1, 0)$$。
直线 $$x - 2y = 0$$ 的斜率为 $$\frac{1}{2}$$,所求直线斜率为 $$2 \times \frac{1}{2} = 1$$。
直线方程为 $$y = x - 1$$,即 $$x - y - 1 = 0$$。故选 C。
7. 解析:
与直线 $$3x + y - 1 = 0$$ 平行的直线斜率为 $$-3$$。
过点 $$P(1, 2)$$ 的直线方程为 $$y - 2 = -3(x - 1)$$,即 $$3x + y - 5 = 0$$。故选 A。
8. 解析:
直线 $$l$$ 过 $$P(2, 1)$$,且到 $$A(1, 1)$$ 和 $$B(3, 5)$$ 距离相等。
若 $$l$$ 与 $$AB$$ 平行,斜率为 $$\frac{5 - 1}{3 - 1} = 2$$,方程为 $$y - 1 = 2(x - 2)$$,即 $$2x - y - 3 = 0$$。
若 $$l$$ 过 $$AB$$ 中点 $$(2, 3)$$,斜率为 $$\frac{3 - 1}{2 - 2}$$ 不存在,即 $$x = 2$$。
综上,直线方程为 $$2x - y - 3 = 0$$ 或 $$x = 2$$。故选 C。
9. 解析:
直线 $$4x + 2y - 7 = 0$$ 的斜率为 $$-2$$,与之垂直的直线斜率为 $$\frac{1}{2}$$。
过点 $$A(3, 3)$$ 的直线方程为 $$y - 3 = \frac{1}{2}(x - 3)$$,即 $$y = \frac{1}{2}x + \frac{3}{2}$$。故选 D。
10. 解析:
直线 $$y = 2x - 2$$ 关于 $$y$$ 轴对称,将 $$x$$ 替换为 $$-x$$,得到 $$y = 2(-x) - 2$$,即 $$y = -2x - 2$$。故选 B。
.jpg)