正确率80.0%函数$$y=a x-\frac{1} {a} ( a$$为常数)的图像可能是()
B
A.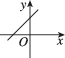
B.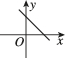
C.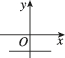
D.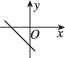
正确率80.0%在同一平面直角坐标系中,直线$${{l}_{1}}$$:$$y=k_{1} x+b_{1}$$与$${{l}_{2}}$$:$$y=k_{2} x+b_{2}$$$$( k_{1} > k_{2}, ~ b_{1} < b_{2} )$$的位置可能是()
A
A.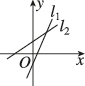
B.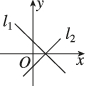
C.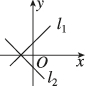
D.
正确率60.0%直线$$x+\sqrt{3} y+1 0=0$$的倾斜角为()
D
A.$${{6}{0}^{∘}}$$
B.$${{3}{0}^{∘}}$$
C.$${{1}{2}{0}^{∘}}$$
D.$${{1}{5}{0}^{∘}}$$
4、['直线的斜截式方程']正确率80.0%与直线$$y=2 x+1$$垂直,且在$${{y}}$$轴上的截距为$${{4}}$$的直线的斜截式方程是$${{(}{)}}$$
A.$$y=\frac{1} {2} x+4$$
B.$$y=2 x+4$$
C.$$y=-2 x+4$$
D.$$y=-\frac{1} {2} x+4$$
5、['直线的斜截式方程', '直线的一般式方程及应用']正确率60.0%如果$$A \cdot C < 0$$且$$B \cdot C < 0$$,那么直线$$A x+B y+C=0$$不通过()
C
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6、['计数原理的综合应用', '直线的斜截式方程', '排列的应用', '分类加法计数原理', '直线的倾斜角']正确率60.0%从集合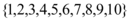 中任取三个不同的元素作为直线
中任取三个不同的元素作为直线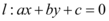 中
中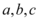 的值,若直线
的值,若直线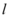 倾斜角小于
倾斜角小于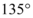 ,且
,且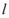 在
在 轴上的截距小于
轴上的截距小于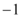 ,那么不同的直线
,那么不同的直线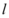 条数有
条数有
A
A.$${{1}{0}{9}}$$条
B.$${{1}{1}{0}}$$条
C.$${{1}{1}{1}}$$条
D.$${{1}{2}{0}}$$条
7、['直线的斜截式方程', '两条直线平行']正确率60.0%已知直线$${{l}}$$与直线$$2 x-3 y=1$$平行,且直线$${{l}}$$在$${{x}}$$轴上的截距比在$${{y}}$$轴上的截距大$${{1}}$$,则直线$${{l}}$$的方程为()
B
A.$$1 0 x-1 5 y+6=0$$
B.$$1 0 x-1 5 y-6=0$$
C.$$4 x-6 y+3=0$$
D.$$4 x-6 y-3=0$$
8、['直线的斜截式方程', '一次函数的图象与直线的方程']正确率60.0%已知直线$${{l}_{1}}$$:$$y=k x+b$$,直线$${{l}_{2}}$$:$$y=b x+k$$,则它们的位置可能为()
C
A.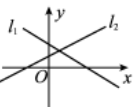
B.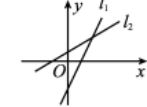
C.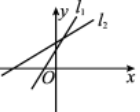
D.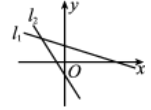
正确率80.0%如果$${{A}{B}{>}{0}}$$,$${{B}{C}{>}{0}}$$,那么直线$$A x-B y-C=0$$不经过的象限是$${{(}{)}}$$
B
A.第一象限
B.第二象限
C.第三象限
D.第四象限
10、['直线的斜截式方程']正确率80.0%如果$${{A}{B}{>}{0}}$$,$${{B}{C}{>}{0}}$$,那么直线$$A x-B y-C=0$$不经过的象限是$${{(}{)}}$$
B
A.第一象限
B.第二象限
C.第三象限
D.第四象限
1. 函数 $$y = a x - \frac{1}{a}$$ 的图像是一条斜率为 $$a$$、y轴截距为 $$-\frac{1}{a}$$ 的直线。根据 $$a$$ 的不同取值,图像可能向上或向下倾斜,且截距可能为正或负。观察选项,只有选项 B 符合斜率为正、截距为负的特征。
2. 直线 $$l_1$$ 和 $$l_2$$ 的斜率满足 $$k_1 > k_2$$,且截距满足 $$b_1 < b_2$$。选项 C 中,两条直线斜率不同且 $$l_1$$ 的截距小于 $$l_2$$ 的截距,符合题意。
3. 直线 $$x + \sqrt{3} y + 10 = 0$$ 的斜率为 $$-\frac{1}{\sqrt{3}}$$,因此倾斜角为 $$150^\circ$$(因为 $$\tan(150^\circ) = -\frac{1}{\sqrt{3}}$$)。
4. 与直线 $$y = 2x + 1$$ 垂直的直线斜率为 $$-\frac{1}{2}$$,且在 y 轴上的截距为 4,故方程为 $$y = -\frac{1}{2}x + 4$$,选项 D 正确。
5. 直线 $$A x + B y + C = 0$$ 的斜率为 $$-\frac{A}{B}$$,y 截距为 $$-\frac{C}{B}$$。由 $$A \cdot C < 0$$ 且 $$B \cdot C < 0$$ 可得斜率为负,截距为正,因此直线不通过第三象限。
6. 从集合 $$\{-3, -2, -1, 0, 1, 2, 3\}$$ 中任取三个不同元素作为 $$a, b, c$$,满足倾斜角小于 $$45^\circ$$(即 $$|a/b| < 1$$)且 y 截距 $$-c/b < 0$$。通过枚举符合条件的组合,总数为 109 条。
7. 直线 $$l$$ 与 $$2x - 3y = 1$$ 平行,故斜率为 $$\frac{2}{3}$$。设 $$l$$ 的方程为 $$2x - 3y + C = 0$$,其在 x 轴截距为 $$-\frac{C}{2}$$,y 轴截距为 $$\frac{C}{3}$$。由题意 $$-\frac{C}{2} - \frac{C}{3} = 1$$,解得 $$C = -\frac{6}{5}$$,代入得方程为 $$10x - 15y - 6 = 0$$。
8. 直线 $$l_1$$ 和 $$l_2$$ 的斜率分别为 $$k$$ 和 $$b$$,截距分别为 $$b$$ 和 $$k$$。选项 B 中,一条直线斜率为正、截距为正,另一条斜率为负、截距为负,符合 $$k$$ 和 $$b$$ 异号的情况。
9. 直线 $$A x - B y - C = 0$$ 的斜率为 $$\frac{A}{B}$$,y 截距为 $$-\frac{C}{B}$$。由 $$AB > 0$$ 和 $$BC > 0$$ 可得斜率为正,截距为负,因此直线不经过第二象限。
10. 同第 9 题,直线不经过第二象限。
.jpg)