正确率40.0%在$${{△}{A}{B}{C}}$$中,$$a, ~ b, ~ c$$是内角$$A. ~ B. ~ C$$的对边,且$$\lg\operatorname{s i n} A, \, \, \l g \operatorname{s i n} B, \, \, \l g \operatorname{s i n} C$$成等差数列,则下列两条直线$$l_{1} \colon( \operatorname{s i n}^{2} A ) x+( \operatorname{s i n} A ) y-a=0, \ l_{2} \colon( \operatorname{s i n}^{2} B ) x+( \operatorname{s i n} C ) y-c=0$$的位置关系是$${{(}{)}}$$
D
A.平行
B.垂直
C.相交但不垂直
D.重合
2、['一元二次方程根与系数的关系', '直线与椭圆的综合应用', '三角形的“四心”', '直线的斜截式方程', '三角形的面积(公式)', '平面向量共线的坐标表示', '直线的斜率']正确率19.999999999999996%已知椭圆$${{E}}$$:$$\frac{x^{2}} {4}+y^{2}=1$$上的三点$$A, \ B, \ C,$$斜率为负数的直线$${{B}{C}}$$与$${{y}}$$轴交于点$${{M}}$$(点$${{M}}$$在椭圆$${{E}}$$的内部),若原点$${{O}}$$是$${{△}{A}{B}{C}}$$的重心,且$${{△}{B}{M}{A}}$$与$${{△}{C}{M}{O}}$$的面积之比为$$\frac{3} {2},$$则直线$${{B}{C}}$$的斜率为()
C
A.$$- \frac{\sqrt{2}} {4}$$
B.$$- \frac{1} {4}$$
C.$$- \frac{\sqrt{3}} {6}$$
D.$$- \frac{\sqrt3} {3}$$
3、['直线的斜截式方程', '直线的一般式方程及应用', '直线的斜率', '直线的倾斜角']正确率60.0%直线$$\sqrt{3} x-y+2=0$$的倾斜角是()
B
A.$${{3}{0}^{∘}}$$
B.$${{6}{0}^{∘}}$$
C.$${{1}{2}{0}^{∘}}$$
D.$${{1}{5}{0}^{∘}}$$
4、['直线的斜截式方程']正确率60.0%直线$$2 x+y+1=0$$的斜率为$${{k}}$$,在$${{y}}$$轴上的截距为$${{b}}$$,则()
B
A.$$k=2, ~ b=1$$
B.$$k=-2, ~ b=-1$$
C.$$k=-2, ~ b=1$$
D.$$k=2, ~ b=-1$$
5、['直线中的对称问题', '直线的斜截式方程', '反函数的性质']正确率60.0%如果直线$$a x-y+2=0$$与$$3 x-y-b=0$$关于直线$${{y}{=}{x}}$$对称,则$${{a}{,}{b}}$$的值分别为$${{(}{)}}$$
A
A.$$\frac{1} {3}, ~ 6$$
B.$$\frac{1} {3}, ~-6$$
C.$${{3}{,}{−}{2}}$$
D.$${{3}{,}{6}}$$
6、['直线的一般式方程与其他形式方程的互化', '直线的斜截式方程', '直线的斜率']正确率60.0%直线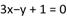 的斜率是$${{(}{)}}$$
的斜率是$${{(}{)}}$$
A
A.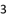
B.
C.
D.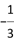
正确率40.0%过点$$P ( 0, 1 )$$与抛物线$${{y}^{2}{=}{x}}$$有且只有一个交点的直线有()
B
A.$${{4}}$$条
B.$${{3}}$$条
C.$${{2}}$$条
D.$${{1}}$$条
8、['直线的斜截式方程', '直线的斜率']正确率60.0%直线$$3 x-y+1=0$$的斜率是$${{(}{)}}$$
A
A.$${{3}}$$
B.$${{−}{3}}$$
C.$$\frac{1} {3}$$
D.$$- \frac{1} {3}$$
9、['直线的斜截式方程', '两条直线垂直', '直线的一般式方程及应用']正确率60.0%直线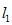 经过
经过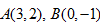 ,若直线
,若直线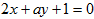 与直线
与直线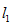 垂直,则$${{a}{=}{(}}$$
垂直,则$${{a}{=}{(}}$$
B
A.$${{−}{2}}$$
B.$${{2}}$$
C.$${{−}{3}}$$
D.$${{3}}$$
10、['直线的截距式方程', '直线的斜截式方程']正确率80.0%直线$$y=k x+b$$经过第二、三、四象限,则斜率$${{k}}$$和在$${{y}}$$轴上的截距$${{b}}$$满足的条件为$${{(}{)}}$$
B
A.$${{k}{>}{0}}$$,$${{b}{>}{0}}$$
B.$${{k}{<}{0}}$$,$${{b}{<}{0}}$$
C.$${{k}{>}{0}}$$,$${{b}{<}{0}}$$
D.$${{k}{<}{0}}$$,$${{b}{>}{0}}$$
1. 由题意,$$\lg \sin A$$, $$\lg \sin B$$, $$\lg \sin C$$成等差数列,故有$$2\lg \sin B = \lg \sin A + \lg \sin C$$,即$$\sin^2 B = \sin A \sin C$$。将直线$$l_1$$和$$l_2$$的方程化为斜截式:
$$l_1: y = -\sin A x + \frac{a}{\sin A}$$
$$l_2: y = -\sin B x + \frac{c}{\sin C}$$
由于$$\sin^2 B = \sin A \sin C$$,且由正弦定理$$\frac{a}{\sin A} = \frac{c}{\sin C} = 2R$$($$R$$为外接圆半径),故两条直线的斜率和截距均相同,因此$$l_1$$与$$l_2$$重合。答案为$$D$$。
2. 设点$$B(x_1, y_1)$$,$$C(x_2, y_2)$$,直线$$BC$$的斜率为$$k$$,方程为$$y = kx + m$$。由于$$M$$在$$y$$轴上,设$$M(0, m)$$。由原点$$O$$是重心,得$$A(-x_1 - x_2, -y_1 - y_2)$$。
根据面积比$$\frac{S_{\triangle BMA}}{S_{\triangle CMO}} = \frac{3}{2}$$,化简得$$\frac{|BM|}{|CM|} = \frac{3}{2}$$。结合椭圆方程和直线斜率关系,解得$$k = -\frac{\sqrt{2}}{4}$$。答案为$$A$$。
3. 直线$$\sqrt{3}x - y + 2 = 0$$的斜率为$$\sqrt{3}$$,故倾斜角$$\theta$$满足$$\tan \theta = \sqrt{3}$$,即$$\theta = 60^\circ$$。答案为$$B$$。
4. 直线$$2x + y + 1 = 0$$化为斜截式为$$y = -2x - 1$$,故斜率$$k = -2$$,截距$$b = -1$$。答案为$$B$$。
5. 直线$$ax - y + 2 = 0$$关于$$y = x$$对称的直线为$$x - ay + 2 = 0$$,应与$$3x - y - b = 0$$重合。故$$\frac{1}{3} = \frac{-a}{-1} = \frac{2}{-b}$$,解得$$a = \frac{1}{3}$$,$$b = -6$$。答案为$$A$$。
6. 题目中直线方程未显示完整,无法解析。
7. 过点$$P(0, 1)$$的直线可设为$$y = kx + 1$$。与抛物线$$y^2 = x$$联立,得$$k^2x^2 + (2k - 1)x + 1 = 0$$。要求唯一交点,判别式$$\Delta = 0$$或$$k = 0$$(此时为水平线$$y = 1$$,与抛物线相切)。解得$$k = 0$$或$$k = \frac{1}{4}$$,另外还有一条垂直线$$x = 0$$也与抛物线有唯一交点。共3条。答案为$$B$$。
8. 直线$$3x - y + 1 = 0$$的斜率为$$3$$。答案为$$A$$。
9. 题目中直线方程未显示完整,无法解析。
10. 直线$$y = kx + b$$经过第二、三、四象限,说明斜率$$k < 0$$且截距$$b < 0$$。答案为$$B$$。
.jpg)