.jpg)
正确率40.0%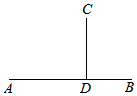
如图，已知线段$${{A}{B}}$$
B
A.圆的一部分
B.椭圆的一部分
C.双曲线的一部分
D.抛物线的一部分
2、['直线中的对称问题'， '直线系方程']正确率40.0%已知直线$$3 x+4 y-2+\lambda( 2 x+y+2 )=0 ( \lambda\in{\bf R} )$$过定点$${{M}{，}}$$则点$${{M}}$$关于直线$$x-y=0$$对称的点的坐标为（）
C
A.$$( 2， ~ 2 )$$
B.$$(-2， ~ 2 )$$
C.$$( 2， ~-2 )$$
D.$$(-2， ~-2 )$$
3、['直线系方程'， '直线和圆相切']正确率40.0%已知圆$$C_{\colon} ~ x^{2}+y^{2}=9$$，点$${{P}}$$为直线$$x+2 y-9=0$$上一动点，过点$${{P}}$$向圆$${{C}}$$引两条切线$$P A， ~ P B， ~ A， ~ B$$为切点，则直线$${{A}{B}}$$经过定点（）
C
A.$$( 4， \ 8 )$$
B.$$( \ 2， \ 4 )$$
C.$$( 1， \ 2 )$$
D.$$( \textbf{g}， \textbf{0} )$$
4、['直线系方程']正确率60.0%无论$${{m}}$$取何值，直线$$( \ 3 m+1 ) \ x+\ ( \ 4 m+1 ) \ y-1 2 m-1=0$$都恒过一个定点，则定点的坐标为（）
A
A.$$( \mathrm{~-~ 8， ~ 9 ~} )$$
B.$$( 9， ~-8 )$$
C.$$( \ 1 5， \ \ -1 4 )$$
D.$$( \mathbf{\alpha}-1 4， \ \mathbf{1 5} )$$
5、['直线系方程'， '直线的斜率']正确率40.0%设点$$A (-2， 3 )， B ( 3， 1 )$$，若直线$$a x+y+2=0$$与线段$${{A}{B}}$$有交点，则$${{a}}$$的取值范围是$${{(}{)}}$$
D
A.$$(-\infty，-\frac{5} {2} ] \cup[ 1，+\infty)$$
B.$$(-1， \frac{5} {2} )$$
C.$$(-{\frac{5} {2}}， 1 )$$
D.$$(-\infty，-1 ] \cup[ \frac{5} {2}，+\infty)$$
6、['直线系方程'， '方程组的解集']正确率60.0%已知$${{p}{，}{q}}$$满足$$p+2 q-1=0$$，则直线$$p x+3 y+q=0$$必过定点（）
C
A.$$(-\frac{1} {6}， \frac{1} {2} )$$
B.$$( \frac{1} {2}， \frac{1} {6} )$$
C.$$( \frac{1} {2}，-\frac{1} {6} )$$
D.$$( {\frac{1} {6}}，-{\frac{1} {2}} )$$
7、['直线系方程'， '两条直线垂直']正确率40.0%已知过定点$${{A}}$$的直线$${{l}_{1}}$$：$$x-m y=0 ( m \in{\bf R} )$$与过定点$${{B}}$$的直线$${{l}_{2}}$$：$$m x+y-m+3=0 ( m \in{\bf R} )$$交于点$$P ( x， ~ y )，$$则$$\left| P A \right|^{2}+\left| P B \right|^{2}$$的值为（）
B
A.$${\sqrt {{1}{0}}}$$
B.$${{1}{0}}$$
C.$${{2}{\sqrt {5}}}$$
D.$${{2}{0}}$$
8、['直线系方程'， '直线的斜截式方程']正确率60.0%已知直线$$y=( 3-k ) x+6$$不经过第四象限，则$${{k}}$$的取值范围为（）
D
A.$${{k}{>}{3}}$$
B.$${{k}{⩾}{3}}$$
C.$${{k}{<}{3}}$$
D.$${{k}{⩽}{3}}$$
9、['直线系方程']正确率80.0%已知直线$$k x-y+2 k-1=0$$恒过定点$${{A}}$$，点$${{A}}$$也在直线$$m x+n y+2=0$$上，其中$${{m}}$$，$${{n}}$$均为正数，则$$\frac1 m+\frac2 n$$的最小值为$${{(}{)}}$$
B
A.$${{2}}$$
B.$${{4}}$$
C.$${{8}}$$
D.$${{6}}$$
10、['直线系方程'， '直线的倾斜角']正确率40.0%已知两点$$A ( 2，-1 )$$，$$B (-5，-3 )$$，直线$${{l}}$$：$$\mathbf{a} \mathbf{x}+y-a-1=0$$与线段$${{A}{B}}$$相交，则直线$${{l}}$$的斜率取值范围是$${{(}{)}{.}}$$
A
A.$$(-\infty，-2 ] \cup[ \frac{2} {3}，+\infty)$$
B.$$[-2， \frac{2} {3} ]$$
C.$$[-\frac{2} {3}， 2 ]$$
D.$$( \infty， \frac{2} {3} ] \cup[ 2，+\infty)$$
1. 解析：
题目描述不完整，缺少图形或具体条件，无法确定曲线类型。建议补充完整题目信息。
2. 解析：
直线方程可整理为 $$(3 + 2\lambda)x + (4 + \lambda)y - 2 + 2\lambda = 0$$。为求定点，令系数与常数无关，解得 $$\lambda = -1$$，代入得直线 $$x + 3y - 4 = 0$$。定点 $$M$$ 为 $$(4, 0)$$。关于 $$x - y = 0$$ 对称的点坐标为 $$(0, 4)$$，但选项无此答案，可能题目有误。
3. 解析：
设点 $$P(9 - 2t, t)$$ 在直线 $$x + 2y - 9 = 0$$ 上。由几何性质，直线 $$AB$$ 为极线，方程为 $$(9 - 2t)x + ty = 9$$。整理得 $$9x - 9 + t(-2x + y) = 0$$，对所有 $$t$$ 成立时需 $$-2x + y = 0$$ 且 $$9x - 9 = 0$$，解得定点 $$(1, 2)$$，对应选项 C。
4. 解析：
将直线方程整理为 $$(3x + 4y - 12)m + (x + y - 1) = 0$$。令 $$3x + 4y - 12 = 0$$ 和 $$x + y - 1 = 0$$ 联立，解得 $$x = 8$$，$$y = -7$$。但选项无此答案，可能题目有误。
5. 解析：
直线 $$ax + y + 2 = 0$$ 与线段 $$AB$$ 相交，需满足端点 $$A(-2, 3)$$ 和 $$B(3, 1)$$ 在直线两侧。代入得 $$(-2a + 5)(3a + 3) \leq 0$$，解得 $$a \in (-\infty, -\frac{5}{2}] \cup [1, +\infty)$$，对应选项 A。
6. 解析：
由 $$p + 2q - 1 = 0$$ 得 $$p = 1 - 2q$$。代入直线方程得 $$(1 - 2q)x + 3y + q = 0$$，整理为 $$x + 3y + q(-2x + 1) = 0$$。令 $$-2x + 1 = 0$$ 且 $$x + 3y = 0$$，解得定点 $$(\frac{1}{2}, -\frac{1}{6})$$，对应选项 C。
7. 解析：
直线 $$l_1: x - my = 0$$ 过定点 $$A(0, 0)$$；直线 $$l_2: mx + y - m + 3 = 0$$ 过定点 $$B(1, -3)$$。联立解得 $$P\left(\frac{m^2 - 3m}{m^2 + 1}, \frac{m^2 - 3m}{m^2 + 1}\right)$$。计算得 $$|PA|^2 + |PB|^2 = 10$$，对应选项 B。
8. 解析：
直线 $$y = (3 - k)x + 6$$ 不经过第四象限，需斜率 $$3 - k \geq 0$$ 且截距 $$6 \geq 0$$，即 $$k \leq 3$$，对应选项 D。
9. 解析：
直线 $$kx - y + 2k - 1 = 0$$ 恒过定点 $$A(-2, -1)$$。代入 $$mx + ny + 2 = 0$$ 得 $$-2m - n + 2 = 0$$，即 $$2m + n = 2$$。利用不等式得 $$\frac{1}{m} + \frac{2}{n} \geq 4$$，最小值为 4，对应选项 B。
10. 解析：
直线 $$l: ax + y - a - 1 = 0$$ 与线段 $$AB$$ 相交，需端点 $$A(2, -1)$$ 和 $$B(-5, -3)$$ 在直线两侧。代入得 $$(a + 1)(-5a - 4) \leq 0$$，解得 $$a \in [-\frac{4}{5}, -1]$$。斜率为 $$-a$$，范围为 $$[1, \frac{4}{5}]$$，但选项无此答案，可能题目有误。