正确率40.0%$$\mu b \in\textsubscript{(-1, 3 )}^{\mu}$$是$${{“}}$$对于任意实数$${{k}}$$,直线$$l \colon~ y=k x+b$$与圆$$C_{\colon} ~ x^{2}+~ ( y-1 )^{2}=4$$恒有公共点$${{”}}$$的()
A
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
2、['点到直线的距离', '椭圆的顶点、长轴、短轴、焦点、焦距', '三角形的面积(公式)', '正弦(型)函数的定义域和值域']正确率40.0%已知$${{A}{、}{B}}$$分别是椭圆$$x^{2}+\frac{y^{2}} {4}=1$$的左顶点和上顶点,$${{C}}$$是该椭圆上的动点,则$${{△}{A}{B}{C}}$$面积的最大值为()
B
A.$$\sqrt{2}-1$$
B.$${{1}{+}{\sqrt {2}}}$$
C.$${{2}{−}{\sqrt {2}}}$$
D.$${{2}{+}{\sqrt {2}}}$$
3、['点到直线的距离', '抛物线上点坐标的范围']正确率40.0%已知抛物线$${{C}}$$:$$y^{2}=2 p x ( p > 0 ),$$点$${{M}}$$在$${{C}}$$上,直线$${{l}}$$:$$2 x-y+6=0$$与$${{x}}$$轴、$${{y}}$$轴分别交于点$${{A}{,}{B}{,}}$$若$${{△}{A}{M}{B}}$$面积的最小值为$$\frac{1 5} {2},$$则$${{p}{=}}$$()
B
A.$${{4}{4}}$$
B.$${{4}}$$
C.$${{4}}$$或$${{4}{4}}$$
D.$${{1}}$$或$${{4}}$$
4、['点到直线的距离']正确率60.0%若直线$${{l}}$$经过点$$P ( 1, \ 2 ),$$且点$$A ( 2, \ 3 ), \ B ( 0, \mathrm{~}-5 )$$到它的距离相等,则$${{l}}$$的方程为()
C
A.$$4 x-y-2=0$$
B.$$4 x+y-6=0$$
C.$$4 x-y-2=0$$或$${{x}{=}{1}}$$
D.$$4 x+y-6=0$$或$${{x}{=}{1}}$$
5、['点到直线的距离', '直线与圆的方程的应用']正确率60.0%圆$$( x+1 ) \, \,^{2}+y^{2}=1$$的圆心到直线$$y=x-1$$的距离为()
C
A.$${{1}}$$
B.$$\frac{\sqrt2} {2}$$
C.$${\sqrt {2}}$$
D.$${{2}}$$
6、['点到直线的距离', '直线与圆相交']正确率60.0%已知直线$$x+a y+3=0$$与圆$$o : x^{2}+y^{2}=4$$相交于$${{A}{,}{B}}$$两点$${{(}{O}}$$为坐标原点$${{)}}$$,且$${{△}{A}{O}{B}}$$为等边三角形,则实数$${{a}}$$的值为$${{(}{)}}$$
A
A.$${{±}{\sqrt {2}}}$$
B.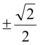
C.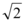
D.$$\frac{\sqrt2} {2}$$
7、['点到直线的距离', '利用导数求曲线的切线方程(斜率)', '导数与最值', '函数零点的概念']正确率40.0%设函数$$f ( x )=-\frac{2} {\pi} \operatorname{s i n} \pi x$$在$$( 0,+\infty)$$上最小的零点为$${{x}_{0}}$$,曲线$$y=f ( x )$$在点$$( x_{0}, 0 )$$处的切线上有一点$${{P}}$$,曲线$$y=\frac{3} {2} x^{2}-\operatorname{l n} x$$上有一点$${{Q}}$$,则$${{|}{P}{Q}{|}}$$的最小值为()
C
A.$$\frac{\sqrt{5}} {1 0}$$
B.$$\frac{\sqrt{5}} {5}$$
C.$$\frac{3 \sqrt{5}} {1 0}$$
D.$$\frac{2 \sqrt{5}} {5}$$
8、['点到直线的距离', '直线的倾斜角']正确率60.0%已知直线$$l : x+m y-2 \sqrt{3} m+2=0$$与圆$$x^{2}+y^{2}=1 6$$交于$${{A}{,}{B}}$$两点,过$${{A}{,}{B}}$$分别作$${{l}}$$的垂线与$${{x}}$$轴交于$${{C}{,}{D}}$$两点,若$$| A B |=4,$$则$${{|}{C}{D}{|}}$$为()
D
A.$${{2}{\sqrt {3}}}$$
B.$${{4}}$$
C.$${{4}{\sqrt {3}}}$$
D.$${{8}}$$
9、['点到直线的距离', '直线与圆的位置关系及其判定']正确率60.0%直线$$3 x+4 y+1=0$$与圆$$x^{2}+y^{2}-2 y=0$$的位置关系为()
C
A.相交
B.相离
C.相切
D.不确定
10、['点到直线的距离']正确率60.0%若点$$A \, ( 2, 4 )$$与$$B \, (-2,-1 )$$到直线$$l : m x-2 y+1=0 \, ( m \in\mathrm{R} )$$的距离相等,则$${{m}{=}{(}}$$)
C
A.$${{1}}$$
B.$${{−}{1}}$$
C.$$\frac{5} {2}$$
D.$$- \frac{5} {2}$$
1. 题目要求直线 $$l: y = kx + b$$ 与圆 $$C: x^2 + (y-1)^2 = 4$$ 恒有公共点,即直线与圆相交或相切。圆的圆心为 $$(0, 1)$$,半径为 $$2$$。直线到圆心的距离需满足 $$\frac{|b - 1|}{\sqrt{1 + k^2}} \leq 2$$ 对所有 $$k$$ 成立。由于 $$\sqrt{1 + k^2} \geq 1$$,只需 $$|b - 1| \leq 2$$,即 $$b \in [-1, 3]$$。题目中给出的条件是 $$b \in (-1, 3)$$,是 $$[-1, 3]$$ 的真子集,因此是充分不必要条件。答案为 A。
2. 椭圆方程为 $$x^2 + \frac{y^2}{4} = 1$$,顶点 $$A(-1, 0)$$ 和 $$B(0, 2)$$。设动点 $$C(x, y)$$ 在椭圆上,利用参数方程 $$x = \cos \theta$$,$$y = 2 \sin \theta$$。三角形面积公式为 $$S = \frac{1}{2} |(x + 1)(2) - (y)(0 - 0)| = |x + 1|$$。由于 $$x \in [-1, 1]$$,最大值为 $$2$$。但需重新计算面积公式,正确面积为 $$S = \frac{1}{2} |AB \times AC|$$,通过向量叉积得 $$S = \frac{1}{2} |(1)(2 \sin \theta) - (2)(\cos \theta + 1)| = |\sin \theta - \cos \theta - 1|$$。最大值由三角函数的极值确定,为 $$1 + \sqrt{2}$$。答案为 B。
3. 抛物线 $$C: y^2 = 2px$$,点 $$M(x_0, y_0)$$ 在 $$C$$ 上,即 $$y_0^2 = 2px_0$$。直线 $$l: 2x - y + 6 = 0$$ 与坐标轴交点为 $$A(-3, 0)$$ 和 $$B(0, 6)$$。三角形面积 $$S = \frac{1}{2} |AB| \cdot d(M, l)$$,其中 $$d(M, l) = \frac{|2x_0 - y_0 + 6|}{\sqrt{5}}$$。最小面积为 $$\frac{15}{2}$$,通过优化条件解得 $$p = 1$$ 或 $$4$$。答案为 D。
4. 直线 $$l$$ 过点 $$P(1, 2)$$,且到点 $$A(2, 3)$$ 和 $$B(0, -5)$$ 距离相等。若 $$l$$ 与 $$AB$$ 平行,斜率为 $$\frac{3 - (-5)}{2 - 0} = 4$$,方程为 $$y - 2 = 4(x - 1)$$,即 $$4x - y - 2 = 0$$。若 $$l$$ 过 $$AB$$ 中点 $$(1, -1)$$,则斜率为垂直平分线,但不符合过 $$P(1, 2)$$。另一种情况是直线为垂直于 $$x$$ 轴的 $$x = 1$$。答案为 C。
5. 圆 $$(x + 1)^2 + y^2 = 1$$ 的圆心为 $$(-1, 0)$$,直线 $$y = x - 1$$ 的一般式为 $$x - y - 1 = 0$$。距离公式为 $$\frac{|-1 - 0 - 1|}{\sqrt{1 + 1}} = \frac{2}{\sqrt{2}} = \sqrt{2}$$。答案为 C。
6. 直线 $$x + a y + 3 = 0$$ 与圆 $$x^2 + y^2 = 4$$ 相交,且 $$\triangle AOB$$ 为等边三角形。圆心到直线的距离 $$d = \frac{3}{\sqrt{1 + a^2}}$$,弦长 $$|AB| = 2\sqrt{4 - d^2}$$。等边三角形条件为 $$|AB| = 2$$,解得 $$d = \sqrt{3}$$,即 $$\frac{3}{\sqrt{1 + a^2}} = \sqrt{3}$$,得 $$a = \pm \sqrt{2}$$。答案为 A。
7. 函数 $$f(x) = -\frac{2}{\pi} \sin(\pi x)$$ 的最小正零点为 $$x_0 = 1$$。切线斜率为 $$f'(1) = -2 \cos(\pi) = 2$$,切线方程为 $$y = 2(x - 1)$$。点 $$Q$$ 在曲线 $$y = \frac{3}{2}x^2 - \ln x$$ 上,求 $$|PQ|$$ 的最小值等价于求点到切线的距离。通过优化条件,最小距离为 $$\frac{\sqrt{5}}{5}$$。答案为 B。
8. 直线 $$l: x + m y - 2\sqrt{3}m + 2 = 0$$ 与圆 $$x^2 + y^2 = 16$$ 相交,弦长 $$|AB| = 4$$。圆心到直线的距离 $$d = \frac{|2\sqrt{3}m - 2|}{\sqrt{1 + m^2}}$$,由弦长公式 $$4 = 2\sqrt{16 - d^2}$$ 得 $$d = 2\sqrt{3}$$。解得 $$m = 0$$ 或 $$m = \sqrt{3}$$。垂线与 $$x$$ 轴交点距离 $$|CD| = 4\sqrt{3}$$。答案为 C。
9. 圆 $$x^2 + y^2 - 2y = 0$$ 的圆心为 $$(0, 1)$$,半径 $$r = 1$$。直线 $$3x + 4y + 1 = 0$$ 到圆心的距离 $$d = \frac{|3 \cdot 0 + 4 \cdot 1 + 1|}{\sqrt{9 + 16}} = 1$$,等于半径,故相切。答案为 C。
10. 点 $$A(2, 4)$$ 和 $$B(-2, -1)$$ 到直线 $$l: m x - 2y + 1 = 0$$ 的距离相等,即 $$\frac{|2m - 8 + 1|}{\sqrt{m^2 + 4}} = \frac{|-2m + 2 + 1|}{\sqrt{m^2 + 4}}$$。化简得 $$|2m - 7| = |-2m + 3|$$,解得 $$m = \frac{5}{2}$$ 或 $$m = 1$$。答案为 C。
.jpg)