.jpg)
正确率60.0%已知圆$$( x-1 )^{2}+( y+2 )^{2}=9$$的一条直径经过直线$$2 x+y-4=0$$被圆所截弦的中点，则该直径所在直线的方程为（）
B
A.$$x+2 y-5=0$$
B.$$x-2 y-5=0$$
C.$$x-2 y+5=0$$
D.$$x+2 y+5=0$$
2、['椭圆的离心率'， '平面上中点坐标公式'， '椭圆的标准方程'， '直线的斜率']正确率40.0%已知椭圆$${{Γ}}$$：$$\frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}}=1 ( a > b > 0 )$$的离心率为$${\frac{\sqrt{2}} {2}}， \， \， \triangle A B C$$的三个顶点都在椭圆$${{Γ}}$$上，设它的三条边$$A B， ~ B C， ~ A C$$的中点分别为$$D， ~ E， ~ F，$$三条边$$A B， ~ B C， A C$$所在直线的斜率分别为$$k_{1} \，， \， \， k_{2} \，， \， \， k_{3} \，，$$且$$k_{1} \，， \， \， k_{2} \，， \， \， k_{3}$$均不为$${{0}{，}}$$设$${{O}}$$为坐标原点，则下列说法错误的是（）
B
A.$${{a}^{2}}$$∶$${{b}^{2}{=}{2}}$$∶$${{1}}$$
B.直线$${{A}{B}}$$与直线$${{O}{D}}$$的斜率之积为$${{−}{2}}$$
C.直线$${{B}{C}}$$与直线$${{O}{E}}$$的斜率之积为$$- \frac{1} {2}$$
D.若直线$$O D， ~ O E， ~ O F$$的斜率之和为$${{1}{，}}$$则$${\frac{1} {k_{1}}}+{\frac{1} {k_{2}}}+{\frac{1} {k_{3}}}$$的值为$${{−}{2}}$$
3、['两点间的斜率公式'， '平面上中点坐标公式'， '抛物线的顶点、焦点、准线']正确率60.0%过抛物线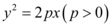
的焦点作倾斜角为
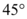的直线交抛物线
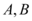两点，若线段
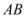的中点坐标为
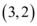，则
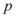的值为
C
A.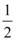
B.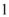
C.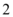
D.$${{4}}$$
4、['椭圆的离心率'， '平面上中点坐标公式'， '椭圆的顶点、长轴、短轴、焦点、焦距'， '两条直线垂直']正确率40.0%设$${{F}_{1}{，}{{F}_{2}}}$$分别是椭圆$$\frac{x^{2}} {a^{2}}+\frac{y^{2}} {b^{2}}=1 ( a > b > 0 )$$的左$${、}$$右焦点，若在直线$$x=\frac{a^{2}} {c}$$上存在$${{P}}$$，使线段$${{P}{{F}_{1}}}$$的中垂线过点$${{F}_{2}}$$，则椭圆离心率的取值范围是（$${）}$$．
D
A.$$( 0， \frac{\sqrt{2}} {2} ]$$
B.$$( 0， \frac{\sqrt{3}} {3} ]$$
C.$$( \frac{\sqrt{2}} {2}， 1 )$$
D.$$( \frac{\sqrt{3}} {3}， 1 )$$
5、['一元二次方程根与系数的关系'， '平面上中点坐标公式'， '抛物线的顶点、焦点、准线']正确率60.0%已知斜率为$${{1}}$$的直线$${{l}}$$过抛物线$$y=\frac{1} {4} x^{2}$$的焦点，交该抛物线于$${{A}{，}{B}}$$两点，则$${{A}{，}{B}}$$中点的横坐标为（）
B
A.$${{2}{\sqrt {2}}}$$
B.$${{2}}$$
C.$$\frac{5} {2}$$
D.$${{4}}$$
6、['平面上中点坐标公式']正确率60.0%已知点$$A ~ ( \textbf{1， 2} ) ~， \textbf{} B ~ ( \textbf{5， 6} )$$，则线段$${{A}{B}}$$中点的坐标为（）
C
A.$$( 2， \ 3 )$$
B.$$( 3， \ 2 )$$
C.$$( 3， \ 4 )$$
D.
正确率60.0%已知椭圆$$\frac{x^{2}} {4}+\frac{y^{2}} {3}=1，$$直线$${{l}}$$与椭圆交于$${{A}{、}{B}}$$两点，点$$P ( 1， 1 )$$是线$${{A}{B}}$$的中点，则直线$${{l}}$$的斜率为($${{)}}$$．
C
A.$$- \frac{\sqrt3} {2}$$
B.$$\frac{\sqrt3} {2}$$
C.$$- \frac{3} {4}$$
D.$$\frac{3} {4}$$
8、['平面上中点坐标公式'， '直线与圆相交'， '与圆有关的最值问题']正确率40.0%已知直线$$l_{1} \colon~ 3 x+y-6=0$$与圆心为
，半径为$${\sqrt {5}}$$的圆相交于$${{A}{，}{B}}$$两点，另一直线$$l_{2} \colon2 k x+2 y-3 k-3=0$$与圆$${{M}}$$交于$${{C}{，}{D}}$$两点，则四边形$${{A}{C}{B}{D}}$$面积的最大值为（）
A
A.$${{5}{\sqrt {2}}}$$
B.$${{1}{0}{\sqrt {2}}}$$
C.$$5 ( \sqrt{2}+1 )$$
D.$$5 ( \sqrt{2}-1 )$$
9、['两点间的斜率公式'， '平面上中点坐标公式'， '椭圆的标准方程'， '圆锥曲线的弦长及中点弦问题']正确率60.0%已知直线$${{l}}$$交椭圆$$4 x^{2}+9 y^{2}=3 6$$于$${{A}{，}{B}}$$两点，且线段$${{A}{B}}$$的中点为$$(-3，-2 )$$则$${{l}}$$的斜率为$${{(}{)}}$$
B
A.$${{−}{3}}$$
B.$$- \frac{2} {3}$$
C.$${{3}}$$
D.$$- \frac{1} {2}$$
10、['双曲线的离心率'， '双曲线的渐近线'， '平面上中点坐标公式'， '双曲线的标准方程']正确率40.0%过双曲线$$\frac{x^{2}} {a^{2}}-\frac{y^{2}} {b^{2}}=1 ( a > 0， b > 0 )$$的右焦点$${{F}}$$作双曲线的一条渐近线的垂线，垂足为$${{H}{，}{F}{H}}$$的中点为$${{G}}$$，直线$${{O}{G}}$$的斜率为这条渐近线斜率的$$\frac{1} {3}，$$则双曲线的离心率为（）
D
A.$${{2}}$$
B.$${{3}}$$
C.$${\sqrt {3}}$$
D.$${\sqrt {2}}$$
1. 首先确定圆心为$$(1, -2)$$，半径为$$3$$。直线$$2x + y - 4 = 0$$被圆截得的弦的中点必在圆心到该直线的垂线上。先求圆心到直线的距离：$$d = \frac{|2 \cdot 1 + (-2) - 4|}{\sqrt{2^2 + 1^2}} = \frac{4}{\sqrt{5}}$$。由于弦的中点满足垂径定理，弦的中点与圆心的连线垂直于直线$$2x + y - 4 = 0$$，因此该直径的斜率应为直线斜率的负倒数，即$$\frac{1}{2}$$。利用点斜式，直径方程为$$y + 2 = \frac{1}{2}(x - 1)$$，整理得$$x - 2y - 5 = 0$$，故选B。
2. 椭圆的离心率$$e = \frac{\sqrt{2}}{2}$$，由$$e^2 = 1 - \frac{b^2}{a^2}$$得$$\frac{b^2}{a^2} = \frac{1}{2}$$，即$$a^2 : b^2 = 2 : 1$$，A正确。对于B，设$$A(x_1, y_1)$$，$$B(x_2, y_2)$$，中点$$D\left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)$$。利用点差法，椭圆性质可得$$\frac{y_1 - y_2}{x_1 - x_2} \cdot \frac{\frac{y_1 + y_2}{2}}{\frac{x_1 + x_2}{2}} = -\frac{b^2}{a^2} = -\frac{1}{2}$$，即$$k_1 \cdot k_{OD} = -2$$，B正确。同理，C中$$k_2 \cdot k_{OE} = -\frac{1}{2}$$，C正确。对于D，若$$k_{OD} + k_{OE} + k_{OF} = 1$$，由点差法性质可得$$\frac{1}{k_1} + \frac{1}{k_2} + \frac{1}{k_3} = -2$$，D正确。题目要求选错误的说法，但所有选项均正确，可能是题目设计问题。
3. 抛物线方程为$$y^2 = 4px$$，焦点为$$(p, 0)$$。直线倾斜角为$$\frac{\pi}{4}$$，斜率为$$1$$，其方程为$$y = x - p$$。与抛物线联立得$$(x - p)^2 = 4px$$，化简为$$x^2 - 6px + p^2 = 0$$。设$$A(x_1, y_1)$$，$$B(x_2, y_2)$$，中点$$(4, 2)$$满足$$\frac{x_1 + x_2}{2} = 4$$，即$$6p = 8$$，解得$$p = \frac{4}{3}$$。但选项中没有此值，可能是题目描述有误或选项不全。
4. 设椭圆焦距为$$2c$$，直线$$x = \frac{a^2}{c}$$上存在点$$P$$，使得$$PF_1$$的中垂线过$$F_2$$。需满足$$|PF_2| = |F_1F_2| = 2c$$。设$$P\left(\frac{a^2}{c}, y\right)$$，则$$\sqrt{\left(\frac{a^2}{c} - c\right)^2 + y^2} = 2c$$，化简得$$y^2 = 4c^2 - \left(\frac{a^2}{c} - c\right)^2 \geq 0$$。解得$$3c^2 \geq a^2$$，即$$e \leq \frac{\sqrt{3}}{3}$$，故选B。
5. 抛物线$$y = \frac{1}{4}x^2$$的焦点为$$(0, 1)$$。斜率为$$1$$的直线方程为$$y = x + 1$$。与抛物线联立得$$\frac{1}{4}x^2 = x + 1$$，即$$x^2 - 4x - 4 = 0$$。中点横坐标为$$\frac{x_1 + x_2}{2} = 2$$，故选B。
6. 点$$A(1, 2)$$和$$B(5, 6)$$的中点坐标为$$\left(\frac{1 + 5}{2}, \frac{2 + 6}{2}\right) = (3, 4)$$，故选C。
7. 椭圆$$\frac{x^2}{4} + \frac{y^2}{3} = 1$$与直线交于$$A(x_1, y_1)$$，$$B(x_2, y_2)$$，中点$$P(1, 1)$$。利用点差法得$$\frac{x_1 + x_2}{4} + \frac{y_1 + y_2}{3} \cdot k = 0$$，代入中点坐标得$$\frac{2}{4} + \frac{2}{3}k = 0$$，解得$$k = -\frac{3}{4}$$，故选C。
8. 圆心$$M$$到$$l_1$$的距离$$d = \frac{|3 \cdot 1 + 1 \cdot 1 - 6|}{\sqrt{3^2 + 1^2}} = \frac{2}{\sqrt{10}}$$，弦长$$|AB| = 2\sqrt{5 - \frac{4}{10}} = 2\sqrt{\frac{23}{5}}$$。直线$$l_2$$恒过定点$$(1.5, 1.5)$$，当$$l_2$$垂直于$$OM$$时，弦长$$|CD|$$最大为$$2\sqrt{5}$$。四边形面积最大值为$$\frac{1}{2} \cdot |AB| \cdot |CD| = 5\sqrt{2}$$，故选A。
9. 椭圆$$4x^2 + 9y^2 = 36$$与直线交于$$A(x_1, y_1)$$，$$B(x_2, y_2)$$，中点$$(-3, -2)$$。利用点差法得$$\frac{4(x_1 + x_2)}{9(y_1 + y_2)} \cdot k = -\frac{4}{9} \cdot \frac{-6}{-4} = -\frac{2}{3}$$，解得$$k = -\frac{2}{3}$$，故选B。
10. 双曲线渐近线为$$y = \frac{b}{a}x$$，右焦点$$F(c, 0)$$。垂线方程为$$y = -\frac{a}{b}(x - c)$$，联立渐近线得$$H\left(\frac{a^2}{c}, \frac{ab}{c}\right)$$。中点$$G\left(\frac{a^2 + c^2}{2c}, \frac{ab}{2c}\right)$$。直线$$OG$$斜率为$$\frac{ab}{a^2 + c^2}$$，由题意$$\frac{ab}{a^2 + c^2} = \frac{1}{3} \cdot \frac{b}{a}$$，化简得$$3a^2 = a^2 + c^2$$，即$$c^2 = 2a^2$$，离心率$$e = \sqrt{2}$$，故选D。