.jpg)
正确率60.0%已知直线$${{l}_{1}}$$：$$3 x-y+3=0$$与$${{l}_{2}}$$：$$3 x-y+C=0$$之间的距离为$${\sqrt {{1}{0}}{，}}$$则$${{C}{=}}$$（）
B
A.$${{1}{3}}$$
B.$${{1}{3}}$$或$${{−}{7}}$$
C.$${{7}}$$
D.$${{7}}$$或$${{−}{{1}{3}}}$$
2、['两条平行直线间的距离'， '两条直线平行']正确率60.0%已知直线$$l_{1} \colon~ 3 x+4 y+5=0$$与直线$$l_{2} \colon~ 6 x+b y=0$$平行，且$${{l}_{1}}$$与$${{l}_{2}}$$之间的距离等于
A
A.$${{1}}$$
B.$${{2}}$$
C.$${\sqrt {5}}$$
D.$${{5}}$$
3、['两条平行直线间的距离']正确率80.0%两条平行直线线$$3 x+4 y-9=0$$和$$6 x+8 y+2=0$$的距离是（）
B
A.
B.$${{2}}$$
C.$$\frac{1 1} {5}$$
D.$$\frac{7} {5}$$
4、['两条平行直线间的距离'， '直线的一般式方程及应用']正确率60.0%若直线$${{l}_{1}}$$：$$x+3 y+m=0 ( m > 0 )$$与直线$${{l}_{2}}$$：$$2 x+6 y-3=0$$的距离为$${\sqrt {{1}{0}}{，}}$$则$${{m}{=}}$$（）
B
A.$${{7}}$$
B.$$\frac{1 7} {2}$$
C.$${{1}{4}}$$
D.$${{1}{7}}$$
5、['古典概型的概率计算公式'， '古典概型的应用'， '两条平行直线间的距离']正确率40.0%从集合$$\{-1， 2， 3 \}$$中随机抽取一个数$${{a}}$$，从集合$$\{-2， 4， 6， 7 \}$$中随机抽取一个数$${{b}}$$，则点$$( a， b )$$落在平行直线$$2 x-y-2=0$$与$$2 x-y+3=0$$内(不包括两条平行直线)的概率为$${{(}{)}}$$
D
A.$$\frac{7} {1 2}$$
B.$$\frac{1} {4}$$
C.$$\frac{1} {2}$$
D.$$\frac{5} {1 2}$$
6、['两条平行直线间的距离']正确率60.0%已知直线$$\l_{1} \colon~ x+a y-1=0$$与$$l_{2} \colon~ 2 x-y+1=0$$平行，则$${{l}_{1}}$$与$${{l}_{2}}$$的距离为$${{(}{)}}$$
D
A.$$\frac{1} {5}$$
B.$$\frac{\sqrt{5}} {5}$$
C.$$\frac{3} {5}$$
D.$$\frac{3 \sqrt{5}} {5}$$
7、['直线的截距式方程'， '两条平行直线间的距离']正确率40.0%已知直线$$l_{1} \colon m x+2 y-4-m=0 ( m > 0 )$$在$${{x}}$$轴$${、{y}}$$轴上的截距相等，则直线$${{l}_{1}}$$与直线$$\l_{2} \colon~ x+y-1=0$$间的距离为$${{(}{)}}$$
B
A.$$\frac{\sqrt2} {2}$$
B.$${\sqrt {2}}$$
C.$$\frac{\sqrt2} {2}$$或$${\sqrt {2}}$$
D.$${{0}}$$或$${\sqrt {2}}$$
8、['两条平行直线间的距离'， '两条直线平行']正确率60.0%两条平行直线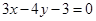
和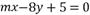
之间的距离是$${{(}{)}}$$
A
A.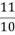
B.
C.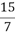
D.
正确率60.0%已知直线$$l_{1} \colon m x-3 y+6=0， \， \， l_{2} \colon\， 4 x-3 m y+1 2=0$$.若$$l_{1} / / l_{2}$$，则$${{l}_{1}{，}{{l}_{2}}}$$之间的距离为（）
A
A.$$\frac{1 2 \sqrt{1 3}} {1 3}$$
B.$$\frac{8 \sqrt{1 3}} {1 3}$$
C.$$\frac{9 \sqrt{1 3}} {1 3}$$
D.$${\sqrt {{1}{3}}}$$
10、['点到直线的距离'， '两条平行直线间的距离'， '导数的几何意义'， '两条直线平行']正确率40.0%点$${{P}}$$是曲线$$x^{2}-y-2 \operatorname{l n} \sqrt{x}=0$$上任意一点，则点$${{P}}$$到直线$$4 x+4 y+1=0$$的最小距离是$${{(}{)}}$$
B
A.$${\frac{\sqrt2} {2}} ( 1-\operatorname{l n} 2 )$$
B.$${\frac{\sqrt2} {2}} ( 1+\operatorname{l n} 2 )$$
C.$${\frac{\sqrt2} {2}} ( {\frac{1} {2}}+\operatorname{l n} 2 )$$
D.$$\frac1 2 ( 1+\operatorname{l n} 2 )$$
1. 直线距离公式为 $$\frac{|C_1 - C_2|}{\sqrt{A^2 + B^2}}$$。对于 $$l_1$$ 和 $$l_2$$，$$A=3$$，$$B=-1$$，$$C_1=3$$，$$C_2=C$$。距离为 $$\frac{|3 - C|}{\sqrt{10}} = \sqrt{10}$$，解得 $$|3 - C| = 10$$，即 $$C = 13$$ 或 $$C = -7$$。答案为 B。
2. 平行条件为 $$\frac{6}{3} = \frac{b}{4}$$，得 $$b=8$$。$$l_2$$ 为 $$6x + 8y = 0$$，即 $$3x + 4y = 0$$。距离公式为 $$\frac{|5 - 0|}{\sqrt{3^2 + 4^2}} = 1$$。答案为 A。
3. 将 $$6x + 8y + 2 = 0$$ 化简为 $$3x + 4y + 1 = 0$$。距离为 $$\frac{| -9 - 1 |}{\sqrt{3^2 + 4^2}} = \frac{10}{5} = 2$$。答案为 B。
4. 将 $$l_2$$ 化简为 $$x + 3y - \frac{3}{2} = 0$$。距离为 $$\frac{|m - (-\frac{3}{2})|}{\sqrt{1^2 + 3^2}} = \sqrt{10}$$，解得 $$|m + \frac{3}{2}| = 10$$。因 $$m > 0$$，故 $$m = \frac{17}{2}$$。答案为 B。
5. 点 $$(a, b)$$ 需满足 $$-2 < 2a - b < 3$$。总共有 $$3 \times 4 = 12$$ 种组合，满足条件的有 $$(2, -2)$$, $$(2, 4)$$, $$(2, 6)$$, $$(3, 4)$$, $$(3, 6)$$, $$(3, 7)$$, $$(-1, -2)$$，共 7 种。概率为 $$\frac{7}{12}$$。答案为 A。
6. 平行条件为 $$\frac{2}{1} = \frac{-1}{a}$$，得 $$a = -\frac{1}{2}$$。$$l_1$$ 为 $$x - \frac{1}{2}y -1 = 0$$，即 $$2x - y - 2 = 0$$。距离为 $$\frac{| -2 - 1 |}{\sqrt{2^2 + (-1)^2}} = \frac{3}{\sqrt{5}} = \frac{3\sqrt{5}}{5}$$。答案为 D。
7. 截距相等条件为 $$x=0$$ 时 $$y = \frac{4 + m}{2}$$，$$y=0$$ 时 $$x = \frac{4 + m}{m}$$。令 $$\frac{4 + m}{2} = \frac{4 + m}{m}$$，解得 $$m = 2$$。$$l_1$$ 为 $$2x + 2y - 6 = 0$$，即 $$x + y - 3 = 0$$。距离为 $$\frac{| -3 - (-1) |}{\sqrt{1^2 + 1^2}} = \sqrt{2}$$。答案为 B。
8. 将两直线化简为 $$3x + 4y - 6 = 0$$ 和 $$3x + 4y + 4 = 0$$。距离为 $$\frac{| -6 - 4 |}{\sqrt{3^2 + 4^2}} = \frac{10}{5} = 2$$。答案为 B。
9. 平行条件为 $$\frac{m}{4} = \frac{-3}{-3m}$$，得 $$m = \pm 2$$。若 $$m = 2$$，$$l_1$$ 为 $$2x - 3y + 6 = 0$$，$$l_2$$ 为 $$4x - 6y + 12 = 0$$，即 $$2x - 3y + 6 = 0$$，距离为 0（重合）。若 $$m = -2$$，$$l_1$$ 为 $$-2x - 3y + 6 = 0$$，$$l_2$$ 为 $$4x + 6y + 12 = 0$$，即 $$2x + 3y + 6 = 0$$。距离为 $$\frac{|6 - (-6)|}{\sqrt{2^2 + 3^2}} = \frac{12}{\sqrt{13}} = \frac{12\sqrt{13}}{13}$$。答案为 A。
10. 曲线化简为 $$y = x^2 - \ln x$$。设点 $$P(x, x^2 - \ln x)$$，距离为 $$\frac{|4x + 4(x^2 - \ln x) + 1|}{\sqrt{4^2 + 4^2}} = \frac{|4x^2 + 4x - 4\ln x + 1|}{4\sqrt{2}}$$。求导得极小值点为 $$x = \frac{1}{2}$$，距离为 $$\frac{\sqrt{2}}{2}(1 - \ln 2)$$。答案为 A。