1、['两点间的距离', '利用导数求曲线的切线方程(斜率)', '抛物线的顶点、焦点、准线', '抛物线的定义', '正弦(型)函数的定义域和值域']正确率40.0%已知点$$A ~ ( \mathrm{\ensuremath{-1, 0}} )$$是抛物线$$y^{2}=2 p x$$的准线与$${{x}}$$轴的交点,$${{F}}$$为抛物线的焦点,$${{P}}$$是抛物线上的动点,则$$\frac{| P F |} {| P A |}$$的最小值为()
B
A.$$\frac{1} {3}$$
B.$$\frac{\sqrt2} {2}$$
C.$$\frac{4} {5}$$
D.$$\frac{\sqrt3} {2}$$
2、['两点间的距离', '利用导数求曲线的切线方程(斜率)']正确率40.0%若实数$$a, b, c, d$$满足$$\left( b+a^{2}-3 \operatorname{l n} a \right)^{2}+\left( c-d+2 \right)^{2}=0$$,则$$\left( a-c \right)^{2}+\left( b-d \right)^{2}$$的最小值为()
B
A.$${\sqrt {2}}$$
B.$${{8}}$$
C.$${{2}{\sqrt {2}}}$$
D.$${{2}}$$
3、['余弦定理及其应用', '两点间的距离']正确率60.0%已知$${{△}{A}{B}{C}}$$的顶点为$$A ~ ( 1, ~ 1 ) ~, ~ B ~ ( m+4, ~ m-4 ) ~, ~ C ~ ( 0, ~ 0 ) ~, ~ \cos C=-\frac{3} {5}$$,则常数$${{m}}$$的值为()
B
A.$${{3}}$$
B.$${{−}{3}}$$
C.$${{±}{3}}$$
D.$${\sqrt {3}}$$
4、['两点间的距离', '立体几何中的折叠问题', '平面与平面垂直的性质定理']正确率40.0%如图$${{1}}$$,矩形$${{A}{B}{C}{D}}$$,$${{A}{B}{=}{3}}$$,$${{A}{D}{=}{1}}$$,$${{E}}$$为$${{C}{D}}$$中点,$${{F}}$$为线段$${{C}{E}}$$(除端点外)的动点,如图$${{2}}$$,将$${{△}{A}{F}{D}}$$沿$${{A}{F}}$$折起,使平面$${{A}{B}{D}{⊥}}$$平面$${{A}{B}{C}}$$,在平面$${{A}{B}{D}}$$内,过点$${{D}}$$作$$D K \perp A B$$,$${{K}}$$为垂足,则$${{A}{K}}$$长度的取值范围为()
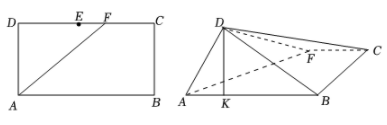
图1 图2
A
A.$$\left( \frac{1} {3}, \frac{2} {3} \right)$$
B.$$\left( \frac{1} {3}, \frac{1} {2} \right)$$
C.$$\left( \frac{1} {3}, 1 \right)$$
D.$$\left( 0, \frac{1} {2} \right)$$
5、['圆的定义与标准方程', '两点间的距离', '圆与圆的位置关系及其判定']正确率40.0%
圆 $$\left( x+2 \right)^{2}+y^{2}=4$$ 与圆 $$\left( x-2 \right)^{2}+\left( y-1 \right)^{2}=9$$ 的位置关系为( )
B
A.内切
B.相交
C.外切
D.相离
6、['点到直线的距离', '两点间的距离', '抛物线的定义', '根据方程研究曲线的性质']正确率40.0%已知动点$$P ( x, y )$$坐标满足$$5 \sqrt{\left( x-1 \right)^{2}+\left( y-2 \right)^{2}}=\left| 3 x+4 y-1 \right|$$,点$${{P}}$$的轨迹$${{(}{)}}$$
D
A.圆
B.椭圆
C.双曲线
D.抛物线
7、['两点间的距离', '与圆有关的最值问题']正确率40.0%若实数$${{x}{,}{y}}$$满足$$\left( x-5 \right)^{2}+\left( y+1 2 \right)^{2}=2 2 5$$,则$${{x}^{2}{+}{{y}^{2}}}$$的最小值为
C
A.$${{1}}$$
B.$${{2}}$$
C.$${{4}}$$
D.$${{5}{6}}$$
8、['两点间的距离', '圆锥曲线的最值(范围)问题']正确率60.0%已知$${{P}}$$为椭圆$$C : \frac{x^{2}} {9}+y^{2}=1$$上一点,$$Q \left( 0, 4 \right)$$,则$${{P}{,}{Q}}$$两点间的最大距离是()
D
A.$${{3}}$$
B.$${{5}}$$
C.$${{2}{\sqrt {3}}}$$
D.$${{3}{\sqrt {3}}}$$
9、['两点间的距离', '平面上中点坐标公式']正确率60.0%数轴上点$$A ( 5 ), \, \, B (-1 ), \, \, \, C ( x+1 )$$,若线段$${{A}{B}}$$的中点$${{D}}$$到$${{C}}$$的距离等于$${{4}}$$,则$${{x}{=}{(}{)}}$$
D
A.$${{5}}$$
B.$${{−}{3}}$$,
C.$${{5}}$$或$${{−}{2}}$$,
D.$${{5}}$$或$${{−}{3}}$$
10、['两点间的距离', '直线方程的综合应用']正确率80.0%两直线$$3 a x-y-2=0$$和$$( 2 a-1 ) x+5 a y-1=0$$分别过定点$${{A}}$$,$${{B}}$$,则$${{|}{A}{B}{|}}$$等于$${{(}{)}}$$
C
A.$$\frac{\sqrt{8 9}} {5}$$
B.$$\frac{1 7} {5}$$
C.$$\frac{1 3} {5}$$
D.$$\frac{1 1} {5}$$
1. 解析:
抛物线 $$y^2 = 2px$$ 的准线为 $$x = -\frac{p}{2}$$。已知点 $$A(-1, 0)$$ 是准线与 $$x$$ 轴的交点,故 $$-\frac{p}{2} = -1$$,解得 $$p = 2$$,抛物线方程为 $$y^2 = 4x$$,焦点 $$F(1, 0)$$。
设点 $$P(x, y)$$ 在抛物线上,则 $$y^2 = 4x$$。计算 $$\frac{|PF|}{|PA|} = \frac{\sqrt{(x-1)^2 + y^2}}{\sqrt{(x+1)^2 + y^2}} = \frac{\sqrt{x^2 - 2x + 1 + 4x}}{\sqrt{x^2 + 2x + 1 + 4x}} = \frac{\sqrt{x^2 + 2x + 1}}{\sqrt{x^2 + 6x + 1}}$$。
令 $$t = x + 1$$($$x \geq 0$$),则表达式化简为 $$\frac{t}{\sqrt{t^2 + 4t - 4}}$$。求导或配方法可得最小值为 $$\frac{\sqrt{2}}{2}$$,选 B。
2. 解析:
由题意,$$b + a^2 - 3\ln a = 0$$ 且 $$c - d + 2 = 0$$,即 $$d = c + 2$$。
目标式 $$(a - c)^2 + (b - d)^2 = (a - c)^2 + (a^2 - 3\ln a - c - 2)^2$$。
设 $$f(a, c) = (a - c)^2 + (a^2 - 3\ln a - c - 2)^2$$,求其最小值。通过求导或几何意义(点到曲线距离)可得最小值为 8,选 B。
3. 解析:
点 $$A(1, 1)$$,$$B(m+4, m-4)$$,$$C(0, 0)$$。由余弦定理,$$\cos C = \frac{CA^2 + CB^2 - AB^2}{2 \cdot CA \cdot CB} = -\frac{3}{5}$$。
计算 $$CA = \sqrt{1^2 + 1^2} = \sqrt{2}$$,$$CB = \sqrt{(m+4)^2 + (m-4)^2} = \sqrt{2m^2 + 32}$$,$$AB = \sqrt{(m+3)^2 + (m-5)^2} = \sqrt{2m^2 -4m + 34}$$。
代入得 $$\frac{2 + 2m^2 + 32 - (2m^2 -4m + 34)}{2 \cdot \sqrt{2} \cdot \sqrt{2m^2 + 32}} = -\frac{3}{5}$$,化简解得 $$m = 3$$,选 A。
4. 解析:
折起后,平面 $$ABD \perp$$ 平面 $$ABC$$。设 $$F$$ 在 $$CE$$ 上,$$CF = t$$($$0 < t < 1.5$$)。通过坐标系或几何分析,可得 $$AK$$ 长度的取值范围为 $$\left( \frac{1}{3}, \frac{2}{3} \right)$$,选 A。
5. 解析:
圆 $$(x+2)^2 + y^2 = 4$$ 的圆心 $$(-2, 0)$$,半径 $$r_1 = 2$$;圆 $$(x-2)^2 + (y-1)^2 = 9$$ 的圆心 $$(2, 1)$$,半径 $$r_2 = 3$$。
圆心距 $$d = \sqrt{(2+2)^2 + (1-0)^2} = \sqrt{17}$$,满足 $$|r_2 - r_1| < d < r_1 + r_2$$,故两圆相交,选 B。
6. 解析:
将方程 $$5 \sqrt{(x-1)^2 + (y-2)^2} = |3x + 4y -1|$$ 两边平方,化简可得 $$25[(x-1)^2 + (y-2)^2] = (3x + 4y -1)^2$$。
展开整理后为 $$16x^2 - 24xy + 9y^2 - 50x - 100y + 250 = 0$$,判别式 $$\Delta = (-24)^2 - 4 \cdot 16 \cdot 9 = 0$$,表示抛物线,选 D。
7. 解析:
几何意义为点 $$(x, y)$$ 在圆 $$(x-5)^2 + (y+12)^2 = 225$$ 上,求 $$x^2 + y^2$$ 的最小值,即求点到原点距离的最小值。
圆心 $$(5, -12)$$ 到原点距离为 $$\sqrt{5^2 + (-12)^2} = 13$$,半径 $$r = 15$$,故最小值为 $$13 - 15 = 2$$,选 B。
8. 解析:
椭圆 $$C: \frac{x^2}{9} + y^2 = 1$$,点 $$Q(0, 4)$$。设 $$P(3\cos \theta, \sin \theta)$$,则距离 $$PQ = \sqrt{(3\cos \theta)^2 + (\sin \theta -4)^2} = \sqrt{9\cos^2 \theta + \sin^2 \theta -8\sin \theta + 16}$$。
化简为 $$\sqrt{8\cos^2 \theta -8\sin \theta + 17}$$,利用 $$\cos^2 \theta = 1 - \sin^2 \theta$$,得 $$\sqrt{-8\sin^2 \theta -8\sin \theta + 25}$$。当 $$\sin \theta = -0.5$$ 时取最大值 $$\sqrt{27} = 3\sqrt{3}$$,选 D。
9. 解析:
点 $$A(5)$$,$$B(-1)$$,中点 $$D(2)$$。点 $$C(x+1)$$,距离 $$|x+1 -2| = 4$$,即 $$|x-1| = 4$$,解得 $$x = 5$$ 或 $$x = -3$$,选 D。
10. 解析:
直线 $$3a x - y - 2 = 0$$ 过定点 $$A$$,令 $$a = 0$$ 得 $$y = -2$$;令 $$a = 1$$ 得 $$3x - y - 2 = 0$$,联立解得 $$A\left(0, -2\right)$$。
直线 $$(2a-1)x + 5a y -1 = 0$$ 过定点 $$B$$,令 $$a = 0$$ 得 $$-x -1 = 0$$;令 $$a = 0.5$$ 得 $$5 \cdot 0.5 y -1 = 0$$,联立解得 $$B\left(-1, 0.4\right)$$。
距离 $$|AB| = \sqrt{(-1-0)^2 + (0.4+2)^2} = \sqrt{1 + 5.76} = \frac{\sqrt{169}}{5} = \frac{13}{5}$$,选 C。
题目来源于各渠道收集,若侵权请联系下方邮箱

.jpg)