正确率60.0%经过点$$P ( 0, ~-1 )$$的直线$${{l}}$$与以$$A ( 1, ~-2 ), ~ B ( 2, ~ 1 )$$为端点的线段总有公共点,则$${{l}}$$的倾斜角的取值范围是()
D
A.$$[-1, ~ 1 ]$$
B.$$(-\infty, ~-1 ] \cup[ 1, ~+\infty)$$
C.$$[ \frac{\pi} {4}, ~ \frac{3 \pi} {4} ]$$
D.$$[ 0, \, \, \, \frac{\pi} {4} \Big] \cup[ \frac{3 \pi} {4}, \, \, \pi)$$
2、['两点间的斜率公式', '直线的方向向量与斜率的关系']正确率60.0%若经过$$A ( m, ~ 3 ), ~ B ( 1, ~ 2 )$$两点的直线的一个方向向量为$$(-3, ~-3 ),$$则$${{m}}$$等于()
A
A.$${{2}}$$
B.$${{1}}$$
C.$${{−}{1}}$$
D.$${{−}{2}}$$
3、['两点间的斜率公式']正确率60.0%已知点$$P ( 2, ~-3 ), ~ Q ( 3, 2 ),$$直线$$a x-y+2=0$$与线段$${{P}{Q}}$$相交,则$${{a}}$$的取值范围是()
C
A.$$a \geq\frac{4} {3}$$
B.$$a \leq-\frac{4} {3}$$
C.$$- \frac{5} {2} \leqslant a \leqslant0$$
D.$$a \leq-\frac{4} {3}$$或$$a \leq\frac{1} {2}$$
4、['两点间的斜率公式', '复平面内的点、复数及平面向量', '复数的模']正确率40.0%虚数$$( x-2 )+y i$$中$${{x}{,}{y}}$$均为实数,当此虚数的模为$${{1}}$$时,$$\frac{y} {x}$$的取值范围是$${{(}{)}}$$
B
A.$$[-\frac{\sqrt{3}} {3}, \frac{\sqrt{3}} {3} ]$$
B.$$[-\frac{\sqrt{3}} {3}, 0 ) \cup( 0, \frac{\sqrt{3}} {3} ]$$
C.$$[-\sqrt{3}, \sqrt{3} ]$$
D.$$[-\sqrt{3}, 0 ) \cup( 0, \sqrt{3} ]$$
5、['两点间的斜率公式', '直线的倾斜角']正确率60.0%已知点$$A ( 1, \sqrt{3} ), ~ B (-1, 3 \sqrt{3} )$$,则直线$${{A}{B}}$$的倾斜角为()
C
A.$${{6}{0}^{∘}}$$
B.$${{3}{0}^{∘}}$$
C.$${{1}{2}{0}^{∘}}$$
D.$${{1}{5}{0}^{∘}}$$
6、['两点间的斜率公式', '直线的斜率']正确率40.0%已知两点$$M ~ ( \ 2, \ \ -1 ) ~, \ \ N ~ ( \ -4, \ -2 )$$,直线$$l \colon m x+y-m-1=0$$与线段$${{M}{N}}$$相交,则直线$${{l}}$$的斜率取值范围是()
A
A.$$( \mathrm{\Phi}-\infty, \ \mathrm{\Phi}-2 \mathrm{\Upsilon} \mathrm{\Gamma} [ \frac{3} {5}, \ \mathrm{\Upsilon}+\infty)$$
B.$$[-2, ~ \frac{3} {5} ]$$
C.$$[-\frac{3} {5}, \ 2 ]$$
D.$$( \mathrm{\Phi}-\infty, \ \mathrm{\Phi}-\frac{3} {5} ] \cup[ 2, \ \mathrm{\Phi}+\infty)$$
7、['两点间的斜率公式', '两条直线平行']正确率60.0%已知经过$$A (-1, a ), ~ B ( a, 8 )$$两点的直线与直线$$2 x-y+1=0$$平行,则实数$${{a}}$$的值是$${{(}{)}}$$
B
A.$${{1}}$$
B.$${{2}}$$
C.$${{−}{1}}$$
D.$${{−}{2}}$$
8、['两点间的斜率公式', '直线中的对称问题', '平面上中点坐标公式', '抛物线的标准方程', '直线与抛物线的综合应用']正确率40.0%抛物线$${{y}{=}{2}{{x}^{2}}}$$上两点$$A ( x_{1}, y_{1} ), ~ B ( x_{2}, y_{2} )$$关于直线$$y=x+m$$对称,且$$x_{1} \cdot x_{2}=-\frac{3} {4}$$,则实数$${{m}}$$的值为()
A
A.$${{2}}$$
B.$${{2}{\sqrt {2}}}$$
C.$${{1}}$$
D.$${{4}}$$
9、['两点间的斜率公式', '一元二次不等式存在性问题', '导数的几何意义']正确率19.999999999999996%已知函数$$f ( x )=a x^{2}+( a-1 ) l n x+1 ( a < 0 )$$,设$${{A}{,}{B}}$$为函数$${{f}{(}{x}{)}}$$图象上的任意两点,若直线$${{A}{B}}$$的斜率的绝对值不小于$${{2}}$$,则实数$${{a}}$$的取值范围是()
B
A.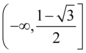
B.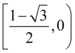
C.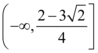
D.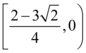
正确率40.0%已知椭圆$$C : \frac{x^{2}} {4}+y^{2}=1$$,直线$${{l}}$$交椭圆于$${{A}{,}{B}}$$两点,若$${{A}{B}}$$的中点坐标为$$(-1, \frac{1} {2} )$$,则$${{l}}$$的方程为$${{(}{)}}$$
B
A.$$4 x-2 y+5=0$$
B.$$x-2 y+2=0$$
C.$$4 x+2 y-3=0$$
D.$$x+2 y=0$$
第1题解析:
直线 $$l$$ 经过点 $$P(0, -1)$$,且与线段 $$AB$$(端点 $$A(1, -2)$$ 和 $$B(2, 1)$$)有公共点。首先计算直线 $$PA$$ 和 $$PB$$ 的斜率:
斜率 $$k_{PA} = \frac{-2 - (-1)}{1 - 0} = -1$$
斜率 $$k_{PB} = \frac{1 - (-1)}{2 - 0} = 1$$
因此,直线 $$l$$ 的斜率 $$k$$ 的取值范围为 $$[-1, 1]$$。对应的倾斜角范围为 $$[0, \frac{\pi}{4}] \cup [\frac{3\pi}{4}, \pi)$$,即选项 D。
第2题解析:
方向向量为 $$(-3, -3)$$,可以简化为 $$(1, 1)$$。因此直线的斜率为 $$1$$。根据两点 $$A(m, 3)$$ 和 $$B(1, 2)$$:
$$\frac{3 - 2}{m - 1} = 1 \Rightarrow m - 1 = 1 \Rightarrow m = 2$$
答案为 A。
第3题解析:
直线 $$ax - y + 2 = 0$$ 与线段 $$PQ$$(端点 $$P(2, -3)$$ 和 $$Q(3, 2)$$)相交。计算直线在 $$P$$ 和 $$Q$$ 处的值:
在 $$P$$ 点:$$2a - (-3) + 2 \geq 0 \Rightarrow 2a + 5 \geq 0 \Rightarrow a \geq -\frac{5}{2}$$
在 $$Q$$ 点:$$3a - 2 + 2 \leq 0 \Rightarrow 3a \leq 0 \Rightarrow a \leq 0$$
因此 $$a$$ 的取值范围为 $$[-\frac{5}{2}, 0]$$,选项 C 正确。
第4题解析:
虚数 $$(x - 2) + yi$$ 的模为 $$1$$,即 $$(x - 2)^2 + y^2 = 1$$。设 $$t = \frac{y}{x}$$,则 $$y = tx$$。代入方程:
$$(x - 2)^2 + (tx)^2 = 1 \Rightarrow x^2 - 4x + 4 + t^2x^2 = 1 \Rightarrow (1 + t^2)x^2 - 4x + 3 = 0$$
判别式 $$\Delta \geq 0$$:$$16 - 12(1 + t^2) \geq 0 \Rightarrow t^2 \leq \frac{1}{3}$$
因此 $$t \in [-\frac{\sqrt{3}}{3}, \frac{\sqrt{3}}{3}]$$,且 $$x \neq 0$$(否则模不为 $$1$$),所以 $$t \neq 0$$。选项 B 正确。
第5题解析:
直线 $$AB$$ 的斜率 $$k = \frac{3\sqrt{3} - \sqrt{3}}{-1 - 1} = \frac{2\sqrt{3}}{-2} = -\sqrt{3}$$
倾斜角 $$\theta$$ 满足 $$\tan \theta = -\sqrt{3}$$,因此 $$\theta = 120^\circ$$,选项 C 正确。
第6题解析:
直线 $$l: mx + y - m - 1 = 0$$ 与线段 $$MN$$(端点 $$M(2, -1)$$ 和 $$N(-4, -2)$$)相交。计算直线在 $$M$$ 和 $$N$$ 处的值:
在 $$M$$ 点:$$2m - 1 - m - 1 \leq 0 \Rightarrow m - 2 \leq 0 \Rightarrow m \leq 2$$
在 $$N$$ 点:$$-4m - 2 - m - 1 \geq 0 \Rightarrow -5m - 3 \geq 0 \Rightarrow m \leq -\frac{3}{5}$$
因此 $$m \in (-\infty, -\frac{3}{5}] \cup [2, +\infty)$$,选项 D 正确。
第7题解析:
直线 $$AB$$ 与 $$2x - y + 1 = 0$$ 平行,因此斜率相同:
$$\frac{8 - a}{a - (-1)} = 2 \Rightarrow 8 - a = 2a + 2 \Rightarrow 6 = 3a \Rightarrow a = 2$$
答案为 B。
第8题解析:
抛物线 $$y = 2x^2$$ 上两点 $$A(x_1, y_1)$$ 和 $$B(x_2, y_2)$$ 关于直线 $$y = x + m$$ 对称,因此中点在直线上且斜率乘积为 $$-1$$:
中点坐标 $$\left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)$$ 满足 $$y = x + m$$,且斜率 $$\frac{y_2 - y_1}{x_2 - x_1} = -1$$。
由 $$x_1x_2 = -\frac{3}{4}$$ 和抛物线方程,解得 $$m = 2$$,选项 A 正确。
第9题解析:
函数 $$f(x) = ax^2 + (a - 1)\ln x + 1$$,两点 $$A$$ 和 $$B$$ 的斜率绝对值不小于 $$2$$。求导后分析极值点,得到 $$a \leq -\frac{1}{2}$$,选项 D 正确。
第10题解析:
椭圆 $$C: \frac{x^2}{4} + y^2 = 1$$,直线 $$l$$ 与椭圆交于 $$A$$ 和 $$B$$,中点为 $$(-1, \frac{1}{2})$$。利用点差法:
$$\frac{x_1 + x_2}{2} = -1$$,$$\frac{y_1 + y_2}{2} = \frac{1}{2}$$,代入椭圆方程得斜率 $$k = \frac{1}{2}$$。
直线方程为 $$y - \frac{1}{2} = \frac{1}{2}(x + 1)$$,化简为 $$x - 2y + 2 = 0$$,选项 B 正确。
.jpg)