正确率60.0%曲线$$y=2 x-e^{x}$$在$${{x}{=}{0}}$$处的切线的倾斜角为()
B
A.$${{0}}$$
B.$$\frac{\pi} {4}$$
C.$$\frac{\pi} {2}$$
D.$$\frac{3 \pi} {4}$$
2、['直线的方向向量与斜率的关系', '向量垂直', '直线的倾斜角']正确率60.0%关于直线$$l,$$,下列说法正确的是()
B
A.直线$${{l}}$$的倾斜角为$${{6}{0}{^{∘}}}$$
B.向量$$\vec{v}=( \sqrt{3}, 1 )$$是直线$${{l}}$$的一个方向向量
C.直线$${{l}}$$经过点$$( 1,-\sqrt{3} )$$
D.向量$$\vec{n}=( 1, \sqrt{3} )$$是直线$${{l}}$$的一个法向量
3、['空间中直线的方向向量与直线的向量表示', '直线的倾斜角']正确率80.0%直线$${{l}}$$的一方向向量为$$( 2, 3 )$$,则它的斜率$${{k}}$$为$${{(}{)}}$$
A
A.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
B.$$\frac{1} {2}$$
C.$$- \frac{1} {2}$$
D.$$- \frac{3} {2}$$
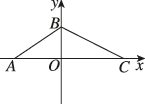
4、['直线的斜率', '直线的倾斜角']正确率60.0%如图的顶点都在坐标轴上,直线$${{A}{B}}$$的斜率为$$\frac{2} {3},$$直线$${{B}{C}}$$的斜率为$$- \frac1 2,$$则$$\operatorname{t a n} \angle A B C=$$()
C
A.$$- \frac{1} {4}$$
B.$$- \frac{7} {8}$$
C.$$- \frac{7} {4}$$
D.$$- \frac{7} {2}$$
5、['直线的斜率', '直线的倾斜角']正确率80.0%已知直线$${{l}}$$:$$x+y-2=0,$$则直线$${{l}}$$的倾斜角为()
D
A.$$\frac{\pi} {4}$$
B.$$\frac{\pi} {2}$$
C.$$\frac{2 \pi} {3}$$
D.$$\frac{3 \pi} {4}$$
6、['直线的斜率', '直线的倾斜角']正确率60.0%在平面直角坐标系$${{x}{O}{y}}$$中,直线$$l \colon~ x-y=0$$的倾斜角为$${{(}{)}}$$
B
A.$${{0}^{∘}}$$
B.$${{4}{5}^{∘}}$$
C.$${{9}{0}^{∘}}$$
D.$${{1}{3}{5}^{∘}}$$
7、['两点间的斜率公式', '简单复合函数的导数', '导数的四则运算法则', '导数的几何意义', '直线的斜率', '直线的倾斜角']正确率60.0%已知曲线$$y=-\frac{1} {2} x^{2}-2$$上一点$$P ( 1,-\frac{5} {2} )$$,则在点$${{P}}$$处的切线的倾斜角为()
C
A.$${{3}{0}^{∘}}$$
B.$${{4}{5}^{∘}}$$
C.$${{1}{3}{5}^{∘}}$$
D.$${{1}{6}{5}^{∘}}$$
8、['两点间的斜率公式', '直线的斜率', '直线的倾斜角']正确率60.0%过两点$$(-1, 0 ), ~ ( 2, \sqrt{3} )$$的直线斜率为()
A
A.$$\frac{\sqrt{3}} {3}$$
B.$$- \frac{\sqrt3} {3}$$
C.$${{−}{\sqrt {3}}}$$
D.$${\sqrt {3}}$$
9、['直线的斜率', '直线的倾斜角']正确率60.0%已知直线$${{l}}$$的斜率的绝对值等于$${\sqrt {3}{,}}$$则直线的倾斜角为()
C
A.$${{6}{0}^{∘}}$$
B.$${{3}{0}^{∘}}$$
C.$${{6}{0}^{∘}}$$或$${{1}{2}{0}^{∘}}$$
D.$${{3}{0}^{∘}}$$或$${{1}{5}{0}^{∘}}$$
10、['直线的倾斜角']正确率40.0%已知点$$A ( 2,-3 )$$,$$B (-3,-2 )$$,直线$${{m}}$$过$$P ( 1, 1 )$$,且与线段$${{A}{B}}$$相交,求直线$${{m}}$$的斜率$${{k}}$$的取值范围为$${{(}{)}}$$
A
A.$$k \geq\frac3 4 \div k \leq-4$$
B.$$k \geq\frac3 4 \ddag k \leq-\frac1 4$$
C.$$- 4 \leqslant k \leqslant\frac{3} {4}$$
D.$$\frac{3} {4} \leqslant k \leqslant4$$
1. 首先求曲线 $$y = 2x - e^x$$ 在 $$x = 0$$ 处的导数:
$$y' = \frac{d}{dx}(2x - e^x) = 2 - e^x$$
在 $$x = 0$$ 处,导数为 $$y'(0) = 2 - e^0 = 1$$。
切线的斜率 $$k = 1$$,对应的倾斜角为 $$\arctan(1) = \frac{\pi}{4}$$。
正确答案是 B。
2. 选项分析:
A. 题目未给出直线 $$l$$ 的具体方程,无法直接确定倾斜角。
B. 向量 $$\vec{v} = (\sqrt{3}, 1)$$ 是直线 $$l$$ 的方向向量,说明斜率 $$k = \frac{1}{\sqrt{3}}$$,符合方向向量的定义。
C. 题目未给出直线经过的点,无法确认。
D. 向量 $$\vec{n} = (1, \sqrt{3})$$ 是直线 $$l$$ 的法向量,说明斜率 $$k = -\frac{1}{\sqrt{3}}$$,与选项 B 矛盾。
因此,只有选项 B 是正确的。
正确答案是 B。
3. 方向向量为 $$(2, 3)$$,斜率 $$k = \frac{3}{2}$$。
正确答案是 A。
4. 设 $$\angle ABC$$ 的两边斜率分别为 $$k_{AB} = \frac{2}{3}$$ 和 $$k_{BC} = -\frac{1}{2}$$。
倾斜角的正切值为:
$$\tan \angle ABC = \left| \frac{k_{BC} - k_{AB}}{1 + k_{AB} \cdot k_{BC}} \right| = \left| \frac{-\frac{1}{2} - \frac{2}{3}}{1 + \frac{2}{3} \cdot (-\frac{1}{2})} \right| = \left| \frac{-\frac{7}{6}}{\frac{2}{3}} \right| = \frac{7}{4}$$。
由于 $$\angle ABC$$ 为钝角,取负值。
正确答案是 C。
5. 直线 $$l: x + y - 2 = 0$$ 的斜率为 $$k = -1$$。
倾斜角为 $$\arctan(-1) = \frac{3\pi}{4}$$。
正确答案是 D。
6. 直线 $$l: x - y = 0$$ 的斜率为 $$k = 1$$。
倾斜角为 $$\arctan(1) = 45^\circ$$。
正确答案是 B。
7. 曲线 $$y = -\frac{1}{2}x^2 - 2$$ 的导数为 $$y' = -x$$。
在点 $$P(1, -\frac{5}{2})$$ 处的斜率为 $$y'(1) = -1$$。
倾斜角为 $$\arctan(-1) = 135^\circ$$。
正确答案是 C。
8. 过两点 $$(-1, 0)$$ 和 $$(2, \sqrt{3})$$ 的斜率为:
$$k = \frac{\sqrt{3} - 0}{2 - (-1)} = \frac{\sqrt{3}}{3}$$。
正确答案是 A。
9. 直线斜率的绝对值为 $$\sqrt{3}$$,因此斜率 $$k = \sqrt{3}$$ 或 $$k = -\sqrt{3}$$。
对应的倾斜角为 $$60^\circ$$ 或 $$120^\circ$$。
正确答案是 C。
10. 直线 $$m$$ 过点 $$P(1, 1)$$,与线段 $$AB$$ 相交,其中 $$A(2, -3)$$ 和 $$B(-3, -2)$$。
计算斜率范围:
$$k_{PA} = \frac{-3 - 1}{2 - 1} = -4$$,
$$k_{PB} = \frac{-2 - 1}{-3 - 1} = \frac{3}{4}$$。
因此,斜率 $$k$$ 的取值范围为 $$k \leq -4$$ 或 $$k \geq \frac{3}{4}$$。
正确答案是 A。
.jpg)