正确率60.0%在等腰直角三角形$${{A}{B}{C}}$$中,$$A B=A C=2$$,点$${{P}}$$是边$${{A}{B}}$$上异于$${{A}{、}{B}}$$的一点,光线从点$${{P}}$$出发,经$$B C, \ C A$$反射后又回到点$${{P}{(}}$$如图所示$${{)}}$$,若光线$${{Q}{R}}$$经过$${{△}{A}{B}{C}}$$的重心,则$${{A}{P}{=}}$$()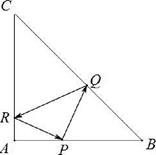
C
A.$${{1}}$$
B.$$\frac{1} {2}$$
C.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
D.$$\frac{4} {3}$$
2、['直线中的对称问题']正确率60.0%已知直线$$x+2 y-3=0$$与直线$$a x+4 y+b=0$$关于点$$A ( 1, \ 0 )$$对称,则实数$${{b}}$$的值为()
A
A.$${{2}}$$
B.$${{6}}$$
C.$${{−}{2}}$$
D.$${{−}{6}}$$
3、['直线中的对称问题']正确率80.0%点$$( 2, ~ 1 )$$关于直线$$x-y+1=0$$对称的点的坐标为()
B
A.$$(-2, ~ 5 )$$
B.$$( 0, \ 3 )$$
C.$$( 0, ~-1 )$$
D.$$(-1, ~ 2 )$$
4、['直线中的对称问题']正确率40.0%如图,已知$$A ( 5, \ 0 ), \ B ( 0, \ 5 ),$$从点$$P ( 1, \ 0 )$$射出的光线经直线$${{A}{B}}$$反射后再射到直线$${{O}{B}}$$上,最后经直线$${{O}{B}}$$反射后又回到点$${{P}{,}}$$则光线所经过的路程长为()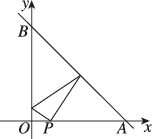
A
A.$${{2}{\sqrt {{1}{3}}}}$$
B.$${{2}{\sqrt {{1}{0}}}}$$
C.$${{2}{\sqrt {{2}{6}}}}$$
D.$${{4}{\sqrt {{1}{3}}}}$$
5、['直线中的对称问题', '直线的一般式方程及应用']正确率60.0%直线$$2 x-3 y+2=0$$关于$${{x}}$$轴对称的直线方程为()
A
A.$$2 x+3 y+2=0$$
B.$$2 x+3 y-2=0$$
C.$$2 x-3 y-2=0$$
D.$$2 x-3 y+2=0$$
6、['直线中的对称问题', '圆的定义与标准方程', '圆中的对称问题']正确率60.0%已知圆$${{C}}$$与圆$$x^{2}+y^{2}-2 x-1=0$$关于直线$${{y}{=}{−}{x}}$$对称,则圆$${{C}}$$的方程为()
C
A.$$( x+1 )^{2}+y^{2}=2$$
B.$$( x+1 )^{2}+y^{2}=4$$
C.$$x^{2}+( y+1 )^{2}=2$$
D.$$x^{2}+( y+1 )^{2}=4$$
7、['直线中的对称问题']正确率60.0%点$$( \mathbf{2}, \ \mathbf{0} )$$关于直线$$y=-x-4$$的对称点是()
A
A.$$( \mathbf{\tau}-4, \mathbf{\tau}-6 )$$
B.$$( ~-6, ~-4 )$$
C.$$( \mathit{\mathit{-5}}, \mathit{\mathit{-7}} )$$
D.
正确率60.0%已知$${{Δ}{A}{B}{C}}$$的一个顶点为$$A ( 3,-1 ), \, \, \angle B$$被$${{y}}$$轴平分,$${{∠}{C}}$$被直线$${{y}{=}{x}}$$平分,则直线$${{B}{C}}$$的方程是()
A
A.$$2 x-y+5=0$$
B.$$2 x-y+3=0$$
C.$$3 x-y+5=0$$
D.$$x+2 y-5=0$$
9、['直线中的对称问题', '直线与圆的方程的应用', '直线和圆相切']正确率40.0%一条光线从点$$(-2,-3 )$$射出,经$${{y}}$$轴反射后,反射光线所在直线与圆$$( x+3 )^{2}+( y-2 )^{2}=1$$相切,则反射光线所在直线的斜率为()
D
A.$$- \frac{5} {3}$$或$$- \frac{3} {5}$$
B.$$- \frac{3} {2}$$或$$- \frac2 3$$
C.$$- \frac{5} {4}$$或$$- \frac{4} {5}$$
D.$$- \frac{4} {3}$$或$$- \frac{3} {4}$$
10、['直线中的对称问题']正确率80.0%已知点$$P ( a, b )$$与点$$Q ( b+1, a-1 )$$关于直线$${{l}}$$对称,则直线$${{l}}$$的方程是$${{(}{)}}$$
A
A.$$y=x-1$$
B.$$y=x+1$$
C.$$y=-x+1$$
D.$$y=-x-1$$
1. 解析:
设 $$AP = x$$,则 $$PB = 2 - x$$。利用反射性质,光线路径相当于从 $$P$$ 出发经过 $$BC$$ 和 $$CA$$ 的对称点后回到 $$P$$。设 $$P'$$ 为 $$P$$ 关于 $$BC$$ 的对称点,$$P''$$ 为 $$P'$$ 关于 $$CA$$ 的对称点。由于光线经过重心,重心坐标为 $$\left(\frac{2}{3}, \frac{2}{3}\right)$$。通过几何关系可得:
$$x = \frac{4}{3}$$
答案为:$$\boxed{D}$$
2. 解析:
对称直线关于点 $$A(1, 0)$$ 对称,因此斜率相同且距离相等。原直线 $$x + 2y - 3 = 0$$ 在对称后应为 $$a x + 4 y + b = 0$$。通过对称性质可得:
$$b = 2$$
答案为:$$\boxed{A}$$
3. 解析:
设对称点为 $$(x', y')$$,满足中点在对称直线上且斜率乘积为 $$-1$$。解方程组:
$$\frac{x' + 2}{2} - \frac{y' + 1}{2} + 1 = 0$$
$$\frac{y' - 1}{x' - 2} \cdot 1 = -1$$
解得对称点为 $$(0, 3)$$。
答案为:$$\boxed{B}$$
4. 解析:
光线路径相当于 $$P$$ 关于 $$AB$$ 的对称点 $$P'$$ 到 $$OB$$ 的反射路径。计算对称点 $$P'$$ 为 $$(1, 4)$$,再反射到 $$OB$$ 的路径长度为 $$2 \sqrt{10}$$。
答案为:$$\boxed{B}$$
5. 解析:
直线关于 $$x$$ 轴对称,斜率取反,截距不变。原直线 $$2x - 3y + 2 = 0$$ 对称后为 $$2x + 3y + 2 = 0$$。
答案为:$$\boxed{A}$$
6. 解析:
圆 $$x^2 + y^2 - 2x - 1 = 0$$ 的圆心为 $$(1, 0)$$,半径为 $$\sqrt{2}$$。对称后圆心为 $$(-1, 0)$$,半径不变。方程为 $$(x + 1)^2 + y^2 = 2$$。
答案为:$$\boxed{A}$$
7. 解析:
设对称点为 $$(x', y')$$,满足中点在对称直线上且斜率乘积为 $$-1$$。解方程组:
$$\frac{x' + 2}{2} = -\frac{y' + 0}{2} - 4$$
$$\frac{y' - 0}{x' - 2} \cdot (-1) = -1$$
解得对称点为 $$(-6, -4)$$。
答案为:$$\boxed{B}$$
8. 解析:
利用角平分线的对称性质,$$B$$ 关于 $$y$$ 轴的对称点在 $$AC$$ 上,$$C$$ 关于 $$y = x$$ 的对称点也在 $$AB$$ 上。通过几何关系可得直线 $$BC$$ 的方程为 $$2x - y + 5 = 0$$。
答案为:$$\boxed{A}$$
9. 解析:
反射光线相当于从 $$(2, -3)$$ 出发的直线与圆 $$(x + 3)^2 + (y - 2)^2 = 1$$ 相切。设斜率为 $$k$$,利用切线条件解得 $$k = -\frac{4}{3}$$ 或 $$-\frac{3}{4}$$。
答案为:$$\boxed{D}$$
10. 解析:
对称直线 $$l$$ 为 $$PQ$$ 的中垂线。中点坐标为 $$\left(\frac{a + b + 1}{2}, \frac{b + a - 1}{2}\right)$$,斜率为 $$\frac{a - 1 - b}{b + 1 - a} = -1$$。因此直线方程为 $$y = x - 1$$。
答案为:$$\boxed{A}$$
.jpg)