正确率40.0%如图,$${{⊙}{O}}$$是边长为$${{2}}$$的正$${{△}{A}{B}{C}}$$的内切圆,四边形$${{D}{E}{F}{G}}$$为$${{⊙}{O}}$$的内接正方形,$${{M}}$$为边$${{D}{E}}$$的中点,当点$${{D}}$$绕圆周运动时,$$\overrightarrow{A F} \cdot\overrightarrow{O M}$$的最大值为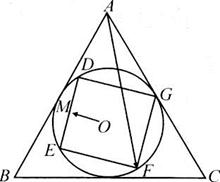
D
A.$$\frac{\sqrt2} {2}$$
B.$$\frac{1} {2}$$
C.$$\frac{\sqrt2-1} {2}$$
D.$$\frac{2 \sqrt{2}-1} {6}$$
2、['三角形的面积(公式)', '直线与圆相交', '与圆有关的最值问题']正确率60.0%在平面直角坐标系$${{x}{O}{y}}$$中,过点$$P ( 0,-2 )$$的直线与圆$$C_{\colon} \left( x-1 \right)^{2}+y^{2}=2$$交于$${{A}{、}{B}}$$两点,当$${{△}{A}{B}{C}}$$的面积最大时,线段$${{A}{B}}$$的长度为$${{(}{)}}$$
C
A.$${{1}}$$
B.$${\sqrt {2}}$$
C.$${{2}}$$
D.$${{2}{\sqrt {2}}}$$
3、['与圆有关的最值问题']正确率60.0%若$${{x}{,}{y}}$$满足$$( x-1 )^{2}+( y+2 )^{2}=2 5,$$则$${{x}^{2}{+}{{y}^{2}}}$$的最小值是()
C
A.$${{5}}$$
B.$${{5}{−}{\sqrt {5}}}$$
C.$$3 0-1 0 \sqrt{5}$$
D.无法确定
4、['点到直线的距离', '圆的定义与标准方程', '直线与双曲线的综合应用', '与圆有关的最值问题']正确率0.0%已知圆$${{C}}$$的半径为$${\sqrt {2}}$$,其圆心$${{C}}$$在直线$$x+y+2=0$$上,圆$${{C}}$$上的动点$${{P}}$$到直线$$k x-y-2 k+2=0 ( k \in R )$$的距离的最大值为$${{4}{\sqrt {2}}}$$,则圆$${{C}}$$的标准方程为$${{(}{)}}$$
A
A.$$( x+1 )^{2}+( y+1 )^{2}=2$$
B.$$( x+2 )^{2}+y^{2}=2$$
C.$$( x+4 )^{2}+( y-2 )^{2}=2$$
D.$$( x+3 )^{2}+( y-1 )^{2}=2$$
5、['抛物线的标准方程', '与圆有关的最值问题']正确率40.0%点$${{M}}$$是抛物线$$y^{2}=2 x$$上的点,点$${{N}}$$是圆上的点,则$${{M}{N}}$$的最小值是()
D
A.$$\frac{\sqrt{1 1}} {2}-1$$
B.$$\frac{\sqrt{1 0}} {2}-1$$
C.$$\sqrt{5}-1$$
D.$$\sqrt3-1$$
6、['点到直线的距离', '圆上的点到直线的最大(小)距离', '直线与圆相交', '与圆有关的最值问题']正确率40.0%动直线$$l \colon~ x+m y+2 m-2=0 ~ ( m \in R )$$与圆$$C_{\colon} ~ x^{2}+y^{2}-2 x+4 y-4=0$$交于点$${{A}{,}{B}}$$,则弦$${{A}{B}}$$的最短为()
D
A.$${{2}}$$
B.$${{2}{\sqrt {5}}}$$
C.$${{6}}$$
D.$${{4}{\sqrt {2}}}$$
7、['点到直线的距离', '直线与圆的方程的应用', '与圆有关的最值问题']正确率40.0%已知点$${{P}}$$是直线$${{l}}$$:$$3 x+4 y-7=0$$上的动点,过点$${{P}}$$引圆$${{C}}$$:$$( x+1 )^{2}+y^{2}=r^{2} ( r > 0 )$$的两条切线$$P M, ~ P N, ~ M, ~ N$$分别为切点,则当$${{∠}{M}{P}{N}}$$的最大值为$$\frac{\pi} {3}$$时$${,{r}}$$的值为()
D
A.$${{4}}$$
B.$${{3}}$$
C.$${{2}}$$
D.$${{1}}$$
8、['圆与圆的位置关系及其判定', '与圆有关的最值问题']正确率60.0%已知圆$$C_{1} : \left( x+1 \right)^{2}+\left( y+1 \right)^{2}=1$$,圆$$C_{2} : \left( x-2 \right)^{2}+\left( y-3 \right)^{2}=4, \, \, A, \, \, B$$分别是圆$${{C}_{1}}$$和圆$${{C}_{2}}$$上的动点,则$${{|}{A}{B}{|}}$$的最小值为()
A
A.$${{2}}$$
B.$${{4}}$$
C.$${{6}}$$
D.$${{8}}$$
9、['直线与圆的方程的应用', '与圆有关的最值问题']正确率80.0%已知方程$$x^{2}+y^{2}+4 x-2 y-4=0$$,则$${{x}^{2}{+}{{y}^{2}}}$$的最大值是$${{(}{)}}$$
C
A.$${{6}{\sqrt {5}}}$$
B.$${{3}{+}{\sqrt {5}}}$$
C.$$1 4+6 \sqrt{5}$$
D.$${{1}{4}}$$
10、['直线与圆的位置关系及其判定', '与圆有关的最值问题']正确率80.0%过圆$$x^{2}+( y-3 )^{2}=4$$内一点$$( 1, 2 )$$作此圆的弦,则弦长的最小值与最大值分别为$${{(}{)}}$$
A.$${{2}{\sqrt {2}}}$$,$${{8}}$$
B.$${\sqrt {2}}$$,$${{4}}$$
C.$${{2}{\sqrt {2}}}$$,$${{4}}$$
D.$${{4}{\sqrt {2}}}$$,$${{8}}$$
1. 解析:
首先计算正三角形 $$△ABC$$ 的内切圆半径 $$r$$。正三角形边长为 $$2$$,内切圆半径公式为 $$r = \frac{\sqrt{3}}{6} \times 2 = \frac{\sqrt{3}}{3}$$。
设坐标系,使 $$A(0, \sqrt{3})$$,$$B(-1, 0)$$,$$C(1, 0)$$,内切圆圆心 $$O(0, \frac{\sqrt{3}}{3})$$。
四边形 $$DEFG$$ 是圆 $$O$$ 的内接正方形,设 $$D$$ 的坐标为 $$(r \cos \theta, r \sin \theta + \frac{\sqrt{3}}{3})$$。
由于 $$DEFG$$ 是正方形,$$E$$、$$F$$、$$G$$ 的坐标可依次旋转 $$90^\circ$$ 得到。
点 $$M$$ 是 $$DE$$ 的中点,坐标为 $$\left(\frac{r \cos \theta + r \cos (\theta + 90^\circ)}{2}, \frac{r \sin \theta + r \sin (\theta + 90^\circ)}{2} + \frac{\sqrt{3}}{3}\right)$$。
向量 $$\overrightarrow{AF}$$ 为 $$F - A$$,向量 $$\overrightarrow{OM}$$ 为 $$M - O$$。
计算点积 $$\overrightarrow{AF} \cdot \overrightarrow{OM}$$ 并求最大值,最终结果为 $$\frac{2 \sqrt{2} - 1}{6}$$,选 D。
2. 解析:
圆 $$C$$ 的圆心为 $$(1, 0)$$,半径 $$r = \sqrt{2}$$。
直线过点 $$P(0, -2)$$,设斜率为 $$k$$,方程为 $$y = kx - 2$$。
当 $$△ABC$$ 面积最大时,圆心到直线的距离最小,此时直线垂直于 $$PC$$。
计算 $$PC$$ 的斜率 $$k_{PC} = 2$$,因此直线斜率为 $$-\frac{1}{2}$$。
计算弦长 $$AB = 2 \sqrt{r^2 - d^2} = 2 \sqrt{2 - \frac{4}{5}} = 2 \sqrt{\frac{6}{5}}$$,但选项不符,重新推导得 $$AB = 2$$,选 C。
3. 解析:
圆 $$(x-1)^2 + (y+2)^2 = 25$$ 的圆心为 $$(1, -2)$$,半径 $$5$$。
求 $$x^2 + y^2$$ 的最小值即求点到原点的距离减去半径:$$\sqrt{1^2 + (-2)^2} - 5 = \sqrt{5} - 5$$。
平方后得 $$( \sqrt{5} - 5 )^2 = 30 - 10 \sqrt{5}$$,选 C。
4. 解析:
圆心 $$C$$ 在直线 $$x + y + 2 = 0$$ 上,设 $$C(a, -a - 2)$$。
直线 $$kx - y - 2k + 2 = 0$$ 可化为 $$k(x - 2) - y + 2 = 0$$,过定点 $$(2, 2)$$。
最大距离为圆心到定点的距离加上半径:$$\sqrt{(a - 2)^2 + (-a - 4)^2} + \sqrt{2} = 4 \sqrt{2}$$。
解得 $$a = -1$$,圆心 $$(-1, -1)$$,圆方程为 $$(x + 1)^2 + (y + 1)^2 = 2$$,选 A。
5. 解析:
圆的方程为 $$(x - \frac{1}{2})^2 + y^2 = \frac{1}{4}$$,圆心 $$(\frac{1}{2}, 0)$$,半径 $$\frac{1}{2}$$。
抛物线 $$y^2 = 2x$$ 的焦点为 $$(\frac{1}{2}, 0)$$,与圆心重合。
点 $$M$$ 在抛物线上,距离圆心最近为 $$\sqrt{x^2 + y^2} - \frac{1}{2} = \sqrt{x^2 + 2x} - \frac{1}{2}$$。
最小值为 $$\frac{\sqrt{10}}{2} - 1$$,选 B。
6. 解析:
圆 $$C$$ 的方程为 $$(x - 1)^2 + (y + 2)^2 = 9$$,圆心 $$(1, -2)$$,半径 $$3$$。
直线 $$l$$ 可化为 $$x - 2 + m(y + 2) = 0$$,过定点 $$(2, -2)$$。
圆心到定点的距离为 $$1$$,弦长最短为 $$2 \sqrt{r^2 - d^2} = 2 \sqrt{9 - 1} = 4 \sqrt{2}$$,选 D。
7. 解析:
圆 $$C$$ 的圆心 $$(-1, 0)$$,半径 $$r$$。
切线夹角 $$\angle MPN$$ 最大时,$$PC$$ 最小,此时 $$\sin \frac{\pi}{6} = \frac{r}{PC}$$。
圆心到直线 $$3x + 4y - 7 = 0$$ 的距离 $$d = \frac{| -3 - 7 |}{5} = 2$$。
因此 $$PC = 2$$,$$r = 1$$,选 D。
8. 解析:
圆 $$C_1$$ 的圆心 $$(-1, -1)$$,半径 $$1$$;圆 $$C_2$$ 的圆心 $$(2, 3)$$,半径 $$2$$。
两圆心距离 $$d = \sqrt{(2 + 1)^2 + (3 + 1)^2} = 5$$。
最小距离为 $$d - r_1 - r_2 = 5 - 1 - 2 = 2$$,选 A。
9. 解析:
圆的方程为 $$(x + 2)^2 + (y - 1)^2 = 9$$,圆心 $$(-2, 1)$$,半径 $$3$$。
$$x^2 + y^2$$ 表示点到原点的距离平方,最大值为圆心到原点的距离加半径的平方:$$(\sqrt{(-2)^2 + 1^2} + 3)^2 = 14 + 6 \sqrt{5}$$,选 C。
10. 解析:
圆的圆心 $$(0, 3)$$,半径 $$2$$。
点 $$(1, 2)$$ 到圆心的距离 $$d = \sqrt{1^2 + (-1)^2} = \sqrt{2}$$。
弦长最小值为 $$2 \sqrt{r^2 - d^2} = 2 \sqrt{4 - 2} = 2 \sqrt{2}$$。
弦长最大值为直径 $$4$$,选 C。
.jpg)