.jpg)
正确率80.0%
电磁炮是利用电磁发射技术制成的新型武器，如图所示为电磁炮的原理结构示意图。若某水平发射轨道长$${{7}{.}{5}{m}}$$，宽$${{1}{.}{5}{m}}$$，发射的炮弹质量为$${{5}{0}{g}}$$，炮弹被发射时从轨道左端由静止开始加速。当电路中的电流恒为$${{2}{0}{A}}$$时，炮弹被发射后的最大速度可达$$3 \times1 0^{3} m / s$$，轨道间磁场为匀强磁场，不计空气及摩擦阻力。下列说法正确的是$${{(}{)}}$$
A.磁场方向为竖直向下
B.磁场方向为水平向右
C.磁场的磁感应强度大小为$${{1}{×}{{1}{0}^{3}}{T}}$$
D.炮弹的加速度大小为$$3 \times1 0^{5} \， m / s^{2}$$
2、['磁场对通电导线的作用力'， '闭合电路的欧姆定律'， '胡克定律']正确率40.0%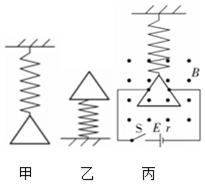
有一劲度系数为$${{k}}$$的轻质绝缘弹簧，将边长为$${{d}}$$的正三角形匀质金属线框$${{(}}$$线框由电阻为$${{R}}$$的金属丝折合而成$${{)}}$$如图甲、乙情况放置，静止时弹簧的长度分别为$${{L}_{1}}$$和$${{L}_{2}}$$。现将该金属线框如图丙所示接入电路，导线的左右接触点分别为线框左右两边的中点，磁场方向垂直纸面向外，大小为$${{B}}$$，电源的电动势为$${{E}}$$，内电阻为$${{r}}$$，导线与线框之间作用力可以忽略，则闭合开关$${{S}}$$后，弹簧的长度$${{L}_{3}}$$为$${{(}{)}}$$
A
A.$$L_{1}+\frac{9 B d E} {2 k ( 2 R+9 r )}$$
B.$$L_{2}+\frac{9 B d E} {2 k ( 2 R+9 r )}$$
C.$$L_{1}-\frac{5 B d E} {2 k ( 2 R+9 r )}$$
D.$$L_{2}+\frac{5 B d E} {2 k ( 2 R+9 r )}$$
3、['安培力的大小简单计算及应用'， '磁场对通电导线的作用力']正确率80.0%一根长为$${{0}{.}{2}{m}}$$、通有$${{2}{A}}$$电流的通电导线放在磁感应强度为$${{0}{.}{5}{T}}$$的匀强磁场中，则其受到的安培力的大小可能是$${{(}{)}}$$
D
A.$${{0}{.}{5}{N}}$$
B.$${{0}{.}{4}{N}}$$
C.$${{0}{.}{3}{N}}$$
D.$${{0}{.}{1}{N}}$$
4、['磁场对通电导线的作用力'， '平行通电直导线之间的相互作用']正确率80.0%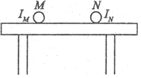
如图所示，在光滑绝缘的水平桌面上，有垂直桌面竖直方向的匀强磁场$${{(}}$$图中未画出$${{)}}$$。现有两条平行通电金属直导线$${{M}}$$和$${{N}}$$，恰好平行且静止在桌面上，图中为垂直导线的截面图，$${{M}}$$和$${{N}}$$中电流大小分别为$${{I}_{M}}$$、$${{I}_{N}}$$，则下列判断正确的是$${{(}{)}}$$
B
A.$${{I}_{M}{≠}{{I}_{N}}}$$、电流方向相反
B.$${{I}_{M}{=}{{I}_{N}}}$$、电流方向相反
C.$${{I}_{M}{=}{{I}_{N}}}$$、电流方向相同
D.$${{I}_{M}{≠}{{I}_{N}}}$$、电流方向相同
5、['磁场对通电导线的作用力'， '闭合电路的欧姆定律'， '电磁感应中的功能问题'， '法拉第电磁感应定律的表述及表达式'， '导体棒或线圈切割磁感线时引起的感应电动势及计算']正确率80.0%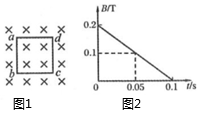
如图所示，垂直于纸面向里的匀强磁场，磁感应强度$${{B}}$$随时间$${{t}}$$均匀变化，磁场方向取垂直纸面向里为正方向。正方形硬质金属框$${{a}{b}{c}{d}}$$放置在磁场中，金属框平面与磁场方向垂直，电阻$${{R}{=}{{0}{.}{1}}{Ω}}$$，边长$${{l}{=}{{0}{.}{2}}{m}}$$。则下列说法错误的是$${{(}{)}}$$
C
A.在$${{t}{=}{0}}$$到$${{t}{=}{{0}{.}{1}}{s}}$$时间内，金属框中的感应电动势为$$0. 0 8 V$$
B.在$${{t}{=}{{0}{.}{0}{5}}{s}}$$时，金属框$${{a}{b}}$$边受到的安培力的大小为$$0. 0 1 6 N$$
C.在$${{t}{=}{{0}{.}{0}{5}}{s}}$$时，金属框$${{a}{b}}$$边受到的安培力的方向垂直于$${{a}{b}}$$向右
D.在$${{t}{=}{0}}$$到$${{t}{=}{{0}{.}{1}}{s}}$$时间内，金属框中电流的电功率为$$0. 0 6 4 W$$
6、['磁场对通电导线的作用力'， '闭合电路的欧姆定律'， '对楞次定律的理解及应用'， '导体棒或线圈切割磁感线时引起的感应电动势及计算']正确率80.0%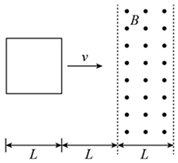
两条平行虚线间存在一匀强磁场，磁感应强度大小$${{B}{=}{{0}{.}{2}}{T}}$$，方向与纸面垂直，边长$${{L}{=}{{0}{.}{1}}{m}}$$、总电阻$${{R}{=}{{0}{.}{0}{5}}{Ω}}$$的正方形导线框$${{a}{b}{c}{d}}$$位于纸面内，$${{c}{d}}$$边距磁场边界$${{L}}$$，如图所示，已知导线框一直向右做匀速直线运动，$${{c}{d}}$$边于$${{t}{=}{1}{s}}$$时刻进入磁场，以初始位置为计时起点，规定：电流沿顺时针方向时的电动势$${{E}}$$为正，磁感线垂直纸面向外时磁通量$${{Φ}}$$为正。则以下关于线框中的感应电动势$${{E}}$$、磁通量$${{Φ}}$$、感应电流$${Ⅰ}$$和安培力$${{F}}$$随时间变化的图象中正确的是$${{(}{)}}$$
B
A.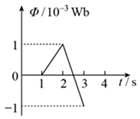
B.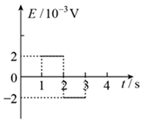
C.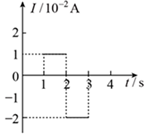
D.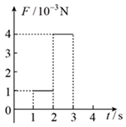
正确率80.0%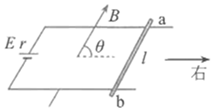
如图所示，水平面内有相距为$${{l}{=}{{0}{.}{4}}{m}}$$的两平行固定金属导轨，导轨左端接有电动势$${{E}{=}{3}{V}}$$、内阻$${{r}{=}{1}{Ω}}$$的电源，金属棒$${{a}{b}}$$跨接在金属导轨上，与两金属导轨垂直并与导轨接触良好，棒$${{a}{b}}$$接入电路部分的电阻$${{R}{=}{1}{Ω}}$$，金属导轨电阻不计。整个装置处于磁感应强度大小$${{B}{=}{1}{T}}$$的匀强磁场中，磁场方向与棒$${{a}{b}}$$垂直且与水平面成$${{θ}{=}{{6}{0}}{°}}$$角斜向右上方，棒$${{a}{b}}$$始终静止于导轨上。下列说法正确的是$${{(}{)}}$$
C
A.棒$${{a}{b}}$$所受摩擦力水平向左
B.通过棒$${{a}{b}}$$的电流为$${{3}{A}}$$
C.棒$${{a}{b}}$$所受安培力大小为$${{0}{.}{6}{N}}$$
D.棒$${{a}{b}}$$所受摩擦力大小为$${{0}{.}{3}{N}}$$
8、['磁场对通电导线的作用力']正确率80.0%欧姆在探索通过导体的电流和电压、电阻关系时，因无电流表，他利用小磁针的偏转来测定电流的大小。其具体做法是：在地磁场作用下小磁针水平静止，在小磁针上方，平行于小磁针水平放置一直导线，当该导线中通有电流时，小磁针会发生偏转。当通过该导线的电流为$${{I}}$$时，小磁针偏转了$${{3}{0}^{∘}}$$若某次实验中，他发现小磁针偏转了$${{6}{0}^{∘}}$$，则通过该直导线的电流为$${{(}}$$已知通电直导线在某点产生的磁场与通过直导线的电流成正比$${{)}{(}}$$$${{)}}$$
A.$${{2}{I}}$$
B.$${{3}{I}}$$
C.$${\sqrt {3}{I}}$$
D.无法确定
9、['磁场对通电导线的作用力'， '闭合电路的欧姆定律'， '导体棒或线圈切割磁感线时引起的感应电动势及计算']正确率80.0%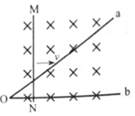
如图所示，导体棒$${{M}{N}}$$和固定导轨$${{O}{a}}$$、$${{O}{b}}$$分别由三种不同材料、粗细均匀的导体制成，匀强磁场垂直于$${{O}{a}}$$、$${{O}{b}}$$所在的水平面，$${{M}{N}}$$搭放在$${{O}{a}}$$、$${{O}{b}}$$上且与$${{O}{b}}$$垂直。在外力作用下，$${{M}{N}}$$沿$${{O}{b}}$$方向匀速运动，运动过程中保持与导轨接触良好。从$${{M}{N}}$$运动到图示位置开始计时，则$${{M}{N}}$$受到的安培力大小$${{F}}$$随时间变化的图像可能正确的是$${{(}{)}}$$
A
A.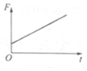
B.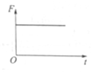
C.
D.
正确率80.0%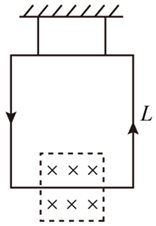
如图所示，质量为$${{m}}$$，边长为$${{L}}$$的金属框通过两根细绳竖直悬挂在房顶上静止，边长为$$\frac{L} {2}$$的正方形区域内有磁感应强度大小为$${{B}}$$。垂直纸面向里的匀强磁场，金属框的下边框处于匀强磁场区域的正中间。当给金属框通入逆时针方向，大小为$${{I}}$$的较小电流时，下列判断正确的是$${{(}{)}}$$
C
A.金属框所受安培力向上，每根绳上的拉力大小$$T=\frac{m g-B I L} {2}$$
B.金属框所受安培力向下，每根绳上的拉力大小$$T=\frac{m g+B I L} {2}$$
C.当电流大小不变，方向反向时，每根绳上的拉力大小$$T^{\prime}=\frac{2 m g+B I L} {4}$$
D.当电流大小不变，方向反向时，每根绳上的拉力大小$$T^{\prime}=\frac{2 m g-B I L} {4}$$
1. 解析：根据电磁炮的工作原理，炮弹在磁场中受到安培力加速。由题目给出的轨道宽度和电流方向，可判断磁场方向应为竖直向下（A正确）。炮弹的最大动能由安培力做功得到：$$F = BIL = ma$$，结合运动学公式$$v^2 = 2aL$$，解得磁感应强度$$B = \frac{mv^2}{2IL^2} = 1 \times 10^3 \, \text{T}$$（C正确）。加速度$$a = \frac{v^2}{2L} = 6 \times 10^5 \, \text{m/s}^2$$（D错误）。综上，正确答案为A、C。
2. 解析：线框接入电路后，电流$$I = \frac{E}{2R + 9r}$$。线框左右两边中点接入电路，有效长度为$$d$$，安培力$$F = BId$$。弹簧受力平衡，伸长量为$$\Delta L = \frac{F}{k} = \frac{BdE}{k(2R + 9r)}$$。由于图丙中安培力方向与图乙相同，故弹簧长度$$L_3 = L_2 + \frac{9BdE}{2k(2R + 9r)}$$（B正确）。
3. 解析：安培力公式$$F = BIL\sin\theta$$，当导线与磁场方向垂直时$$F_{\text{max}} = BIL = 0.2 \, \text{N}$$；当导线与磁场方向平行时$$F = 0$$。因此安培力大小范围为$$0 \leq F \leq 0.2 \, \text{N}$$，选项中只有D（0.1 N）符合。
4. 解析：两导线平行静止，说明安培力相互平衡。根据安培力公式$$F = \frac{\mu_0 I_1 I_2 L}{2\pi d}$$，若电流方向相反，安培力为斥力；若电流方向相同，安培力为引力。题目中两导线静止，故电流方向相反（B、C可能）。由于题目未给出距离$$d$$，无法确定电流大小是否相等，但通常题目隐含$$I_M = I_N$$，故B正确。
5. 解析：金属框中感应电动势$$E = \frac{\Delta B}{\Delta t} \cdot l^2 = 0.08 \, \text{V}$$（A正确）。电流$$I = \frac{E}{R} = 0.8 \, \text{A}$$，安培力$$F = BIl$$，在$$t = 0.05 \, \text{s}$$时$$B = 0.1 \, \text{T}$$，故$$F = 0.016 \, \text{N}$$（B正确）。由楞次定律，安培力方向垂直于$$ab$$向左（C错误）。电功率$$P = I^2 R = 0.064 \, \text{W}$$（D正确）。综上，错误的选项为C。
6. 解析：线框匀速进入磁场，感应电动势$$E = BLv$$，电流$$I = \frac{E}{R}$$。$$cd$$边进入磁场时（$$t = 1 \, \text{s}$$），电动势为正，电流为顺时针方向；完全进入后磁通量不变，电流为零；$$ab$$边离开磁场时（$$t = 2 \, \text{s}$$），电动势为负，电流为逆时针方向。安培力$$F = BIL$$，方向始终阻碍运动。综上，正确的图像为B（电动势随时间变化）和D（安培力随时间变化）。
7. 解析：通过棒的电流$$I = \frac{E}{R + r} = 1.5 \, \text{A}$$（B错误）。安培力$$F = BIl = 0.6 \, \text{N}$$（C正确）。安培力方向垂直磁场与电流方向，分解得水平分量$$F_x = F \sin 60^\circ = 0.3 \, \text{N}$$，摩擦力平衡此分量，方向向左（A、D正确）。综上，错误的选项为B。
8. 解析：地磁场$$B_0$$与电流磁场$$B_I$$的合磁场方向偏转角度$$\theta$$满足$$\tan \theta = \frac{B_I}{B_0}$$。当$$\theta = 30^\circ$$时，$$B_I = B_0 \tan 30^\circ$$；当$$\theta = 60^\circ$$时，$$B_I' = B_0 \tan 60^\circ = 3B_I$$。因$$B_I \propto I$$，故电流为$$3I$$（B正确）。
9. 解析：导体棒匀速运动，感应电动势$$E = BLv$$，电流$$I = \frac{E}{R}$$，安培力$$F = BIL$$。由于导体棒材料不同，电阻率变化可能导致$$R$$随时间变化，故安培力可能非线性变化。图像A（线性增大）和C（非线性变化）可能正确，但题目未给出电阻变化规律，通常默认均匀材料，故A更合理。
10. 解析：金属框通入电流时，下边框受安培力$$F = BI \cdot \frac{L}{2}$$方向向上（A正确）。平衡条件：$$2T + F = mg$$，解得$$T = \frac{mg - BIL}{2}$$（A正确）。电流反向时，安培力向下，平衡条件：$$2T' = mg + F$$，解得$$T' = \frac{2mg + BIL}{4}$$（C正确）。综上，正确答案为A、C。