.jpg)
正确率40.0%如图所示，水平桌面上放置一根条形磁铁，磁铁中央正上方用绝缘弹簧悬挂一水平直导线，并与磁铁垂直。当直导线中通入图中所示方向的电流时，和未通电相比较，可以判断出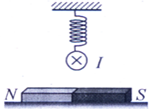
D
A.弹簧的拉力减小，条形磁铁对桌面的压力增大
B.弹簧的拉力减小，条形磁铁对桌面的压力减小
C.弹簧的拉力增大，条形磁铁对桌面的压力增大
D.弹簧的拉力增大，条形磁铁对桌面的压力减小
2、['安培力的大小简单计算及应用'， '利用平衡推论求力']正确率0.0%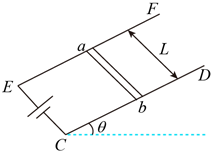
如图所示，两平行金属导轨$${{C}{D}}$$、$${{E}{F}}$$间距为$${{L}}$$，与电动势为$${{E}}$$的电源相连，质量为$${{m}}$$、电阻为$${{R}}$$的金属棒$${{a}{b}}$$垂直于导轨放置构成闭合回路，回路平面与水平面成$${{θ}}$$角，回路其余电阻不计。为使$${{a}{b}}$$棒静止，需在空间施加的匀强磁场磁感强度的最小值及其方向分别为$${{(}{)}}$$
A.$$\frac{m g R} {E L}$$，水平向右
B.$$\frac{m g R \operatorname{t a n} \theta} {E L}$$，竖直向下
C.$$\frac{m g R \operatorname{s i n} \theta} {E L}$$，垂直于回路平面向下
D.$$\frac{m g R \operatorname{c o s} \theta} {E L}$$，垂直于回路平面向上
3、['安培力的大小简单计算及应用'， '安培力作用下的平衡']正确率40.0%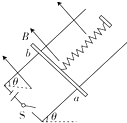
如图所示，两光滑的平行导轨与水平方向成角同定，导轨的下端接有如图所示的电源，一劲度系数为$${{k}}$$
A
A.$$\frac{2 B I L} {k}+x_{0}$$
B.$${\frac{B I L} {k}}+x_{0}$$
C.$$\frac{2 B I L} {k}-x_{0}$$
D.$$\frac{B I L} {k}-x_{0}$$
4、['安培力的大小简单计算及应用'， '磁感应强度的定义、单位及物理意义']正确率60.0%一根长为$${{0}{.}{1}{m}}$$的通电直导线，电流为$${{1}{A}}$$，在匀强磁场中某处受到的磁场力大小为$${{0}{.}{4}{N}}$$，则该处的磁感应强度大小（）
B
A.等于$${{4}{T}}$$
B.大于或等于$${{4}{T}}$$
C.小于或等于$${{4}{T}}$$
D.可能为$${{0}}$$
5、['安培力的大小简单计算及应用'， '安培力作用下的平衡']正确率60.0%如图所示，天平的右臂挂有一水平边长度为$${{L}{、}}$$匝数为$${{N}}$$的矩形线圈，虚线区域内存在垂直线圈所在平面的水平方向的匀强磁场。当线圈中通有逆时针方向$${、}$$大小为$${{I}}$$的电流时，在天平左$${、}$$右两边加上质量分别为$$4 m， \ 3 m$$的砝码，天平恰好平衡。当电流增大为原来的$${{5}}$$倍(方向不变)时，在左边再加上质量为$${{m}}$$的砝码后，天平重新平衡。重力加速度大小为$${{g}}$$。该匀强磁场的磁感应强度$${{(}{)}}$$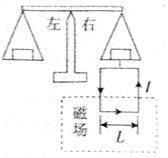
C
A.方向水平向外，大小为$$\frac{m g} {N I L}$$
B.方向水平向里，大小为$$\frac{m g} {2 N I L}$$
C.方向水平向外，大小为$$\frac{m g} {4 N I L}$$
D.方向水平向外，大小为$$\frac{m g} {5 N I L}$$
6、['安培力的大小简单计算及应用'， '电容'， '电容器的充、放电与储能'， '安培力的方向判断（左手定则）']正确率60.0%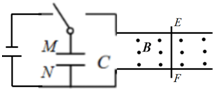
如图所示为航母上电磁弹射装置的等效电路图(俯视图$${{)}}$$
B
A.电源给电容器充电后，$${{M}}$$板带正电
B.导体棒在安培力作用下向右运动
C.超级电容器相当电源，放电时两端电压不变
D.在电容器放电过程中，电容器电容不断减小
7、['安培力的大小简单计算及应用'， '磁感线的定义及特点'， '电场的概念及特征'， '电场线的概念及特点']正确率60.0%有关电场和磁场的下列叙述，正确的是（）
D
A.磁感线越密的地方磁感应强度越大，磁通量也越大
B.沿着电场线的方向，电场强度越来越小
C.安培力的方向一定不与磁场方向垂直
D.回旋加速器中，电场力使带电粒子的速度增大
8、['安培力的大小简单计算及应用'， '安培力作用下的平衡'， '闭合电路欧姆定律内容、表达式、及其能量分析']正确率40.0%如图所示，一光滑绝缘斜面与水平面成$${{4}{5}^{∘}}$$角，匀强磁场的方向竖直向下，磁感应强度大小为$${{B}}$$．把由三段导线$$a b， ~ b c. ~ c a$$构成的一个质量为$${{m}{、}}$$边长为$${{L}}$$的等边三角形线框静置于斜面上，导线$${{a}{c}}$$与斜面底端平行，导线$${{a}{c}}$$的$${{a}{、}{c}}$$端分别接恒定电压的正$${、}$$负两极。若三角形线框静止在斜面上，重力加速度为$${{g}}$$，每段导线的电阻均为$${{R}}$$，则恒定电压$${{U}}$$的大小为（）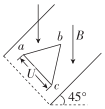
B
A.$$\frac{3 m R} {2 B L}$$
B.$$\frac{2 m g R} {3 B L}$$
C.$$\frac{\sqrt2 B L} {3 m g R}$$
D.$$\frac{2 \sqrt2 B L} {3 m g R}$$
9、['安培力的大小简单计算及应用']正确率60.0%我国西电东送工程中，采用了$$1 1 0 0 K V$$特超高压直流输电技术其中有两个输电塔之间的输电线近似可看成是水平直导线且沿东西方向，两塔之间距离为$${{L}}$$，某时刻输电电流为$${{I}}$$，已知该地区地磁场方向与水平方向的夹角为$${{3}{0}^{∘}}$$，磁感应强度大小为$${{B}}$$．则该时刻其中一根导线所受到地磁场的安培力的大小为（）
C
A.$${\frac{\sqrt{3}} {2}} B I L$$
B.$${\frac{1} {2}} B I L$$
C.$${{B}{I}{L}}$$
D.$${{0}}$$
10、['安培力的大小简单计算及应用'， '直线电流的磁场']正确率80.0%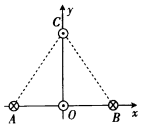
如图所示，$${{A}}$$、$${{B}}$$、$${{C}}$$是等边三角形的三个顶点，$${{O}}$$点是$${{A}}$$、$${{B}}$$两点连线的中点。以$${{O}}$$点为坐标原点，以$${{A}}$$、$${{B}}$$两点的连线为$${{x}}$$轴，以$${{O}}$$、$${{C}}$$两点的连线为$${{y}}$$轴，建立坐标系。过$${{A}}$$、$${{B}}$$、$${{C}}$$、$${{O}}$$四点各有一条长直导线垂直穿过坐标平面，各导线中通有大小相等的电流，其中过$${{A}}$$、$${{B}}$$两点的导线中的电流方向向里，过$${{C}}$$、$${{O}}$$两点的导线中的电流方向向外。过$${{O}}$$点的导线所受安培力的方向为$${{(}{)}}$$
A
A.沿$${{y}}$$轴正方向
B.沿$${{y}}$$轴负方向
C.沿$${{x}}$$轴正方向
D.沿$${{x}}$$轴负方向
1. 解析：
根据安培定则和左手定则，通电导线在磁场中受到安培力作用。图中电流方向向右，磁场方向由条形磁铁的N极指向S极（水平向左），因此安培力方向向上。弹簧的拉力减小，同时条形磁铁对导线的反作用力向下，导致条形磁铁对桌面的压力增大。答案为 A。
2. 解析：
金属棒$$ab$$静止时，需平衡重力分量$$mg\sinθ$$和安培力$$BIL$$。回路电流$$I = \frac{E}{R}$$，因此安培力为$$B \cdot \frac{E}{R} \cdot L$$。最小磁场强度满足$$B \cdot \frac{E}{R} \cdot L = mg\sinθ$$，解得$$B = \frac{mgR\sinθ}{EL}$$，方向垂直于回路平面向下。答案为 C。
3. 解析：
题目不完整，无法解析。
4. 解析：
磁场力公式为$$F = BIL\sinθ$$，当$$θ = 90°$$时，$$B = \frac{F}{IL} = \frac{0.4}{1 \times 0.1} = 4T$$。若$$θ \neq 90°$$，$$B$$需更大才能达到相同力，因此磁感应强度大于或等于$$4T$$。答案为 B。
5. 解析：
天平平衡时，磁场力$$F = NIBL$$。初始平衡方程为$$4mg = 3mg + NIBL$$，解得$$NIBL = mg$$。电流增大为$$5I$$后，新平衡方程为$$4mg + mg = 3mg + 5NIBL$$，解得$$B = \frac{mg}{2NIL}$$，方向水平向里（由左手定则判断）。答案为 B。
6. 解析：
电磁弹射装置中，电源充电后$$M$$板带正电（A正确）；放电时导体棒受安培力向右运动（B正确）；电容器放电时电压逐渐减小（C错误）；电容由结构决定，放电过程中不变（D错误）。答案为 AB。
7. 解析：
磁通量还与面积有关（A错误）；电场强度沿电场线可能不变或变化（B错误）；安培力方向始终垂直于磁场（C错误）；回旋加速器中电场力使粒子加速（D正确）。答案为 D。
8. 解析：
线框静止时，安培力平衡重力分量。等效电路为$$ac$$与$$abc$$并联，总电阻$$R_{总} = \frac{3R}{2}$$。安培力$$F = BIL = B \cdot \frac{U}{R_{总}} \cdot L$$，平衡条件为$$F\cos45° = mg\sin45°$$，解得$$U = \frac{2mgR}{3BL}$$。答案为 B。
9. 解析：
地磁场垂直分量$$B_\perp = B\sin30° = \frac{B}{2}$$，安培力$$F = B_\perp IL = \frac{1}{2}BIL$$。答案为 B。
10. 解析：
根据对称性，$$A$$和$$B$$导线在$$O$$点的磁场抵消，$$C$$导线在$$O$$点产生沿$$x$$轴负方向的磁场。$$O$$导线电流向外，受安培力方向沿$$y$$轴正方向（左手定则）。答案为 A。