.jpg)
正确率80.0%
电磁炮是利用电磁发射技术制成的新型武器，如图所示为电磁炮的原理结构示意图。若某水平发射轨道长$${{7}{.}{5}{m}}$$，宽$${{1}{.}{5}{m}}$$，发射的炮弹质量为$${{5}{0}{g}}$$，炮弹被发射时从轨道左端由静止开始加速。当电路中的电流恒为$${{2}{0}{A}}$$时，炮弹被发射后的最大速度可达$$3 \times1 0^{3} m / s$$，轨道间磁场为匀强磁场，不计空气及摩擦阻力。下列说法正确的是$${{(}{)}}$$
A.磁场方向为竖直向下
B.磁场方向为水平向右
C.磁场的磁感应强度大小为$${{1}{×}{{1}{0}^{3}}{T}}$$
D.炮弹的加速度大小为$$3 \times1 0^{5} \， m / s^{2}$$
2、['磁场对通电导线的作用力'， '传动问题'， '安培力的方向判断（左手定则）']正确率80.0%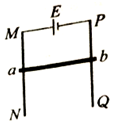
如图所示，$${{M}{N}}$$、$${{P}{Q}}$$为竖直放置的两根平行光滑金属导轨，导轨上端接有电源。现加一匀强磁场，使导体棒$${{a}{b}}$$水平静止在金属导轨上，并与导轨接触良好。则所加匀强磁场的方向可能为$${{(}{)}}$$
C
A.水平向左
B.水平向右
C.垂直纸面向里
D.垂直纸面向外
3、['磁场对通电导线的作用力'， '导体棒或线圈切割磁感线时引起的感应电动势及计算']正确率40.0%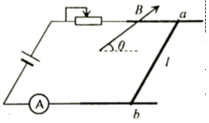
如图所示，两平行金属导轨处于同一水平面内，在两导轨一端上放置一质量为$${{m}}$$、长度为$${{l}}$$的金属杆$${{a}{b}}$$，两导轨的另一端与电源、滑动变阻器、电流表构成闭合回路。整个装置处在磁感应强度为$${{B}}$$的匀强磁场中，磁场方向与导轨半面成$${{θ}{=}{{3}{7}}{°}}$$角斜向上。刚开始，滑动变阻器连入电路的电阻最大，$${{a}{b}}$$静止在水平导轨上，调节滑动变阻器滑片的位置，发现当电流表的示数为$${{I}}$$时，金属杆$${{a}{b}}$$刚要开始滑动，已知金属杆与导导轨间的滑动摩擦力近似等于它们之间的最大静摩擦力，$$\operatorname{s i n} 3 7^{\circ}=0. 6$$，$$\operatorname{c o s} 3 7^{\circ}=0. 8$$。则金属杆与导轨间的动摩擦因数为$${{(}{)}}$$
D
A.$$\frac{B \varPi} {m g}$$
B.$$\frac{4 B I l} {5 m g-3 B I l}$$
C.$$\frac{3 B I l} {5 m g+4 B I l}$$
D.$$\frac{3 B \mathit{I} \mathit{l}} {5 m g-4 B \mathit{I} \mathit{l}}$$
4、['安培力的大小简单计算及应用'， '磁场对通电导线的作用力'， '电阻定律']正确率40.0%
如图，同种材料制成的粗细均匀半圆形单匝导线框$${{M}{P}{N}}$$固定于匀强磁场中，线框平面与磁场方向垂直，直径$${{M}{N}}$$两端与直流电源相接。已知$${{M}{N}}$$段所受安培力大小为$${{F}}$$，忽略电流之间的相互作用。则$${{(}{)}}$$
A.$${{M}{N}}$$段所受安培力的方向直于线框平面
B.通过$${{M}{N}}$$段与$$\overbrace{M P N}$$段的电流之比为$$I_{M N} \colon\， I_{\overline{{M N P}}}=2$$：$${{π}}$$
C.$$\overbrace{M P N}$$段所受安培力大小为$$\frac{2 F} {\pi}$$
D.半圆形线框所受安培力大小为$$\frac{( \pi-2 ) F} {\pi}$$
5、['磁场对通电导线的作用力'， '安培力的大小简单计算及应用'， '闭合电路的欧姆定律']正确率80.0%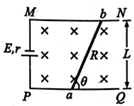
如图，水平固定导轨$${{M}{N}}$$、$${{P}{Q}}$$间距为$${{L}}$$；左侧$${{M}{P}}$$间接有电动势为$${{E}}$$、内阻为$${{r}}$$的电源，整个装置处在磁感应强度大小为$${{B}}$$、方向垂直于导轨平面向下的匀强磁场中。一阻值为$${{R}}$$的金属棒$${{a}{b}}$$与导轨间成$${{θ}}$$角搁置于导轨上而静止，金属棒$${{a}{b}}$$与导轨接触良好，不计其他电阻。下列说法正确的是$${{(}{)}}$$
A.金属棒$${{a}{b}}$$受到的安培力方向沿导轨向左
B.金属棒$${{a}{b}}$$受到的摩擦力方向沿导轨向右
C.金属棒$${{a}{b}}$$受到的摩擦力大小为$$\frac{B E L} {R+r}$$
D.金属棒$${{a}{b}}$$受到的安培力大小为$$\frac{B E L} {( R+r ) \operatorname{s i n} \theta}$$
6、['磁场对通电导线的作用力'， '闭合电路的欧姆定律'， '电磁感应中的功能问题'， '法拉第电磁感应定律的表述及表达式'， '导体棒或线圈切割磁感线时引起的感应电动势及计算']正确率80.0%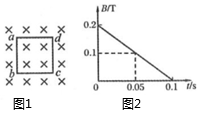
如图所示，垂直于纸面向里的匀强磁场，磁感应强度$${{B}}$$随时间$${{t}}$$均匀变化，磁场方向取垂直纸面向里为正方向。正方形硬质金属框$${{a}{b}{c}{d}}$$放置在磁场中，金属框平面与磁场方向垂直，电阻$${{R}{=}{{0}{.}{1}}{Ω}}$$，边长$${{l}{=}{{0}{.}{2}}{m}}$$。则下列说法错误的是$${{(}{)}}$$
C
A.在$${{t}{=}{0}}$$到$${{t}{=}{{0}{.}{1}}{s}}$$时间内，金属框中的感应电动势为$$0. 0 8 V$$
B.在$${{t}{=}{{0}{.}{0}{5}}{s}}$$时，金属框$${{a}{b}}$$边受到的安培力的大小为$$0. 0 1 6 N$$
C.在$${{t}{=}{{0}{.}{0}{5}}{s}}$$时，金属框$${{a}{b}}$$边受到的安培力的方向垂直于$${{a}{b}}$$向右
D.在$${{t}{=}{0}}$$到$${{t}{=}{{0}{.}{1}}{s}}$$时间内，金属框中电流的电功率为$$0. 0 6 4 W$$
7、['磁场对通电导线的作用力'， '闭合电路的欧姆定律'， '导体棒或线圈切割磁感线时引起的感应电动势及计算']正确率40.0%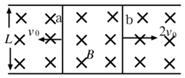
如图所示，两电阻可以忽略不计的平行金属长直导轨固定在水平面上，相距为$${{L}}$$，另外两根长度为$${{L}}$$、质量为$${{m}}$$、电阻为$${{R}}$$的相同导体棒垂直静置于导轨上，导体棒在长导轨上可以无摩擦地左右滑动，导轨间存在竖直向下的匀强磁场，磁感应强度大小为$${{B}}$$。某时刻使左侧的导体棒获得大小为$${{v}_{0}}$$的向左初速度、右侧的导体棒获得大小为$${{2}{{v}_{0}}}$$的向右初速度，则下列结论正确的是$${{(}{)}}$$
C
A.该时刻回路中产生的感应电动势为$${{B}{L}{{v}_{0}}}$$
B.当导体棒$${{a}}$$的速度大小为$$\frac{v_{0}} {2}$$时，导体棒$${{b}}$$的速度大小一定是$$\frac{3 v_{0}} {2}$$
C.当导体棒$${{a}}$$的速度为$${{0}}$$时，两导体棒受到的安培力大小都是$$\frac{B^{2} L^{2} v_{0}} {2 R}$$
D.当导体棒$${{a}}$$的速度为$${{0}}$$时，两导体棒受到的安培力大小都是$$\frac{B^{2} L^{2} v_{0}} {R}$$
8、['磁场对通电导线的作用力'， '闭合电路的欧姆定律'， '电磁感应中的功能问题'， '导体棒或线圈切割磁感线时引起的感应电动势及计算'， '电功与电功率定义、表达式、物理意义及简单应用']正确率40.0%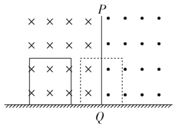
在光滑的水平面上方，有两个磁感应强度大小均为$${{B}}$$、方向相反的水平匀强磁场，如图。$${{P}{Q}}$$为两个磁场的边界，磁场范围足够大。一个边长为$${{a}}$$、质量为$${{m}}$$、电阻为$${{R}}$$的金属正方形线框，以速度$${{v}}$$垂直磁场方向从如图实线位置开始向右运动，当线框运动到分别有一半面积在两个磁场中时，线框的速度为$$\frac{v} {2}$$，则下列说法正确的是$${{(}{)}}$$
D
A.此过程中通过线框截面的电量为$$\frac{2 B a^{2}} {R}$$
B.此时线框的加速度为$$\frac{B^{2} a^{2} v} {2 m R}$$
C.此过程中回路产生的电能为$${\frac{1} {8}} m v^{2}$$
D.此时线框中的电功率为$$\frac{B^{2} a^{2} v^{2}} {R}$$
9、['磁场对通电导线的作用力'， '物体的共点力平衡']正确率80.0%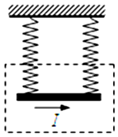
用两个一样的弹簧吊着一根铜棒，铜棒所在虚线范围内有垂直于纸面的匀强磁场，棒中通以自左向右的电流$${{(}}$$如图所示$${{)}}$$，当棒静止时，两弹簧的拉力大小分别为$${{F}_{1}}$$；若将棒中的电流方向反向$${{(}}$$大小保持不变$${{)}}$$，当棒静止时，两弹簧的拉力大小分别为$${{F}_{2}}$$，且$${{F}_{2}{>}{{F}_{1}}}$$。根据以上信息，可以确定$${{(}{)}}$$
D
A.磁感应强度的大小
B.电流强度的大小
C.铜棒的长度与电流的乘积
D.磁场的方向
10、['磁场对通电导线的作用力'， '功率']正确率0.0%电磁炮是一种理想的兵器，它的主要原理如图所示，利用这种装置可以把质量为$${{m}{=}{{2}{.}{0}}{g}}$$的弹体$${{(}}$$包括金属杆$${{E}{F}}$$的质量$${{)}}$$加速到$$6 k m / s$$，若这种装置的轨道宽为$${{d}{=}{2}{m}}$$，长$${{L}{=}{{1}{0}{0}}{m}}$$，电流$${{I}{=}{{1}{0}}{A}}$$，轨道摩擦不计且金属杆$${{E}{F}}$$与轨道始终接触良好，则下列有关轨道问所加匀强磁场的磁感应强度和磁场力的最大功率结果正确的是$${{(}}$$$${{)}}$$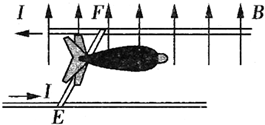
A.$${{B}{=}{{1}{8}}}$$$${{T}}$$，$$P_{m}=1. 0 8 \times1 0^{8} W$$
B.$${{B}{=}{{0}{.}{6}}}$$$${{T}}$$，$$P_{m}=7. 2 \times1 0^{4} \， W$$
C.$${{B}{=}{{0}{.}{6}}}$$$${{T}}$$，$$P_{m}=3. 6 \times1 0^{6} \， W$$
D.$${{B}{=}{{1}{8}}}$$$${{T}}$$，$$P_{m}=2. 1 6 \times1 0^{6} \， W$$
1. 解析：电磁炮的安培力方向由左手定则判断。炮弹向右加速，电流方向垂直于纸面向里，故磁场方向应竖直向上（题目无此选项，可能题目描述有误）。根据动能定理 $$Fd = \frac{1}{2}mv^2$$，安培力 $$F = BIL$$，代入数据得 $$B = \frac{mv^2}{2ILd} = \frac{0.05 \times (3 \times 10^3)^2}{2 \times 20 \times 1.5 \times 7.5} = 1 \times 10^3 \, \text{T}$$。加速度 $$a = \frac{v^2}{2d} = \frac{(3 \times 10^3)^2}{2 \times 7.5} = 6 \times 10^5 \, \text{m/s}^2$$（选项 D 错误）。正确答案为 C。
2. 解析：导体棒静止时，安培力需平衡重力。电流方向由 $$a$$ 到 $$b$$，若磁场垂直纸面向里，安培力向左；若垂直纸面向外，安培力向右。水平方向的磁场无法平衡重力。因此可能方向为垂直纸面向里或向外，选项 C 和 D 正确。
3. 解析：金属杆受力平衡时，安培力水平分量为 $$F_x = BIl \cos 37^\circ$$，垂直分量为 $$F_y = BIl \sin 37^\circ$$。摩擦力 $$f = \mu (mg - F_y)$$，当 $$f = F_x$$ 时开始滑动，解得 $$\mu = \frac{BIl \cos 37^\circ}{mg - BIl \sin 37^\circ} = \frac{4BIl}{5mg - 3BIl}$$，选项 B 正确。
4. 解析：$$MN$$ 段安培力方向垂直于线框平面向外（选项 A 错误）。半圆形导线电阻是 $$MN$$ 段的 $$\pi/2$$ 倍，电流比为 $$2:\pi$$（选项 B 正确）。$$\overbrace{MPN}$$ 段等效长度为直径，安培力为 $$F_{MPN} = BIL_{eff} = BI \cdot \frac{2l}{\pi} = \frac{2F}{\pi}$$（选项 C 正确）。总安培力为 $$F - \frac{2F}{\pi} = \frac{(\pi - 2)F}{\pi}$$（选项 D 正确）。
5. 解析：电流方向由 $$a$$ 到 $$b$$，安培力方向垂直于棒向左下方（选项 A 错误）。摩擦力平衡安培力水平分量，方向向右（选项 B 正确）。安培力大小 $$F = BIL = \frac{BEL}{R + r}$$，摩擦力 $$f = F \sin \theta = \frac{BEL \sin \theta}{R + r}$$（选项 C 错误，D 错误）。
6. 解析：感应电动势 $$E = \frac{\Delta B}{\Delta t} \cdot l^2$$，若 $$B$$ 均匀变化，$$E = 0.08 \, \text{V}$$（选项 A 正确）。安培力 $$F = BIl$$，$$t = 0.05 \, \text{s}$$ 时 $$B$$ 未知，无法计算（选项 B 错误）。由楞次定律知安培力方向垂直于 $$ab$$ 向右（选项 C 正确）。电功率 $$P = \frac{E^2}{R} = 0.064 \, \text{W}$$（选项 D 正确）。题目要求选错误选项，故答案为 B。
7. 解析：初始感应电动势 $$E = BL(v_0 + 2v_0) = 3BLv_0$$（选项 A 错误）。动量守恒 $$mv_0 - 2mv_0 = -mv_a + mv_b$$，当 $$v_a = v_0/2$$ 时 $$v_b = 3v_0/2$$（选项 B 正确）。当 $$v_a = 0$$ 时 $$v_b = v_0$$，安培力 $$F = \frac{B^2 L^2 v_0}{2R}$$（选项 C 正确）。
8. 解析：通过线框的电量 $$q = \frac{\Delta \Phi}{R} = \frac{2Ba^2}{R}$$（选项 A 正确）。此时感应电动势 $$E = 2Bav/2 = Bav$$，电流 $$I = Bav/R$$，安培力 $$F = 2BIa = 2B^2 a^2 v / R$$，加速度 $$a = F/m = 2B^2 a^2 v / mR$$（选项 B 错误）。能量守恒得电能 $$E = \frac{1}{2}mv^2 - \frac{1}{2}m(v/2)^2 = \frac{3}{8}mv^2$$（选项 C 错误）。电功率 $$P = I^2 R = \frac{B^2 a^2 v^2}{R}$$（选项 D 正确）。
9. 解析：由 $$F_2 > F_1$$ 知安培力方向向下，磁场方向垂直纸面向里（选项 D 正确）。安培力 $$F = BIL$$，但无法单独确定 $$B$$、$$I$$ 或 $$L$$（选项 A、B 错误），只能确定 $$BIL$$ 的乘积（选项 C 正确）。
10. 解析：由动能定理 $$F \cdot L = \frac{1}{2}mv^2$$，安培力 $$F = BId$$，得 $$B = \frac{mv^2}{2IdL} = \frac{0.002 \times (6000)^2}{2 \times 10 \times 2 \times 100} = 1.8 \, \text{T}$$。最大功率 $$P_m = Fv = BIdv = 1.8 \times 10 \times 2 \times 6000 = 2.16 \times 10^5 \, \text{W}$$（选项 D 正确）。