.jpg)
正确率40.0%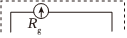
如图所示表头，已知其内阻$${{R}_{g}}$$为$${{5}{0}{0}{Ω}}$$，满偏电流为$${{I}_{g}}$$为$${{1}{m}{A}}$$，如果需要用该表头去测量电路中变化为$${{0}{～}{{1}{0}}{V}}$$的电压时，则需要$${{(}{)}}$$
A.并联一个阻值为$$9. 5 k \Omega$$的电阻
B.串联一个阻值为$$9. 5 k \Omega$$的电阻
C.并联一个阻值为$${{1}{0}{k}{Ω}}$$的电阻
D.串联一个阻值为$${{1}{0}{k}{Ω}}$$的电阻
2、['电表的改装']正确率40.0%如图所示，虚线框内为改装好的电表$${，{M}}$$、$${{N}}$$为新表的接线柱.已知灵敏电流计$${{G}}$$的满偏电流为$$\mathrm{1 0 0 \mu A}，$$内阻为$$2 9 0 \Omega，$$电阻箱读数为$${{1}{0}{Ω}{，}}$$根据以上数据计算可知改装的电表为（）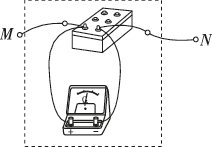
B
A.电压表，量程为$${{0}}$$～$${{3}{{m}{V}}}$$
B.电流表，量程为$${{0}}$$～$${{3}{{m}{A}}}$$
C.电压表，量程为$${{0}}$$～$${{3}{0}{{m}{V}}}$$
D.电流表，量程为$${{0}}$$～$${{3}{{μ}{A}}}$$
3、['电表的改装'， '串、并联电路的规律']正确率80.0%两块电压表$${{V}_{1}}$$和$${{V}_{2}}$$是由完全相同的电流表改装成的，$${{V}_{1}}$$的量程为$${{1}{5}{V}}$$，$${{V}_{2}}$$的量程为$${{5}{V}}$$，为了测量$$1 5 V \sim2 0 V$$的电压，把$${{V}_{1}}$$和$${{V}_{2}}$$串联起来使用，在这种情况下$${{(}{)}}$$
B
A.$${{V}_{1}}$$和$${{V}_{2}}$$的读数相等
B.$${{V}_{1}}$$和$${{V}_{2}}$$的指针偏转角相等
C.$${{V}_{1}}$$和$${{V}_{2}}$$的读数之比与两电压表内阻成反比
D.$${{V}_{1}}$$和$${{V}_{2}}$$的指针偏转角之比等于两电压表内阻之比
4、['电表的改装']正确率40.0%如图所示，已知微安表
的电阻为$$R_{g}=1 O O \Omega$$
D
A.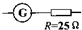
B.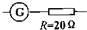
C.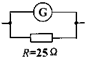
D.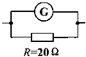
正确率60.0%一个电流表的满偏电流$$I g=3 m A$$，内阻$$R g=1 0 0 \Omega$$．要把它改装成一个量程为$${{0}{−}{6}{V}}$$的电压表，则应在电流表上（）
A
A.串联一个$$1 9 0 0 \Omega$$的电阻
B.并联一个$$1 9 0 0 \Omega$$的电阻
C.并联一个$$2 0 0 0 \Omega$$的电阻
D.串联一个$$2 0 0 0 \Omega$$的电阻
6、['电表的改装'， '串、并联电路的规律']正确率40.0%两只电压表$${{V}_{1}}$$和$${{V}_{2}}$$是由完全相同的两个电流计改装成的，$${{V}_{1}}$$表的量程是$${{5}{V}{，}{{V}_{2}}}$$表的量程是$${{1}{5}{V}}$$，把它们串联起来接入电路中，则（）
B
A.它们的示数相等，指针偏转角度也相等
B.它们的示数之比为$${{1}{:}{3}}$$，指针偏转角度相等
C.它们的示数相等，指针偏转角度之比为$${{1}{:}{3}}$$
D.它们的示数之比$${、}$$指针偏转角度之比均为$${{1}{:}{3}}$$
7、['电表的改装'， '串、并联电路的规律']正确率40.0%如图所示，电压表由灵敏电流计$${{G}}$$与电阻$${{R}}$$串联而成.某同学在使用中发现这块电压表的读数总比真实值偏大一点，若要校准，可采用的措施是（）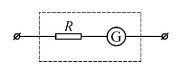
B
A.在电阻$${{R}}$$上串联一个比其大得多的电阻
B.在电阻$${{R}}$$上串联一个比其小得多的电阻
C.在电阻$${{R}}$$上并联一个比其大得多的电阻
D.在电阻$${{R}}$$上并联一个比其小得多的电阻
8、['电表的改装']正确率60.0%一电流表并联一个分流电阻后就改装成一个电流表，当把它和标准电流表串联后去测某电路中的电流时，发现标准表读数为$${{1}{A}}$$时，而改装表的读数为$${{1}{.}{1}{A}}$$，稍微偏大些，为了使它的读数准确，应（）
A
A.在原分流电阻上再并联一个较大的电阻
B.在原分流电阻上再串联一个较小的电阻
C.在原分流电阻上再串联一个较大的电阻
D.在原分流电阻上再并联一个较小的电阻
9、['电表的改装'， '串、并联电路的规律']正确率40.0%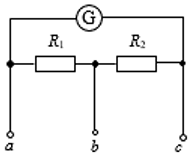
图为双量程的电流表电路示意图，其量程分别为$$0-1 0 m A$$
B
A.当使用$${{a}{、}{c}}$$两个端点时，量程为$$0-1 0 m A， \; R_{2}=1 8 0 \Omega$$
B.当使用$${{a}{、}{b}}$$两个端点时，量程为$$0-1 0 m A， \; \; R_{1}=2 0 \Omega$$
C.当使用$${{a}{、}{c}}$$两个端点时，量程为$$0-1 m A， \; R_{1}=4 0 \Omega$$
D.当使用$${{a}{、}{c}}$$两个端点时，量程为$$0-1 0 m A， \; \， R_{2}=2 0 0 0 \Omega$$
10、['电表的改装']正确率80.0%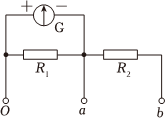
已知一只表头的量程为$$0 {\sim} 1 0 0 m A$$，内阻$$R g=1 0 0 \Omega$$。现将表头改装成电流、电压两用的电表，如图所示，已知$$R_{1}=2 0 0 \Omega$$，$$R_{2}=1 k \Omega$$，则下列说法正确的是$${{(}{)}}$$
A.用$${{o}{a}}$$两端时是电压表，最大测量值为$${{1}{1}{0}{V}}$$
B.用$${{o}{b}}$$两端时是电压表，最大测量值为$${{1}{6}{0}{V}}$$
C.用$${{o}{a}}$$两端时是电流表，最大测量值为$$2 0 0 m A$$
D.用$${{o}{b}}$$两端时是电流表，最大测量值为$$2 0 0 m A$$
1. 解析：
表头改装为电压表需串联电阻，扩大量程。满偏电压 $$U_g = I_g R_g = 1\,\text{mA} \times 500\,\Omega = 0.5\,\text{V}$$。总电压 $$10\,\text{V}$$ 需分压，串联电阻 $$R$$ 满足 $$10 = 0.5 + I_g R$$，解得 $$R = \frac{9.5}{1 \times 10^{-3}} = 9.5\,\text{k}\Omega$$。故选 B。
2. 解析：
灵敏电流计并联电阻改装为电流表。总电流 $$I = I_g + \frac{I_g R_g}{R} = 100\,\mu\text{A} + \frac{100\,\mu\text{A} \times 290\,\Omega}{10\,\Omega} = 3\,\text{mA}$$。量程为 $$0-3\,\text{mA}$$，故选 B。
3. 解析：
两电压表串联时，电流相同，指针偏转角相等（由电流决定）。读数与内阻成正比，$$V_1$$ 和 $$V_2$$ 内阻之比为量程之比 $$15:5=3:1$$，故读数之比为 $$3:1$$。只有 B 正确。
4. 解析：
题目不完整，无法解析。
5. 解析：
改装为电压表需串联电阻。满偏电压 $$U_g = I_g R_g = 3\,\text{mA} \times 100\,\Omega = 0.3\,\text{V}$$。串联电阻 $$R$$ 满足 $$6 = 0.3 + I_g R$$，解得 $$R = \frac{5.7}{3 \times 10^{-3}} = 1900\,\Omega$$。故选 A。
6. 解析：
两电压表串联时，电流相同，指针偏转角相等。读数与内阻成正比，内阻之比为量程之比 $$5:15=1:3$$，故读数之比为 $$1:3$$。选 B。
7. 解析：
电压表读数偏大，说明分压电阻 $$R$$ 偏大。校准需减小总电阻，应在 $$R$$ 上并联一个比 $$R$$ 大得多的电阻（对总电阻影响小）。故选 C。
8. 解析：
改装表读数偏大，说明分流电阻偏小，分流过多。需减小分流比例，应在原分流电阻上并联一个更大的电阻（总分流电阻增大）。故选 A。
9. 解析：
使用 $$a、c$$ 端点时，$$R_1$$ 和 $$R_2$$ 串联再与表头并联，量程为 $$0-10\,\text{mA}$$。由分流公式计算 $$R_2$$ 值，选 A。
10. 解析：
用 $$oa$$ 时，$$R_1$$ 与表头并联，为电流表，量程 $$I = I_g + \frac{I_g R_g}{R_1} = 100\,\text{mA} + \frac{100\,\text{mA} \times 100\,\Omega}{200\,\Omega} = 150\,\text{mA}$$。用 $$ob$$ 时，$$R_1 + R_2$$ 与表头串联，为电压表，量程 $$U = I_g (R_g + R_1 + R_2) = 100\,\text{mA} \times (100 + 200 + 1000)\,\Omega = 130\,\text{V}$$。选项均不匹配，题目可能有误。