.jpg)
正确率19.999999999999996%一个质量为$${{m}}$$，电荷量为$${{+}{q}}$$的小球在方向竖直的匀强电场中足够高处由静止释放，电场强度按图示的$${{E}{−}{t}}$$图线变化，$$E_{0}={\frac{2 m g} {q}}$$，竖直向上为正方向，下列说法中正确的是（）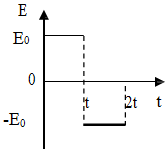
C
A.$${{0}{−}{2}{t}}$$内，小球所受到合外力的冲量为零
B.$${{0}{−}{2}{t}}$$内，小球所受重力的冲量为零
C.$${{0}{−}{2}{t}}$$内，重力对小球做功为零
D.$${{0}{−}{2}{t}}$$内，小球的电势能先减小后增大
2、['匀强电场中电势差与电场强度的关系'， '带电粒子在交变电场中的运动'， '电场强度的表达式和单位'， '运用牛顿第二定律分析动态过程']正确率40.0%从$${{t}{=}{0}}$$时刻起，在两块平行金属板间分别加上如图所示的交变电压，加其中哪种交变电压时，原来处于两板正中央的静止电子不可能在两板间做往复运动（）
D
A.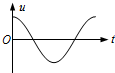
B.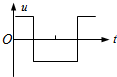
C.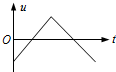
D.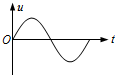
正确率40.0%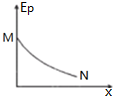
$${{M}{、}{N}}$$
A
A.电子在$${{N}}$$点动能大于在$${{M}}$$点动能
B.该电场可能是匀强电场
C.该电子运动的加速度越来越大
D.电子运动的轨迹为曲线
4、['带电粒子在交变电场中的运动'， '从受力确定运动情况']正确率40.0%如图甲所示，在两极板 $${{a}}$$ $${、{b}}$$之间有一静止的电子，当在 $${{a}}$$ $${、{b}}$$之间加上如图乙所示的变化电压时(开始时 $${{a}}$$板带正电$${{)}}$$，电子的运动情况是(不计重力，板间距离足够大 $${{a}{b}}$$上电压大小不变$${{)}{（}}$$）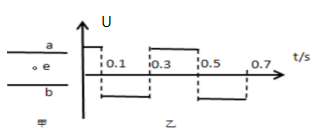
D
A.电子一直向 $${{a}}$$板运动
B.电子一直向 $${{b}}$$板运动
C.电子先向 $${{a}}$$板运动，再返回，最终必打在 $${{b}}$$板上
D.电子在两板间做周期性往返运动
5、['带电粒子在交变电场中的运动'， '从受力确定运动情况'， '牛顿第二定律的简单应用']正确率40.0%如图，$${{A}}$$板的电势$$\varphi_{A}=0， ~ U_{A B}$$随时间的变化规律如图所示，且$${{A}{B}}$$板间的距离足够大。某电子只受电场力的作用，且初速度为零，则下列说法错误的是（）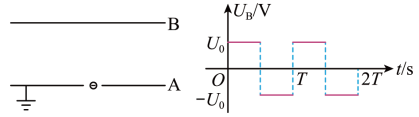
D
A.若电子在$${{t}{=}{0}}$$时刻进入的，它将一直向$${{B}}$$板运动
B.若电子在$$t=\frac{T} {8}$$时刻进入的，它将时而向$${{B}}$$板运动，时而向$${{A}}$$板运动，最后打在$${{B}}$$板上
C.若电子在$$t=\frac{T} {2}$$时刻进入的，它将时而向$${{B}}$$板$${、}$$时而向$${{A}}$$板运动
D.若电子是在$$t=\frac{2 T} {3}$$时刻进入的，它将时面向$${{B}}$$板运动，时而向$${{A}}$$板运动，最后打在$${{B}}$$板上
6、['带电粒子在交变电场中的运动'， '带电粒子在电场中的直线运动']正确率40.0%如图所示的交变电压加在平行板电容器$${{A}}$$、$${{B}}$$两极板上$${，{t}{=}{0}}$$时$${{B}}$$板电势比$${{A}}$$板电势高，这时有一个原来静止的电子正处在两板的中间，它在静电力作用下开始运动.设$${{A}}$$、$${{B}}$$两极板间的距离足够大，下列说法正确的是（）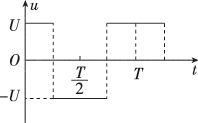
D
A.电子一直向着$${{A}}$$板运动
B.电子一直向着$${{B}}$$板运动
C.电子先向$${{A}}$$板运动，然后返回向$${{B}}$$板运动，之后在$${{A}}$$、$${{B}}$$两板间做周期性往复运动
D.电子先向$${{B}}$$板运动，然后返回向$${{A}}$$板运动，之后在$${{A}}$$、$${{B}}$$两板间做周期性往复运动
7、['带电粒子在交变电场中的运动'， '带电粒子在电场中的直线运动']正确率40.0%如图甲所示，两平行正对的金属板$${{A}{、}{B}}$$间加有如图乙所示的交变电压，一重力可忽略不计的带正电粒子被固定在两板的正中间$${{P}}$$处。若在$${{t}_{0}}$$时刻释放该粒子，粒子会时而向$${{A}}$$板运动，时而向$${{B}}$$板运动，并最终打在$${{A}}$$板上。则$${{t}_{0}}$$可能属于的时间段是（）
B
A.$$0 < t_{0} < \frac{T} {4}$$
B.$$\frac{T} {2} < t_{0} < \frac{3 T} {4}$$
C.$${\frac{3 T} {4}} < t_{0} < T$$
D.$$T < t_{0} < \frac{9 T} {8}$$
8、['带电粒子在交变电场中的运动']正确率40.0%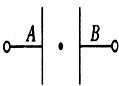
如图所示，在两平行金属板中央有一个静止的电子(不计重力$${{)}}$$
B
A.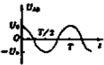
B.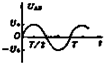
C.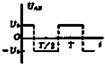
D.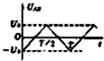
正确率40.0%如图所示，两块平行金属板$${{M}{N}}$$间的距离为$${{d}}$$，两板间电压$${{u}}$$随时间$${{t}}$$变化的规律如图所示电压的绝对值为$$U_{0}， ~ t \mathrm{=} 0$$时刻$${{M}}$$板的电势比$${{N}}$$板低。在$${{t}{=}{0}}$$时刻有一个电子从$${{M}}$$板处无初速释放，并在$${{t}{=}{2}{T}}$$时刻恰好到达$${{N}}$$板$${{.}}$$电子的电荷量为$${{e}}$$，下列说法正确的是（）
B
A.$$t=\frac{T} {4}$$时刻释放电子，电子将一直向$${{N}}$$板运动，最终到达$${{N}}$$板
B.$$t=\frac{T} {3}$$时刻释放电子，电子先向$${{N}}$$板运动，后反向运动，最终到达$${{M}}$$板
C.$$t=\frac{3} {8} T$$时刻释放电子，电子时而向$${{N}}$$板运动，时而向$${{M}}$$板运动，最终到达$${{N}}$$板
D.在$$t=\frac{T} {6}$$时刻释放电子，$${\frac{3 7} {6} T}$$时刻到达$${{N}}$$板
10、['带电粒子在交变电场中的运动'， '带电粒子在电场中的直线运动']正确率40.0%如图$${{1}}$$所示，在两平行金属板中央有一个静止的电子$${{(}}$$不计重力$${{)}}$$，当两板间的电压分别如图$${{2}}$$中甲、乙、丙、丁所示时，电子在板间运动$${{(}}$$假设不与板相碰$${{)}}$$，下列说法正确的是$${{(}{)}}$$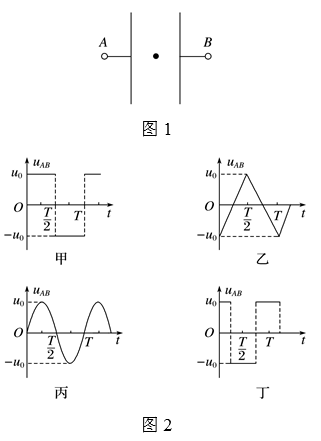
D
A.电压是甲图时，在$${{0}{～}{T}}$$时间内，电子的电势能一直减少
B.电压是乙图时，在$$0 \sim\frac{T} {2}$$时间内，电子的电势能先增加后减少
C.电压是丙图时，电子在板间做往复运动
D.电压是丁图时，电子在板间做往复运动
1. 解析：
电场强度 $$E_0 = \frac{2mg}{q}$$，方向竖直向上。小球受力分析：
- $$0 \leq t \leq t$$：电场向上，$$F_{电} = qE_0 = 2mg$$，合外力 $$F = F_{电} - mg = mg$$ 向上，加速度 $$a = g$$ 向上。
- $$t \leq t \leq 2t$$：电场向下，$$F_{电} = -qE_0 = -2mg$$，合外力 $$F = F_{电} - mg = -3mg$$ 向下，加速度 $$a = -3g$$ 向下。
速度变化：
- $$t$$ 时刻速度 $$v_1 = gt$$ 向上。
- $$2t$$ 时刻速度 $$v_2 = v_1 - 3gt = -2gt$$ 向下。
选项分析：
- A：合外力冲量 $$I = \Delta p = m(v_2 - 0) = -2mgt \neq 0$$，错误。
- B：重力冲量 $$I_g = mg \cdot 2t \neq 0$$，错误。
- C：重力做功 $$W_g = mg \cdot \Delta h$$，$$0-2t$$ 内位移向下，重力做正功，错误。
- D：$$0-t$$ 电场力做正功，电势能减小；$$t-2t$$ 电场力做负功，电势能增大，正确。
答案：D
2. 解析：
电子在交变电场中受力 $$F = -eE$$，加速度 $$a = -\frac{eU}{md}$$。做往复运动的条件是电压对称且周期性变化。
- A：电压对称，电子做往复运动。
- B：电压不对称，电子单向加速，不可能往复运动。
- C：电压对称，电子做往复运动。
- D：电压对称，电子做往复运动。
答案：B
3. 解析：
电场线从 $$M$$ 指向 $$N$$，电子受力方向与电场线相反，从 $$N$$ 向 $$M$$ 加速运动。
- A：电子从 $$N$$ 到 $$M$$ 加速，动能增大，$$N$$ 点动能小于 $$M$$ 点，错误。
- B：电场线疏密变化，非匀强电场，错误。
- C：电场线变密，场强增大，加速度增大，正确。
- D：电子初速度方向与受力方向共线，轨迹为直线，错误。
答案：C
4. 解析：
电子受力方向与电场方向相反：
- $$0 \leq t \leq T/2$$：$$a$$ 板正，电子向 $$b$$ 板加速。
- $$T/2 \leq t \leq T$$：$$a$$ 板负，电子向 $$a$$ 板减速，但未返回原点。
- 后续周期重复，电子单向运动。
答案：B
5. 解析：
电子受力方向与电场方向相反：
- A：$$t=0$$ 进入，$$0-T/2$$ 向 $$B$$ 加速，$$T/2-T$$ 减速但未返回，正确。
- B：$$t=T/8$$ 进入，前半周期向 $$B$$ 加速，后半周期减速但未返回原点，最终打在 $$B$$ 板，正确。
- C：$$t=T/2$$ 进入，$$T/2-T$$ 向 $$A$$ 加速，$$T-3T/2$$ 向 $$B$$ 减速，往复运动，正确。
- D：$$t=2T/3$$ 进入，$$2T/3-T$$ 向 $$A$$ 加速，$$T-4T/3$$ 向 $$B$$ 减速，最终打在 $$A$$ 板，错误。
答案：D
6. 解析：
电子受力方向与电场方向相反：
- $$0 \leq t \leq T/2$$：$$B$$ 板正，电子向 $$A$$ 板加速。
- $$T/2 \leq t \leq T$$：$$B$$ 板负，电子向 $$B$$ 板减速并返回。
- 后续周期重复，电子往复运动。
答案：D
7. 解析：
粒子最终打在 $$A$$ 板，说明向 $$A$$ 板位移更大。分析 $$t_0$$ 时刻释放：
- A：$$0 < t_0 < T/4$$，前半周期向 $$A$$ 加速时间长，可能。
- B：$$T/2 < t_0 < 3T/4$$，前半周期向 $$B$$ 加速，后半周期向 $$A$$ 减速，可能。
- C：$$3T/4 < t_0 < T$$，前半周期向 $$A$$ 加速时间短，可能。
- D：$$T < t_0 < 9T/8$$，超出周期范围，无意义。
答案：B
8. 解析：
电子受力方向与电场方向相反：
- A：$$0-T/2$$ 向 $$B$$ 加速，$$T/2-T$$ 向 $$A$$ 减速，往复运动。
- B：$$0-T/2$$ 向 $$B$$ 加速，$$T/2-T$$ 向 $$A$$ 减速，往复运动。
- C：$$0-T/2$$ 向 $$B$$ 加速，$$T/2-T$$ 向 $$A$$ 减速，往复运动。
- D：电压不对称，电子单向运动，不可能往复。
答案：D
9. 解析：
电子运动分析：
- A：$$t=T/4$$ 释放，$$T/4-T/2$$ 向 $$N$$ 加速，$$T/2-3T/4$$ 向 $$M$$ 减速，$$3T/4-T$$ 向 $$N$$ 加速，最终到达 $$N$$ 板，正确。
- B：$$t=T/3$$ 释放，$$T/3-T/2$$ 向 $$N$$ 加速，$$T/2-2T/3$$ 向 $$M$$ 减速，$$2T/3-T$$ 向 $$N$$ 加速，最终到达 $$N$$ 板，错误。
- C：$$t=3T/8$$ 释放，$$3T/8-T/2$$ 向 $$N$$ 加速，$$T/2-5T/8$$ 向 $$M$$ 减速，$$5T/8-T$$ 向 $$N$$ 加速，最终到达 $$N$$ 板，正确。
- D：$$t=T/6$$ 释放，$$T/6-T/2$$ 向 $$N$$ 加速，$$T/2-7T/6$$ 向 $$M$$ 减速，$$7T/6-2T$$ 向 $$N$$ 加速，计算位移可判断是否到达 $$N$$ 板。
答案：A、C
10. 解析：
电子运动分析：
- A：甲图 $$0-T$$ 电压恒正，电子向 $$A$$ 加速，电势能一直减少，正确。
- B：乙图 $$0-T/2$$ 电压先正后负，电子先向 $$A$$ 加速后向 $$B$$ 减速，电势能先减少后增加，错误。
- C：丙图电压对称，电子往复运动，正确。
- D：丁图电压不对称，电子单向运动，错误。
答案：A、C