.jpg)
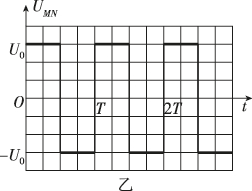
正确率80.0%如图甲所示，某多级直线加速器由$${{n}}$$个横截面积相同的金属圆筒依次排列，其中心轴线在同一直线上，各金属圆筒依序接在交变电源的两极$${{M}}$$、$${{N}}$$上，序号为$${{0}}$$的金属圆板中央有一个质子源，质子逸出的速度不计$${，{M}}$$、$${{N}}$$两极加上如图乙所示的电压$$U_{M N}，$$一段时间后加速器稳定输出质子流.已知质子质量为$${{m}}$$、电荷量为$${{e}{，}}$$质子通过圆筒间隙的时间不计，且忽略相对论效应，则（）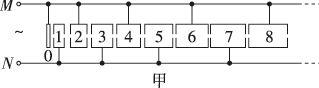
C
A.质子在各圆筒中均做匀加速直线运动
B.质子进入第$${{n}}$$个圆筒瞬间的速率为$$\sqrt{\frac{2 \left( n-1 \right) e U_{0}} {m}}$$
C.各圆筒的长度之比为$${{1}}$$∶$${\sqrt {2}}$$∶$${\sqrt {3}}$$∶…
D.质子在各圆筒中运动的时间之比为$${{1}}$$∶$${\sqrt {2}}$$∶$${\sqrt {3}}$$∶…
2、['动量与能量的其他综合应用'， '牛顿第三定律的内容及理解'， '带电粒子在电场中的直线运动']正确率40.0%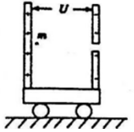
宇宙飞船动力装置的工作原理与下列情景相似：如图，光滑地面上有一质量为$${{M}}$$
C
A.小车总保持静止状态
B.小车最后减速运动
C.粒子穿过小孔时速度为$$\sqrt{\frac{2 M q U} {m ( M+m )}}$$
D.粒子穿过小孔时速度为$$\sqrt{\frac{2 m q U} {M ( M+m )}}$$
3、['回旋加速器'， '带电粒子在电场中的直线运动'， '动能定理的简单应用']正确率19.999999999999996%在高能物理研究中，粒子回旋加速器起着重要作用，左图为其示意图。它由两个$${{D}}$$形盒组成，两个$${{D}}$$形盒正中间开有一条狭缝。两个$${{D}}$$形盒处在匀强磁场中并接有高频交变电压。右图为俯视图，在$${{D}}$$形盒上半面中心$${{S}}$$处有一正粒子源，它发出的正粒子，经狭缝电压加速后，进入$${{D}}$$形盒中。在磁场力的作用下运动半周，再经狭缝电压加速。如此周而复始，最后到达$${{D}}$$形盒的边缘，获得最大速度，由导出装置导出。己知正离子电荷量为$${{q}}$$，质量为$${{m}}$$，加速时电极间电压大小为$${{U}}$$，磁场的磁感应强度大小为$${{B}{，}{D}}$$形盒的半径为$${{R}}$$。每次加速的时间极短，可忽略不计。正粒子从离子源出发时的初速度为零，不计粒子所受重力。则（）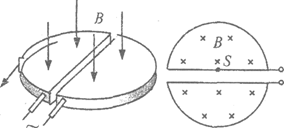
C
A.高频交变电压变化的周期为$$\frac{\pi m} {B q}$$
B.粒子可能获得的最大动能为$$\frac{B q R} {2 m}$$
C.粒子第$${{1}}$$次与第$${{n}}$$次在下半盒中运动的轨道半径之比为$${{1}{:}{\sqrt {{2}{n}{−}{1}}}}$$
D.粒子在回旋加速器中的总的时间为$$\frac{B R^{2}} {2 U}$$
4、['匀强电场中电势差与电场强度的关系'， '带电粒子在电场中的直线运动'， '牛顿第二定律的简单应用'， '动能定理的简单应用']正确率60.0%带等量异种电荷的两块平行金属板间，原来静止的质子和电子分别自正板和负板开始运动，当它们到达对面极板时具有相同的（）
C
A.加速度值
B.速率
C.动能
D.电势能
5、['受力分析'， '带电粒子在电场中的直线运动'， '动能定理的简单应用']正确率40.0%如图所示，一个$${^{4}_{2}{{H}{e}}}$$粒子从平行板电容器的左边由静止释放后，经过一段时间恰好从右极板的小孔进入复合场且沿水平虚线$${{a}{b}}$$向右运动到$${{b}}$$点。不计粒子重力，下列说法正确的是（）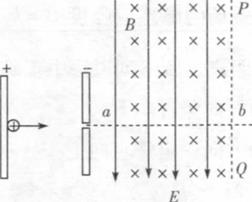
B
A.如果将$${^{4}_{2}{{H}{e}}}$$换成$${^{2}_{1}{H}}$$，粒子在复合场中不能沿直线运动
B.如果将$${^{4}_{2}{{H}{e}}}$$换成$${^{1}_{1}{H}}$$，粒子在复合场中不能沿直线运动
C.无论换成什么样的带电粒子，带电粒子都能沿直线运动
D.如果增大平行板电容器两板的电压，$${^{4}_{2}{{H}{e}}}$$粒子仍能沿直线运动
6、['带电粒子在电场中的直线运动'， '带电粒子在电场中的曲线运动'， '动能定理的简单应用']正确率40.0%如图，水平放置的平行金属板$${{A}{、}{B}}$$间有一匀强电场，一个质子$${{(}{^{1}_{1}}{H}{)}}$$和一个氘核$${{(}{^{2}_{1}}{H}{)}}$$，先后以平行于两板中心线$${{O}{O}{^{′}}}$$的初速度从左侧$${{O}}$$点射入两板间，与板无碰撞且射出后都能击中竖直荧光屏$${{M}{N}}$$，击中荧光屏时的速率分别用$$\upsilon_{\pi\mp}$$和$$\boldsymbol{v}_{\pi}$$表示。下列说法正确的是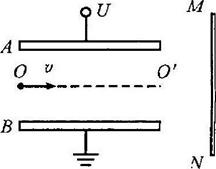
D
A.若它们射入电场时的初速度相同，在荧光屏上将只出现$${{1}}$$个亮点
B.若它们射入电场时的初动能相同，在荧光屏上将出现$${{2}}$$个亮点
C.若它们射入电场时的初动量相同，在荧光屏上将只出现$${{1}}$$个亮点
D.若它们的初速度是经同一加速电场从静止加速后获得的，则打在荧光屏上时，$$v_{\pi\in\mp} : v_{\pi\oplus\nnparallel}=\sqrt{2} : 1$$
7、['带电体（计重力）在电场中的运动'， '带电粒子在电场中的直线运动'， '带电粒子在电场中的曲线运动']正确率40.0%
如图所示，一价氢离子和二价氦离子的混合体 $${{(}}$$ 不计重力 $${{)}}$$ 经同一加速电场加速后，垂直射入同一偏转电场中，偏转后，打在同一荧光屏上，则它们 $${{(}{)}}$$
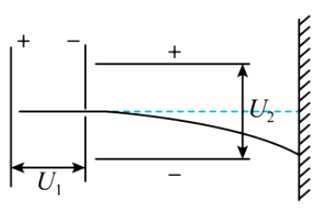
A.同时到达屏上同一点
B.先后到达屏上同一点
C.同时到达屏上不同点
D.先后到达屏上不同点
8、['示波管原理及其应用'， '带电粒子在电场中的直线运动'， '带电粒子在电场中的曲线运动']正确率40.0%下图是示波管的工作原理图。电子经电场加速后垂直于偏转电场方向射入偏转电场，若加速电压为$${{U}_{1}}$$，偏转电压为$${{U}_{2}}$$，偏转电场的极板长度与极板间的距离分别为$${{L}}$$和$${{d}{，}{y}}$$为电子离开偏转电场时发生的偏转距离。取$${{“}}$$单位偏转电压引起的偏转距离$${{”}}$$来描述示波管的灵敏度，即$$\frac y {U_{2}}，$$该比值越大则灵敏度越高，则下列哪种方法可以提高示波管的灵敏度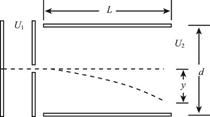
D
A.增大$${{U}_{1}}$$
B.增大$${{U}_{2}}$$
C.减小$${{L}}$$
D.减小$${{d}}$$
9、['静电力做功与电势差的关系'， '带电粒子在电场中的直线运动']正确率19.999999999999996%已知电场的方向平行于$${{x}}$$轴，其电场强度$${{E}}$$随坐标$${{x}}$$变化的图象如图所示(规定场强方向沿$${{x}}$$轴正方向为正$${{)}}$$。现把一个电荷量为$$q=-1. 6 \times1 0^{-2} C$$，质量为$$m=1. 6 \times1 0^{-1 2} \， k g$$的粒子在$${{x}{=}{{1}{0}}{m}}$$处由静止释放，忽略重力及一切阻力作用，下列说法正确的是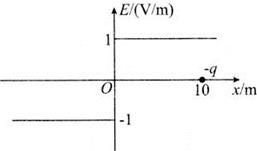
C
A.粒子做匀变速运动
B.粒子运动的周期为$$4 \sqrt{5} \times1 0^{-5} \mathrm{s}$$
C.粒子的最大速度为$$2 \sqrt{5} \times1 0^{5} \， \mathrm{m / s}$$
D.粒子从$${{x}{=}{{1}{0}}{m}}$$运动到$$x=-5 m$$的过程中电场力做功为$$0. 2 4 J$$
10、['带电粒子在交变电场中的运动'， '静电力做功与电势能的关系'， '带电粒子在电场中的直线运动'， '等量的同种电荷电场'， '电场强度的叠加']正确率19.999999999999996%如图甲所示，在场强大小为$${{E}_{0}}$$，方向水平向左$${的}$$匀强电场中，固定着一根光滑绝缘杆$${{O}{C}}$$和两个等量同种正点电荷$${{A}{、}{B}}$$，四边形$${{O}{A}{C}{B}}$$恰好构成菱形。一质量为$${{m}}$$、电荷量为$$- q ( q > 0 )$$的小球（可视为点电荷）套在绝缘杆上。令$${{x}}$$轴与$${{O}{C}}$$杆重合，以左端$${{O}}$$为坐标原点，以水平向左为两个正点电荷在$${{O}{C}}$$杆上产生的合场强的正方向，则该合场强在$${{O}{C}}$$杆上的变化规律如图乙所示，$${{E}_{m}}$$为该合场强的最大值。将小球从杆的左端$${{O}}$$由静止释放，小球沿杆运动过程中，下列说法正确的是（）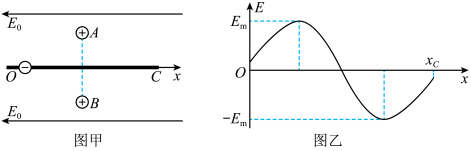
B
A.小球运动到$${{C}}$$点时的速度可能为$${{0}}$$
B.当$${{E}_{0}{>}{{E}_{m}}}$$时，小球电势能逐渐减小
C.当$${{E}_{0}{<}{{E}_{m}}}$$时，小球加速度先增大后减小
D.若移走$${{B}}$$电荷，仍从$${{O}}$$点由静止释放小球，则小球加速度最大值为$$\frac{q \left( 2 E_{0}+E_{\mathrm{m}} \right)} {2 m}$$
1. **解析**：
质子通过圆筒间隙时被电场加速，但在圆筒内部电场为零，质子做匀速运动，故A错误。质子进入第$$n$$个圆筒时已经经过$$n-1$$次加速，每次加速获得能量$$eU_0$$，由动能定理得$$\frac{1}{2}mv_n^2 = (n-1)eU_0$$，解得$$v_n = \sqrt{\frac{2(n-1)eU_0}{m}}$$，故B正确。圆筒长度需保证质子通过时电场极性恰好切换，即$$L_n = v_n \cdot \frac{T}{2}$$，其中$$T$$为交变电压周期。由于$$v_n \propto \sqrt{n-1}$$，圆筒长度之比为$$1 : \sqrt{2} : \sqrt{3} : \dots$$，故C正确。质子在每个圆筒中运动时间均为$$\frac{T}{2}$$，故D错误。
**答案**：B、C
2. **解析**：
粒子在电场中加速获得动能$$qU$$，与小车碰撞时动量守恒。设粒子穿出时速度为$$v$$，小车速度为$$V$$，由动量守恒和能量守恒得$$mv = MV$$和$$\frac{1}{2}mv^2 + \frac{1}{2}MV^2 = qU$$，解得$$v = \sqrt{\frac{2MqU}{m(M+m)}}$$，故C正确。小车最终会因粒子不断穿出而减速，故B错误。
**答案**：C
3. **解析**：
高频交变电压周期应与粒子回旋周期一致，即$$T = \frac{2\pi m}{Bq}$$，故A错误。粒子最大动能由$$R$$决定，$$E_k = \frac{(BqR)^2}{2m}$$，故B错误。第$$n$$次加速后速度$$v_n = \sqrt{\frac{2nqU}{m}}$$，半径$$r_n = \frac{mv_n}{Bq}$$，故第1次与第$$n$$次半径之比为$$1 : \sqrt{n}$$，C错误。粒子总时间$$t = \frac{E_k}{qU} \cdot \frac{T}{2} = \frac{BR^2}{2U}$$，故D正确。
**答案**：D
4. **解析**：
质子和电子电荷量相等、极性相反，电场力做功$$W = qEd$$相同，由动能定理得$$E_k = qU$$，故动能相同，C正确。加速度$$a = \frac{qE}{m}$$和质量相关，速率$$v = \sqrt{\frac{2qU}{m}}$$和质量相关，电势能变化量相同但符号相反，故A、B、D错误。
**答案**：C
5. **解析**：
粒子在复合场中需满足$$qE = qvB$$，即$$v = \frac{E}{B}$$。若换成$$^{2}_{1}H$$或$$^{1}_{1}H$$，其速度可能不满足$$v = \frac{E}{B}$$，故A、B正确。增大电压会改变粒子进入复合场的速度，可能破坏平衡条件，故D错误。
**答案**：A、B
6. **解析**：
若初速度相同，质子与氘核偏转距离不同，屏上出现两个亮点，A错误。若初动能相同，两者偏转距离相同，屏上出现一个亮点，B错误。若初动量相同，由$$y = \frac{qEL^2}{2mv_0^2}$$和$$mv_0$$相同，$$y$$相同，屏上出现一个亮点，C正确。若初速度由同一电场加速获得，$$v = \sqrt{\frac{2qU}{m}}$$，故$$v_{\text{质子}} : v_{\text{氘核}} = \sqrt{2} : 1$$，D正确。
**答案**：C、D
7. **解析**：
一价氢离子和二价氦离子经同一加速电场后速度不同，但在偏转电场中偏转距离$$y = \frac{qEL^2}{2mv_0^2}$$和飞行时间$$t = \frac{L}{v_0}$$均与$$q/m$$相关。由于两者$$q/m$$相同，偏转和飞行时间相同，故同时到达屏上同一点。
**答案**：A
8. **解析**：
灵敏度$$\frac{y}{U_2} = \frac{L^2}{4dU_1}$$，增大$$U_1$$会降低灵敏度，A错误。减小$$d$$可提高灵敏度，D正确。$$U_2$$和$$L$$的变化不影响比值，B、C错误。
**答案**：D
9. **解析**：
电场强度$$E$$随$$x$$变化，粒子做非匀变速运动，A错误。粒子在$$x=10\,m$$到$$x=-5\,m$$间周期性运动，由能量守恒和运动学分析可得周期$$T = 4\sqrt{5} \times 10^{-5}\,s$$，最大速度$$v_{\text{max}} = 2\sqrt{5} \times 10^5\,m/s$$，B、C正确。电场力做功$$W = q \int E \, dx = 0.24\,J$$，D正确。
**答案**：B、C、D
10. **解析**：
若$$E_0 > E_m$$，合场强始终向左，小球电势能减小，B正确。若$$E_0 < E_m$$，合场强先向左后向右，加速度先增后减，C正确。移走$$B$$后，最大合场强为$$E_0 + \frac{E_m}{2}$$，加速度最大值为$$\frac{q(2E_0 + E_m)}{2m}$$，D正确。小球到$$C$$点时速度可能为零（若$$E_0$$足够大），A正确。
**答案**：A、B、C、D