.jpg)
正确率40.0%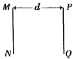
空间某区域内有场强为$${{E}}$$
A
A.$${\frac{1} {4}} q E d$$
B.$${\frac{1} {2}} q E d$$
C.$${{q}{E}{d}}$$
D.$${{2}{q}{E}{d}}$$
2、['静电力做功与电势能的关系'， '其他抛体运动'， '带电粒子在电场中的曲线运动']正确率40.0%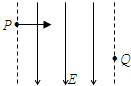
如图所示，在两条竖直边界线所围的匀强电场中，一个不计重力的带电粒子从左边界的$${{P}}$$
D
A.粒子带负电
B.粒子做匀速圆周运动
C.粒子电势能增大
D.仅增大电场强度粒子通过电场的时间不变
3、['静电力做功与电势能的关系'， '物体运动轨迹、速度、受力的相互判断'， '带电粒子在电场中的曲线运动'， '动能定理的简单应用']正确率40.0%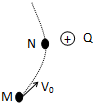
如图所示，在正点电荷形成的电场中，一个带电体运动轨迹如图虚线所示，不计重力，它经过$${{M}{，}{N}}$$
C
A.$$E_{A} > E_{B}， \， \， E_{K M} < E_{K N}$$
B.$$E_{A} < E_{B}， \， \， E_{K M} < E_{K N}$$
C.$$E_{A} < E_{B}， \， \， E_{K M} > E_{K N}$$
D.$$E_{A} > E_{B}， \， \， E_{K M} > E_{K N}$$
4、['匀强电场中电势差与电场强度的关系'， '平抛运动基本规律及推论的应用'， '静电力做功与电势能的关系'， '带电粒子在电场中的曲线运动']正确率40.0%如图所示，竖直平面内有水平向左的匀强电场$${{E}{，}{M}}$$点与$${{N}}$$点在同一电场线上。两个质量相等的带正电荷的粒子，以相同的速度$${{v}_{0}}$$分别从$${{M}}$$点和$${{N}}$$点同时垂直进入电场，重力不计。两粒子都能经过$${{P}}$$点，在此过程中，下列说法正确的是（）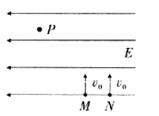
D
A.从$${{N}}$$点进入的粒子先到达$${{P}}$$点
B.从$${{M}}$$点进人的粒子先到达$${{P}}$$点
C.两粒子到达$${{P}}$$点时的电势能都增加
D.从$${{M}}$$点进入的粒子的电量小于从$${{N}}$$点进入的粒子的电量
5、['其他抛体运动'， '竖直平面内的圆周运动'， '带电粒子在电场中的曲线运动'， '带电粒子在有界磁场中的运动']正确率40.0%如图，足够长的水平虚线$${{M}{N}}$$上方有一匀强电场，方向竖直向下(与纸面平行$${{)}}$$；下方有一匀强磁场，方向垂直纸面向里。一个带电粒子从电场中的$${{A}}$$点以水平初速度$${{v}_{0}}$$向右运动，第一次穿过$${{M}{N}}$$时的位置记为$${{P}}$$点，第二次穿过$${{M}{N}}$$时的位置记为$${{Q}}$$点，$${{P}{Q}}$$两点间的距离记为$${{d}}$$，从$${{P}}$$点运动到$${{Q}}$$点的时间记为$${{t}}$$。不计粒子的重力，若增大$${{v}_{0}}$$，则$${{(}{)}}$$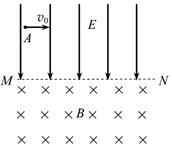
D
A.$${{t}}$$不变，$${{d}}$$不变
B.$${{t}}$$不变，$${{d}}$$变小
C.$${{t}}$$变小，$${{d}}$$变小
D.$${{t}}$$变小，$${{d}}$$不变
6、['静电力做功与电势差的关系'， '匀变速直线运动的位移与时间的关系'， '匀变速直线运动的速度与时间的关系'， '运动的合成、分解'， '带电粒子在电场中的曲线运动']正确率19.999999999999996%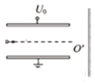
真空中的某装置如图所示，现有质子$$( \frac{1} {1} H )$$
C
A.三种粒子以相同的初速度进入偏转场射出时电场力做功之比为$$1 : ~ 1 : ~ 4$$
B.三种粒子以相同的动能进入偏转场，射出时速度偏转角的正切值之比为$$1_{:} ~ 2_{:} ~ 4$$
C.三种粒子出以相同的动量进入偏转场，屏上有$${{3}}$$个亮点
D.三种粒子经过同一个加速场后进入偏转场，屏上有$${{2}}$$个亮点
7、['静电力做功'， '带电粒子在电场中的曲线运动']正确率40.0%水平放置的平行金属板$${{A}}$$、$${{B}}$$连接一恒定电压，两个质量相等的电荷$${{M}}$$和$${{N}}$$同时分别从极板$${{A}}$$的边缘和两极板的正中间沿水平方向进入板间电场，两电荷恰好在板间某点相遇，如图所示.若不考虑电荷的重力和它们之间的相互作用，则下列说法正确的是（）
A
A.电荷$${{M}}$$的比荷大于电荷$${{N}}$$的比荷
B.两电荷在电场中运动的加速度相等
C.从两电荷进入电场到两电荷相遇，静电力对电荷$${{M}}$$做的功等于静电力对电荷$${{N}}$$做的功
D.电荷$${{M}}$$进入电场的初速度大小与电荷$${{N}}$$进入电场的初速度大小一定相同
8、['带电粒子在电场中的曲线运动']正确率60.0%让质子$$( \frac{1} {1} H )$$氘核$$\langle{\;_{1}^{2} H} \rangle$$和氦核
的混合物以相同的速度垂直电场方向进入同一偏转电场，则它们离开电场时（）
B
A.仍是一股离子束
B.会分离为两股离子束
C.会分离为三股粒子束
D.无法确定
9、['带电粒子在复合场中的运动'， '带电粒子在电场中的曲线运动'， '带电粒子在有界磁场中的运动']正确率60.0%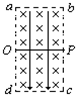
如图所示，在长为宽$${{2}}$$
A
A.$${{O}{、}{a}}$$之间
B.$${{a}{、}{b}}$$之间
C.$${{b}}$$点
D.$${{P}{、}{b}}$$之间
10、['带电粒子在电场中的曲线运动'， '电场线的概念及特点']正确率40.0%如图所示，电场某区域的电场线分布，一带正电的点电荷在$${{P}}$$点由静止开始运动，在只有电场力作用下，它的运动轨迹（图中用粗黑线表示）应该是（）
C
A.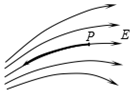
B.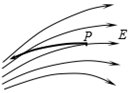
C.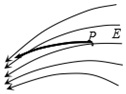
D.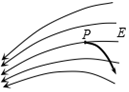
1. 题目未给出完整信息，无法解析。通常电场力做功公式为 $$W = qEd$$，但选项中的分数关系需要具体情境支持。
2. 粒子从左边界的 $$P$$ 点进入匀强电场，若不计重力，其运动由电场力决定：
- 若粒子带负电，电场力方向与场强方向相反，可能向左偏转，但需具体轨迹判断。
- 匀速圆周运动需向心力，而电场力为恒力，不满足条件（B错误）。
- 若电场力做负功，电势能增大（C可能正确）。
- 仅增大电场强度，粒子加速度增大，但水平速度不变时，通过时间可能不变（D可能正确）。
3. 正点电荷电场中，带电体轨迹为曲线：
- $$M$$ 点比 $$N$$ 点更靠近场源电荷，故 $$E_A > E_B$$。
- 若带电体受斥力，从 $$M$$ 到 $$N$$ 电场力做正功，动能 $$E_{KM} < E_{KN}$$（A正确）。
4. 两粒子质量相等，初速度相同，均能到达 $$P$$ 点：
- 从 $$N$$ 点进入的粒子水平位移更小，时间更短（A正确）。
- 电场力对两粒子均做正功，电势能应减小（C错误）。
- 从 $$M$$ 点进入的粒子需更大偏转，故电量可能更大（D错误）。
5. 粒子在电场中做类平抛运动，在磁场中做匀速圆周运动：
- 增大 $$v_0$$ 会缩短电场中运动时间，但磁场中周期 $$T = \frac{2\pi m}{qB}$$ 与速度无关，$$t$$ 不变。
- $$d$$ 为两倍回旋半径 $$r = \frac{mv}{qB}$$，$$v$$ 增大时 $$d$$ 增大，但题目描述矛盾，需重新审题。
6. 质子、氘核、氦核的电荷数比为 $$1:1:2$$，质量数比为 $$1:2:4$$：
- 电场力做功 $$W = qU$$，与电荷量成正比，比为 $$1:1:2$$（A错误）。
- 速度偏转角正切值 $$\tan \theta = \frac{qEL}{mv_0^2}$$，动能相同时比为 $$1:2:4$$（B正确）。
- 相同动量时，偏转量与 $$q/m$$ 有关，三种粒子 $$q/m$$ 不同，屏上出现 $$3$$ 个亮点（C正确）。
- 经过同一加速场后，动能相同，由B项分析知屏上 $$2$$ 个亮点（氘核与质子重合，D正确）。
7. 电荷 $$M$$ 和 $$N$$ 在电场中相遇：
- $$M$$ 的侧向位移更大，加速度更大，故比荷更大（A正确）。
- 静电力做功 $$W = qEy$$，$$M$$ 的 $$q$$ 和 $$y$$ 均可能更大，无法确定功是否相等（C错误）。
- 初速度关系需具体计算，不一定相同（D错误）。
8. 质子、氘核、氦核的 $$q/m$$ 比为 $$1:0.5:0.5$$：
- 偏转量取决于 $$q/m$$，氘核与氦核 $$q/m$$ 相同，故分离为两股离子束（B正确）。
9. 题目信息不完整，无法解析。
10. 正电荷受力沿电场线切线方向，轨迹应逐渐远离场源：
- 选项需满足曲线切线方向与场强方向一致，且向电势降低处运动。
- 图中B选项符合电场线分布规律。