.jpg)
正确率80.0%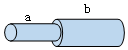
如图所示，两段长度和材料相同、各自粗细均匀的金属导线$${{a}}$$、$${{b}}$$，单位体积内的自由电子数相等，横截面积之比$${{S}_{a}}$$：$${{S}_{b}{=}{1}}$$：$${{2}{.}}$$已知$${{5}{s}}$$内有$$5 \times1 0^{1 8}$$个自由电子通过导线$${{a}}$$的横截面，电子的电荷量$$e=1. 6 \times1 0^{-1 9} \， C.$$下列说法正确的是$${{(}{)}}$$
A.流经导线$${{a}}$$的电流为$$0. 1 6 A$$
B.流经导线$${{b}}$$的电流为$$0. 3 2 A$$
C.$${{a}}$$、$${{b}}$$的电阻之比$${{R}_{a}}$$：$${{R}_{b}{=}{1}}$$：$${{2}}$$
D.自由电子在导线$${{a}}$$和$${{b}}$$中的定向移动速率之比$${{v}_{a}}$$：$${{v}_{b}{=}{1}}$$：$${{2}}$$
2、['电阻定律']正确率40.0%地球表面附近存在一个竖直向下的电场，晴天时在电场作用下，大气中的正离子向下运动、负离子向上运动，如此形成的微弱电流称地空电流。该电流比较稳定，不随高度变化，全球地空电流的总电流强度为$${{I}}$$。假设地空电流在全球各处均匀分布，地球附近竖直向下的电场场强为$${{E}}$$，取地球表面积为$${{S}}$$，地表附近空气的电阻率$${{ρ}_{0}}$$的大小为$${{(}{)}}$$
A
A.$$\frac{E S} {I}$$
B.$$\frac{E^{2} S} {I}$$
C.$$\frac{S^{2} E} {I}$$
D.$$\frac{E S} {I^{2}}$$
3、['电阻定律'， '欧姆定律适用条件及其计算']正确率80.0% 如图所示，厚薄均匀的矩形金属薄片边长为 $${{a}{b}}$$ $${{=}{{3}{0}}{c}{m}}$$ ， $${{b}{c}}$$ $${{=}{{1}{0}}{c}{m}}$$ ，当将 $${{C}}$$ 与 $${{D}}$$ 接入电压恒为 $${{U}}$$ 的电路时，电流为 $${{I}}$$ ，若将 $${{A}}$$ 与 $${{B}}$$ 接入电路中时电流仍为 $${{I}}$$ ，则接入的电压为 $${{(}{)}}$$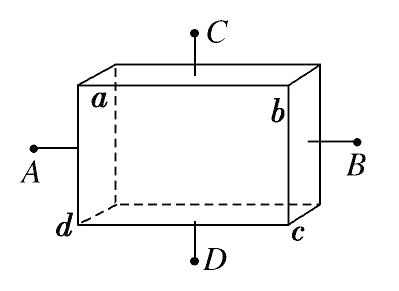
A. $${{U}}$$
B. $${{1}{.}{5}}$$ $${{U}}$$
C. $${{3}}$$ $${{U}}$$
D. $${{9}}$$ $${{U}}$$
4、['电阻定律']正确率60.0%两根材料和质量均相同的电阻丝$${{R}_{1}{、}{{R}_{2}}}$$，它们的长度之比$${{l}_{1}{、}{{l}_{2}}}$$为$${{4}{：}{3}}$$，则（）
C
A.$$R_{1} \colon~ R_{2}=4 \colon~ 3$$
B.$$R_{1} \colon~ R_{2}=3 \colon~ 4$$
C.$$R_{1} \colon~ R_{2}=1 6 \colon~ 9$$
D.$$R_{1} \colon~ R_{2}=9 \colon~ 1 6$$
5、['电阻定律']正确率60.0%根据电阻定律，电阻率，对于某种金属导线来说，它的电阻率（）
B
A.跟导线的电阻和横截面积成正比
B.由所用金属材料本身决定
C.跟导线的长度成反比
D.随温度的升高而减小
6、['电阻定律']正确率60.0%两根同种材料的电阻丝，长度之比为$${{1}{：}{5}}$$，横截面积之比为$${{2}{：}{3}}$$，则它们的电阻值之比为（）
D
A.$${{1}{：}{5}}$$
B.$${{2}{：}{3}}$$
C.$${{3}{：}{2}}$$
D.$${{3}{：}{{1}{0}}}$$
7、['电流的微观表达式及其应用'， '电阻定律'， '欧姆定律适用条件及其计算'， '串、并联电路的规律']正确率40.0%同样粗细等长的铜棒和铁棒接在一起后接人电路，如图所示，已知铜的电阻率比铁的电阻率小，则下列说法正确的是
A
A.铜棒两端电压小于铁棒两端电压
B.两棒内电子定向移动的速率相等
C.两棒内电场强度相等
D.通过两棒的电流强度不等
8、['电阻定律'， '闭合电路欧姆定律内容、表达式、及其能量分析']正确率40.0%一根粗细均匀的导线，两端加上电压$${{U}}$$时，通过导线中的电流强度为$${{I}}$$；若导线均匀拉长，使其半径变为原来的$$\frac{1} {2}，$$再给它两端加上电压$${{U}}$$，则通过导线的电流为$${{(}{)}}$$
A
A.$$\frac{I} {1 6}$$
B.$$\begin{array} {c} {\frac{I} {8}} \\ \end{array}$$
C.$$\frac{I} {4}$$
D.$$\frac{I} {2}$$
9、['电阻定律'， '欧姆定律适用条件及其计算']正确率80.0%两根材料相同的导线，长度之比为$${{1}{∶}{2}}$$，横截面积之比为$${{4}{∶}{1}}$$，两端加上相同的电压后，通过的电流之比为$${{(}{)}}$$
C
A.$${{2}{∶}{1}}$$
B.$${{1}{∶}{2}}$$
C.$${{8}{∶}{1}}$$
D.$${{1}{∶}{8}}$$
10、['电阻定律']正确率80.0%一根粗细均匀，阻值为$${{8}{Ω}}$$的电阻丝，在温度不变的情况下，先将它等分成$${{2}}$$段，每段电阻为$${{R}_{1}}$$；再将这$${{2}}$$段电阻丝并联，并联后总电阻为$${{R}_{2}}$$.则$${{R}_{1}}$$与$${{R}_{2}}$$的大小依次为（）
B
A.$$1 \Omega， ~ 0. 5 \Omega$$
B.$$4 \Omega， ~ 2 \Omega$$
C.$$2 \Omega， ~ 0. 5 \Omega$$
D.$$4 \Omega， ~ 1 \Omega$$
1. 解析：
首先计算流经导线 $$a$$ 的电流。已知 $$5s$$ 内有 $$5 \times 10^{18}$$ 个电子通过，电子电荷量 $$e = 1.6 \times 10^{-19} C$$，则电流 $$I_a = \frac{Q}{t} = \frac{5 \times 10^{18} \times 1.6 \times 10^{-19}}{5} = 0.16 A$$，选项 A 正确。
由于导线 $$a$$ 和 $$b$$ 串联，电流相同，故 $$I_b = I_a = 0.16 A$$，选项 B 错误。
电阻公式为 $$R = \rho \frac{L}{S}$$，由于材料相同、长度相同，电阻与横截面积成反比，故 $$R_a : R_b = S_b : S_a = 2 : 1$$，选项 C 错误。
电流微观表达式为 $$I = n e S v$$，由于 $$I$$、$$n$$、$$e$$ 相同，故 $$v_a : v_b = S_b : S_a = 2 : 1$$，选项 D 错误。
2. 解析：
地空电流均匀分布，电流密度 $$J = \frac{I}{S}$$。根据欧姆定律微分形式 $$J = \frac{E}{\rho_0}$$，解得 $$\rho_0 = \frac{E}{J} = \frac{E S}{I}$$，选项 A 正确。
3. 解析：
设金属薄片厚度为 $$d$$，电阻率为 $$\rho$$。当 $$C$$ 与 $$D$$ 接入时，长度 $$L_1 = 10 cm$$，横截面积 $$S_1 = 30d$$，电阻 $$R_1 = \rho \frac{L_1}{S_1} = \rho \frac{10}{30d}$$。
当 $$A$$ 与 $$B$$ 接入时，长度 $$L_2 = 30 cm$$，横截面积 $$S_2 = 10d$$，电阻 $$R_2 = \rho \frac{L_2}{S_2} = \rho \frac{30}{10d}$$。
由题意电流相同，故电压比等于电阻比，即 $$\frac{U'}{U} = \frac{R_2}{R_1} = \frac{9}{1}$$，因此 $$U' = 9U$$，选项 D 正确。
4. 解析：
材料和质量相同，则体积相同，故横截面积之比 $$S_1 : S_2 = l_2 : l_1 = 3 : 4$$。电阻公式 $$R = \rho \frac{L}{S}$$，故 $$R_1 : R_2 = \frac{l_1}{S_1} : \frac{l_2}{S_2} = \frac{4}{3} : \frac{3}{4} = 16 : 9$$，选项 C 正确。
5. 解析：
电阻率是材料的固有属性，由金属材料本身决定，与导线的几何尺寸无关，选项 B 正确。电阻率通常随温度升高而增大，选项 D 错误。
6. 解析：
电阻公式 $$R = \rho \frac{L}{S}$$，同种材料电阻率相同，故电阻之比为 $$\frac{1}{2} : \frac{5}{3} = 3 : 10$$，选项 D 正确。
7. 解析：
铜棒和铁棒串联，电流相同，选项 D 错误。由于铜的电阻率小，电阻小，根据 $$U = IR$$，铜棒两端电压小，选项 A 正确。电场强度 $$E = \frac{U}{L}$$，铜棒电场强度小，选项 C 错误。电子定向移动速率与材料有关，不相等，选项 B 错误。
8. 解析：
导线拉长后半径变为 $$\frac{1}{2}$$，横截面积变为 $$\frac{1}{4}$$，长度变为 $$4$$ 倍。电阻公式 $$R = \rho \frac{L}{S}$$，故电阻变为 $$16$$ 倍。电流 $$I = \frac{U}{R}$$，变为 $$\frac{1}{16}$$ 倍，选项 A 正确。
9. 解析：
电阻之比为 $$\frac{1}{4} : \frac{2}{1} = 1 : 8$$，电压相同，电流之比为电阻的反比，即 $$8 : 1$$，选项 C 正确。
10. 解析：
原电阻丝 $$8 \Omega$$ 等分成 $$2$$ 段，每段 $$R_1 = 4 \Omega$$。并联后 $$R_2 = \frac{4}{2} = 2 \Omega$$，选项 B 正确。