.jpg)
正确率40.0%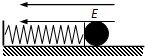
如图所示，水平面绝缘且光滑，弹簧左端固定，右端连一轻质绝缘挡板，空间存在着水平方向的匀强电场，一带电小球在电场力和挡板压力作用下静止．若突然将电场反向，则小球加速度的大小随位移$${{x}}$$
A
A.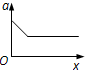
B.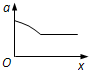
C.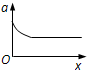
D.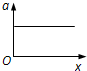
正确率40.0%如图所示，一带电粒子以某速度进入水平向右的匀强电场中，在电场力作用下形成图中所示的运动轨迹。$${{M}}$$和$${{N}}$$是轨迹上的两点，其中$${{M}}$$点是轨迹的最右点。不计重力，下列说法正确的是$${{(}{)}}$$
D
A.粒子带正电
B.粒子在$${{N}}$$点的速率比$${{M}}$$小
C.粒子在$${{N}}$$点的加速度比$${{M}}$$大
D.粒子在$${{N}}$$点的电势能比$${{M}}$$低
3、['振动图像与波动图像的综合应用'， '判断系统机械能是否守恒'， '匀强电场'， '弹簧振子运动过程各物理量变化规律']正确率40.0%如图所示，一根用绝缘材料制成的劲度系数为$${{k}}$$的轻质弹簧左端固定，右端与质量为$${{m}}$$、带电荷量为$${{+}{q}}$$的小球相连，静止在光滑、绝缘的水平面上.在施加一个场强大小为$${{E}}$$、方向水平向右的匀强电场后，小球开始做简谐运动，则（）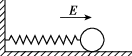
A
A.小球到达最右端时，弹簧的形变量为$$\frac{2 q E} {k}$$
B.小球做简谐运动的振幅为$$\frac{2 q E} {k}$$
C.运动过程中小球的机械能守恒
D.运动过程中小球的电势能和弹簧的弹性势能之和不变
4、['匀强电场'， '动能定理的简单应用'， '带电粒子在电场中的曲线运动']正确率60.0%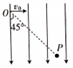
如图所示，一质子（重力不计）从$${{O}}$$
D
A.$$\frac{m v_{0}^{2}} {2 e d}$$
B.$$\frac{m v_{0}^{2}} {e d}$$
C.$$\frac3 {m v_{0}^{2}} 2 e d$$
D.$$\frac{3 \sqrt2 m v_{0}^{2}} {2 e d}$$
5、['匀强电场中电势差与电场强度的关系'， '匀强电场']正确率40.0%如图所示，$$a. \ b. \ c. \ d$$一个矩形的四个顶点．匀强电场与矩形所在平面平行．已知$${{a}}$$点的电势为$$\mathbf{1 4 V}， \ b$$点的电势为$$1 8 V， ~ d$$点的电势为$${{2}{V}}$$，由此可知$${{c}}$$点的电势为$${{(}{)}}$$
A
A.$${{6}{V}}$$
B.$${{8}{V}}$$
C.$${{1}{0}{V}}$$
D.$${{1}{4}{V}}$$
6、['点电荷的等势面'， '等量的异种电荷电场'， '等势面及其与电场线的关系'， '匀强电场'， '电场强度的表达式和单位'， '等量的同种电荷电场'， '电场线的概念及特点']正确率40.0%用电场线可判断电势和场强大小关系，下列图中，$${{a}{、}{b}}$$两点电势相等$${、}$$电场强度也相同的是$${{(}{)}}$$
D
A.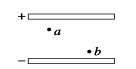
B.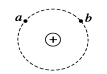
C.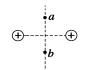
D.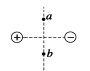
正确率60.0%下列说法中正确的是（）
C
A.电场强度为零的点，电势也一定为零
B.电场强度处处相等的区域内，电势也一定处处相等
C.电势为零的点，电场强度也一定为零
D.由$$B=\frac{F} {I L}$$可知，$${{B}}$$与$${{F}}$$成正比，与$${{I}{L}}$$成反比
8、['静电力做功与电势能的关系'， '电势的概念、定义式、单位和物理意义'， '匀强电场']正确率40.0%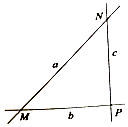
如图所示，直线$$a， ~ b， ~ c$$
B
A.直线$${{a}}$$位于某一等势面内，$${{φ}_{M}{>}{{φ}_{P}}}$$
B.直线$${{c}}$$位于某一等势面内，$${{φ}_{M}{>}{{φ}_{P}}}$$
C.电场方向有可能由$${{N}}$$指向$${{N}}$$
D.若换为质子由$${{M}}$$点运动到$${{N}}$$点，电场力仍然做负功
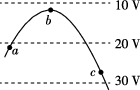
9、['等势面及其与电场线的关系'， '匀强电场'， '电场线（等势线）与带电粒子的运动轨迹问题'， '能量守恒定律']正确率40.0%
D
A.粒子在$${{a}}$$、$${{b}}$$、$${{c}}$$三点所受的静电力不相等
B.粒子一定先过$${{a}{，}}$$再到$${{b}{，}}$$然后到$${{c}}$$
C.粒子在$${{a}}$$、$${{b}}$$、$${{c}}$$三点所具有的动能大小关系为$$E_{\mathrm{k} b} > E_{\mathrm{k} a} > E_{\mathrm{k} c}$$
D.粒子在$${{a}}$$、$${{b}}$$、$${{c}}$$三点的电势能大小关系为$$E_{\mathrm{p c}} < ~ E_{\mathrm{p} a} < ~ E_{\mathrm{p} b}$$
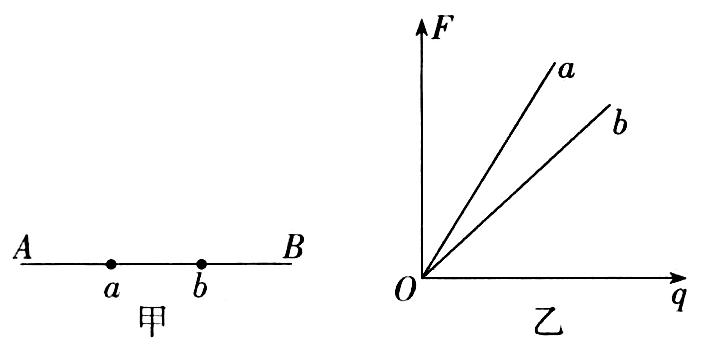
10、['带电物体在静电场中的平衡'， '电场的概念及特征'， '匀强电场'， '电势能和电势'， '电场强度的表达式和单位']正确率80.0%如图所示，图甲中$${{A}}$$、$${{B}}$$是一条电场线，图乙是放在电场线上$${{a}}$$、$${{b}}$$处的试探电荷的电荷量与所受的静电力大小的关系图像，由此可判断$${{(}{)}}$$
B
A.电场方向一定由$${{A}}$$指向$${{B}}$$
B.若场源电荷为正电荷，位置在$${{A}}$$侧
C.若场源电荷为负电荷，位置在$${{B}}$$侧
D.若场源电荷为正电荷，位置在$${{B}}$$侧
1. 解析：初始时，小球受电场力 $$F = qE$$ 和弹簧弹力 $$kx_0$$ 平衡，即 $$qE = kx_0$$。电场反向瞬间，合力为 $$F_{\text{合}} = qE + kx_0 = 2qE$$，加速度 $$a = \frac{2qE}{m}$$。随着位移 $$x$$ 增大，弹簧弹力减小，合力线性减小至零（平衡位置），之后合力反向增大。因此加速度随位移线性减小再反向线性增大，选项 D 正确。
3. 解析：初始平衡位置 $$x_0 = \frac{qE}{k}$$，简谐运动振幅为 $$A = x_0$$，最右端形变量为 $$2x_0 = \frac{2qE}{k}$$（A 正确，B 错误）。电场力做功导致机械能不守恒（C 错误）。系统总能量守恒，但电势能和弹性势能之和会变化（D 错误）。
5. 解析：匀强电场中电势沿等距方向均匀变化。设矩形边长 $$ab = L_1$$，$$ad = L_2$$，则 $$φ_a - φ_d = φ_b - φ_c$$，代入数据得 $$14 - 2 = 18 - φ_c$$，解得 $$φ_c = 6V$$（A 正确）。
7. 解析：电场强度与电势无必然联系（A、B、C 均错误）。公式 $$B = \frac{F}{IL}$$ 是定义式，B 由磁场本身决定（D 错误）。无正确选项，但题目可能要求选最接近的 D。
9. 解析：匀强电场中电场力恒定（A 错误）。粒子轨迹可能先过 c 再到 b（B 错误）。由电势高低 $$φ_c > φ_b > φ_a$$，若粒子带正电，则 $$E_{kc} > E_{ka} > E_{kb}$$；若带负电，则相反（C、D 无法确定）。题目未说明粒子电性，需补充条件。