.jpg)
正确率40.0%如图所示，在$${{y}}$$轴上关于$${{0}}$$点对称的$${{A}{、}{B}}$$两点有等量同种点电荷$${{+}{Q}}$$，在$${{x}}$$轴上$${{C}}$$点有点电荷$${{−}{Q}}$$且$$C O=O D， \， \， \， \angle A D O=6 0^{0}$$。下列判断正确的是 $${{(}{)}}$$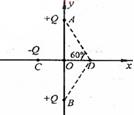 
B
A.$${{O}}$$点电场强度为零
B.$${{D}}$$点电场强度为零
C.若将点电荷$${{+}{q}}$$从$${{O}}$$移向$${{C}}$$，电势能增大
D.若将点电荷$${{−}{q}}$$从$${{O}}$$移向$${{C}}$$，电场力做正功
2、['动能定理和图像的综合问题'， '电场强度的叠加']正确率40.0%在$${{x}}$$轴上有两个固定的点电荷$${{Q}_{i}{、}{{Q}_{2}}}$$，其中$${{Q}_{1}}$$为正电荷，$${{Q}_{2}}$$为负电荷。一带正电的粒子仅在电场力作用下从原点$${{O}}$$由静止开始沿$${{x}}$$轴运动，其动能$${{E}_{k}}$$随位置$${{x}}$$的变化关系如图，则能够正确表示$${{Q}_{1}{、}{{Q}_{2}}}$$位置的图象是（）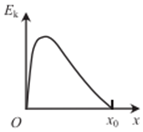
A
A.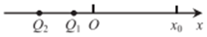
B.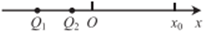
C.
D.
正确率60.0%如图所示$${，{A}}$$、$${{B}}$$、$${{C}}$$、$${{D}}$$、$${{E}}$$是半径为$${{r}}$$的圆周上等间距的五个点，在这些点上各固定一个点电荷，除$${{A}}$$点处点电荷的电荷量为$${{−}{q}}$$外，其余各点处点电荷的电荷量均为$${{+}{q}{，}}$$则圆心$${{O}}$$处$${{(}{k}}$$为静电力常量)（）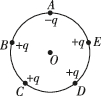
C
A.场强大小为$$\frac{3 k q} {r^{2}}，$$方向沿$${{O}{A}}$$方向
B.场强大小为$$\frac{3 k q} {r^{2}}，$$方向沿$${{A}{O}}$$方向
C.场强大小为$$\frac{2 k q} {r^{2}}，$$方向沿$${{O}{A}}$$方向
D.场强大小为$$\frac{2 k q} {r^{2}}，$$方向沿$${{A}{O}}$$方向
4、['电场强度的表达式和单位'， '点电荷的电场'， '电场强度的叠加']正确率60.0%一段均匀带电的半圆形细线在其圆心$${{O}}$$处产生的场强大小为$${{E}}$$，把细线分成等长的圆弧$$A B. ~ B C. ~ C D$$，则圆弧$${{B}{C}}$$在圆心$${{O}}$$处产生的场强大小为$${{(}{)}}$$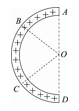
B
A.$${{E}}$$
B.$${{E}{/}{2}}$$;
C.$${{E}{/}{3}}$$;
D.$${{E}{/}{4}}$$;
5、['点电荷的等势面'， '点电荷的电场'， '电势高低与电势能大小的判断'， '电场强度的叠加']正确率40.0%如图所示，$$A C \backslash\ B D$$为圆的两条相互垂直的直径，圆心为$${{O}}$$，半径为$${{R}}$$，电荷量均为$${{Q}}$$的正负点电荷放在圆周上，它们的位置关于$${{A}{C}}$$对称，，已知$${{+}{Q}}$$与$${{O}}$$点的连线和$${{O}{C}}$$夹角为$${{6}{0}^{∘}}$$，下列说法正确的是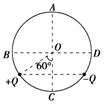
B
A.$${{O}}$$点电场强度大小为$$\frac{k Q} {R^{2}}，$$方向由$${{O}}$$指向$${{D}}$$
B.$${{O}}$$点电场强度大小为$$\frac{\sqrt{3} k Q} {R^{2}}，$$方向由$${{O}}$$指向$${{D}}$$
C.$${{A}{、}{C}}$$两点的电势关系是$${{φ}_{A}{<}{{φ}_{C}}}$$
D.$${{A}}$$电荷量为$${{q}}$$的正电荷在$${{A}}$$点的电势能大于在$${{C}}$$点的电势能
6、['点电荷的等势面'， '点电荷的电场'， '电场强度的叠加']正确率60.0%
如图所示的两个电场中，点电荷$${{+}{Q}}$$
A
A.$${{a}{、}{b}}$$两点场强不同，电势相同
B.$${{a}{、}{b}}$$两点场强不同，电势不同
C.$${{c}{、}{d}}$$两点场强相同，电势相同
D.$${{c}{、}{d}}$$两点场强相同，电势不同
7、['电场的概念及特征'， '电场强度的叠加']正确率60.0%$${{1}{9}}$$世纪$${{3}{0}}$$年代，法拉第提出一种观点，认为在电荷周围存在电场，电荷之间通过电场传递相互作用力.对于电荷$${{A}}$$和电荷$${{B}}$$之间的电场，下列说法中正确的是$${{(}{)}}$$
D
A.电荷$${{B}}$$在电荷$${{A}}$$的电场中受电场力的作用，自身并不产生电场
B.撤去电荷$${{B}}$$，电荷$${{A}}$$激发的电场就不存在了
C.电场是法拉第假想的，实际上并不存在
D.空间某点的电场强度等于两电荷在该点激发电场的场强的矢量和
8、['电势能的概念及相对性'， '静电力做功与电势差的关系'， '等量的同种电荷电场'， '点电荷的电场'， '电场强度的叠加']正确率40.0%如图所示，水平绝缘杆的两端分别固定着所带电荷量均为$${{+}{Q}}$$的点电荷。有一质量为$${{m}}$$，所带电荷量为$${{+}{q}}$$，且可看作点电荷的小球用长为$${{L}}$$的绝缘轻绳系于杆的中点$${{O}}$$。把小球拉至最高点，给其垂直纸面向里的水平速度$${{v}_{0}}$$，使小球绕$${{O}}$$点做曲线运动，直至轻绳全部绕在杆上。在小球运动过程中，下列各说法正确的是(重力加速度为$${{g}{)}{（}}$$）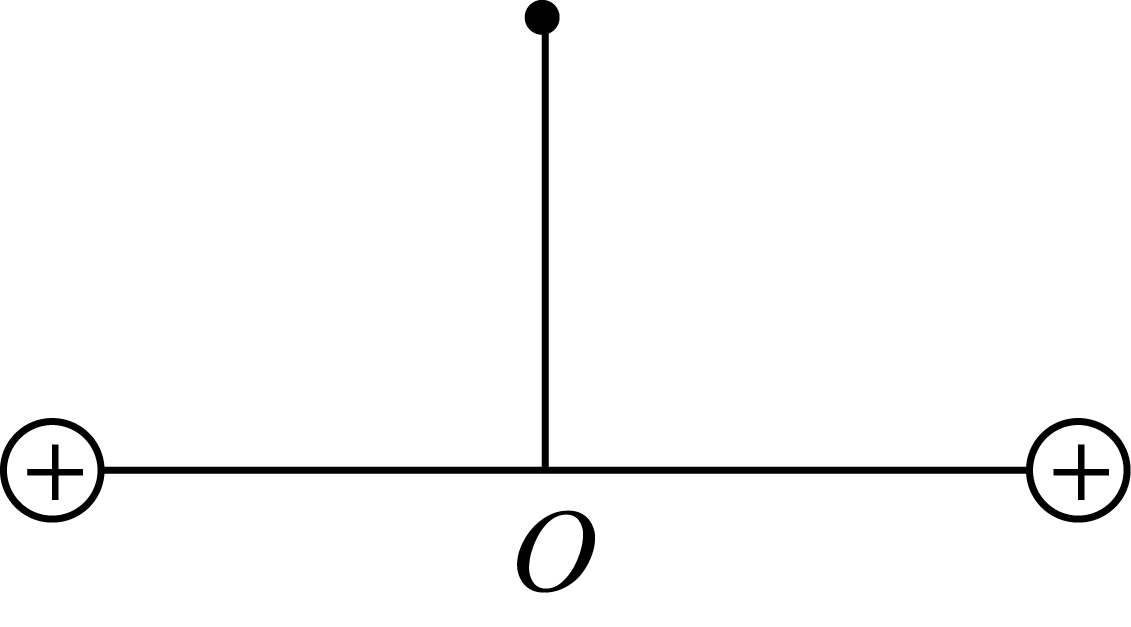
C
A.$${{O}}$$点的电场强度一直为零
B.水平速度$${{v}_{0}}$$的最小值为$${\sqrt {{g}{L}}}$$
C.小球所受的电场力可能逐渐减小
D.小球的电势能可能先增大后减小
9、['电势的计算'， '电场强度的叠加'， '对称法和挖补法']正确率19.999999999999996%已知半径为$${{R}{、}}$$电荷量为$${{q}}$$的均匀带电球面内的各点电势相等，其值为$$\varphi=k \frac{q} {R} \wedge k$$为静电力常量）．图为半径为$${{R}}$$的半球形薄壳，开口圆面水平，半球表面均匀分布单位面积带电量为$${{σ}}$$的正电荷，$${{O}}$$为球心，$${{P}}$$为开口处圆面上的任意一点，则$${{P}}$$点的场强方向和电势的大小分别为（已知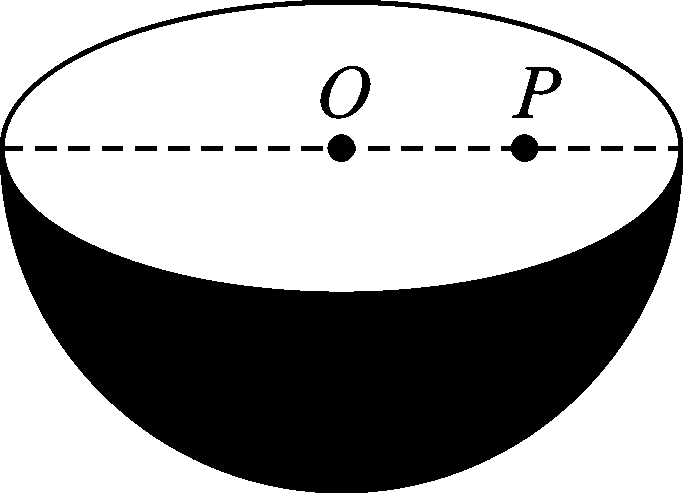
$${}$$半径为$${{R}}$$的球的表面积为$$4 \pi R^{2} \， ) \ ($$）
B
A.竖直向上，$${{0}}$$
B.竖直向上，$$2 \pi k \sigma R$$
C.竖直向下，$$2 \pi k \sigma R$$
D.竖直向下，$$4 \pi k \sigma R$$
10、['静电力做功与电势能的关系'， '点电荷的电场'， '电势高低与电势能大小的判断'， '电场强度的叠加']正确率40.0%如图所示，$${{△}{A}{B}{C}}$$与$${{△}{A}{B}{D}}$$为两个全等的直角三角形，$$\angle D B A=\angle C A B=3 0^{\circ}， \; \; E$$为$${{A}{C}}$$与$${{B}{D}}$$边的中点。在$${{A}{、}{B}}$$两点分别放置一个点电荷后，$${{C}}$$点的场强方向沿$${{C}{D}}$$方向指向$${{D}}$$，则（）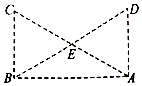
D
A.一定是$${{A}}$$点放正电荷，$${{B}}$$点放负电荷
B.电场中$${{C}{、}{D}}$$两点的场强相同
C.$${{C}{E}}$$两点间的电势差与$${{E}{D}}$$两点间的电势差相等
D.将一带负电的试探电荷从$${{C}}$$点移到$${{E}}$$点，其电势能增加
1. 解析：
选项分析：
A. $$O$$点电场强度由$$A$$、$$B$$、$$C$$三电荷叠加。$$A$$和$$B$$在$$O$$点的场强大小相等、方向相反，抵消后仅剩$$-Q$$的场强，方向沿$$x$$轴负向，故$$O$$点场强不为零，A错误。
B. $$D$$点场强需计算三电荷的叠加。设$$AO = BO = d$$，则$$AD = BD = \sqrt{d^2 + (OD)^2}$$。由对称性，$$A$$和$$B$$在$$D$$点的场强竖直分量抵消，水平分量与$$-Q$$的场强叠加。若满足几何关系$$\angle ADO = 60^\circ$$，可推导出$$D$$点合场强为零，B正确。
C. 将$$+q$$从$$O$$移向$$C$$，需克服$$-Q$$的吸引力做功，电势能增大，C正确。
D. 将$$-q$$从$$O$$移向$$C$$，$$-Q$$对其吸引力做正功，D正确。
答案：BCD
2. 解析：
由动能$$E_k$$-$$x$$图像可知：
- 粒子从$$O$$向右运动时动能先增后减，说明$$Q_1$$在$$O$$左侧，$$Q_2$$在$$O$$右侧。
- 动能极大值点对应电场力为零的位置，即$$Q_1$$和$$Q_2$$的场强在此处平衡，故$$Q_1$$距离较远但电荷量较大。
选项B符合$$Q_1$$在左、$$Q_2$$在右且$$|Q_1| > |Q_2|$$的条件。
答案：B
3. 解析：
五个点电荷在$$O$$点的场强叠加：
- $$B$$、$$E$$和$$C$$、$$D$$的场强分别对称抵消。
- 剩余$$A$$点$$-q$$的场强大小为$$E_A = \frac{kq}{r^2}$$，方向沿$$OA$$向外。
- 其他四电荷$$+q$$的合场强大小为$$E_{合} = 2 \times \frac{kq}{r^2} \cos(72^\circ)$$，方向沿$$AO$$。
计算得总场强为$$\frac{2kq}{r^2}$$，方向沿$$AO$$。
答案：D
4. 解析：
半圆细线在$$O$$点的场强$$E$$由对称性可知，其方向沿对称轴。将细线分为三等分圆弧$$AB$$、$$BC$$、$$CD$$，每段在$$O$$点产生的场强大小相等。由矢量叠加，$$BC$$段的场强大小为$$E/3$$。
答案：C
5. 解析：
- $$O$$点场强由两对正负电荷叠加。设$$+Q$$在$$60^\circ$$位置，其场强与$$-Q$$的场强合成后大小为$$\frac{\sqrt{3}kQ}{R^2}$$，方向由$$O$$指向$$D$$，B正确。
- $$A$$、$$C$$两点电势：$$A$$点靠近$$+Q$$，电势高于$$C$$点（靠近$$-Q$$），C错误。
- 正电荷在$$A$$点的电势能大于在$$C$$点，D正确。
答案：BD
6. 解析：
- $$a$$、$$b$$两点关于$$+Q$$对称，场强大小相等但方向不同，电势相同（等势面为球面），A正确。
- $$c$$、$$d$$两点在匀强电场中，场强相同但电势沿电场线降低，D正确。
答案：AD
7. 解析：
电场是客观存在的，电荷$$A$$和$$B$$均激发电场，空间某点场强为两者场强的矢量和。D正确。
答案：D
8. 解析：
- $$O$$点场强由两$$+Q$$叠加，始终为零，A正确。
- 小球需克服重力做功，最小速度需满足$$\frac{1}{2}mv_0^2 \geq mgL$$，即$$v_0 \geq \sqrt{2gL}$$，B错误。
- 小球运动时，电场力可能随距离变化而减小，C正确。
- 电势能可能先增大（远离$$+Q$$）后减小（靠近另一$$+Q$$），D正确。
答案：ACD
9. 解析：
- 半球面电荷可视为完整球面的一半，其在$$P$$点的场强方向竖直向上（由对称性）。
- 电势计算：完整球面电势为$$2\pi k \sigma R$$，半球面电势减半，但$$P$$在开口处，电势与球面内相同，为$$2\pi k \sigma R$$。
答案：B
10. 解析：
- $$C$$点场强指向$$D$$，说明$$A$$点电荷为正，$$B$$点电荷为负，A正确。
- $$C$$、$$D$$两点场强方向不同，B错误。
- 由对称性，$$CE$$与$$ED$$电势差相等，C正确。
- 负电荷从$$C$$到$$E$$需克服电场力做功，电势能增加，D正确。
答案：ACD