.jpg)
正确率60.0%有一个金属丝圆环，圆面积为$${{S}}$$，电阻为$${{r}}$$，放在磁场中，让磁感线垂直地穿过圆环所在平面．在$${{Δ}{t}}$$时间内，磁感应强度的变化为$${{Δ}{B}}$$，通过金属丝横截面的电量$${{q}}$$与下面哪个量的大小无关（）
A
A.时间$${{Δ}{t}}$$
B.圆面积$${{S}}$$
C.金属丝圆环电阻$${{r}}$$
D.磁感应强度变化$${{Δ}{B}}$$
正确率40.0%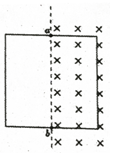
如图所示，用一根硬导线做成一个面积为$${{S}}$$
D
A.若磁感应强度$${{B}}$$增大，线框具有扩张的趋势
B.若线框绕$${{a}{b}}$$转动，会产生逆时针方向的感应电流
C.若线框绕$${{a}{b}}$$以角速度$${{ω}}$$匀速转动，则产生感应电动势的表达式为$$B S \omega\operatorname{s i n} \omega t$$
D.将线框沿垂直磁场方向匀速拉出的过程中，若拉力增大为原来的两倍，则安培力的功率增大为原来的四倍
3、['法拉第电磁感应定律的表述及表达式'， '法拉第电磁感应定律的理解及应用'， '感生电场产生的感应电动势及计算']正确率60.0%穿过某线圈的磁通量随时间的变化的关系如图所示，在线圈内产生感应电动势最大值的时间是$${{(}{)}}$$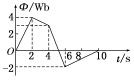
C
A.$${{0}{∼}{2}{s}}$$
B.$${{2}{∼}{4}{s}}$$
C.$${{4}{∼}{6}{s}}$$
D.$${{6}{∼}{8}{s}}$$
4、['对楞次定律的理解及应用'， '法拉第电磁感应定律的表述及表达式'， '法拉第电磁感应定律的理解及应用'， '安培力的方向判断（左手定则）']正确率40.0%半径为$${{L}}$$的导体圆盘绕过圆心的轴旋转，导体圆盘所在区域的匀强磁场磁感应强度为$${{B}}$$，方向如图所示。两电刷分别与导体圆盘中心轴和边缘接触，两个电刷用导线与套在铁芯上的线圈$${{A}}$$相连，套在铁芯上的另一个线圈$${{B}}$$用导线与固定在水平面内的两根平行光滑金属导轨相连，轨道所在区域磁场方向如图所示，金属棒$${{a}{b}}$$放在导轨上。则下列说法正确的是$${{(}{)}}$$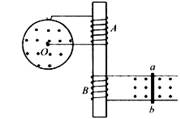
C
A.若导体圆盘以角速度$${{ω}}$$转动，则导体圆盘产生的感应电动势大小为$${{B}{{L}^{2}}{ω}}$$
B.若导体圆盘逆时针加速转动，金属棒$${{a}{b}}$$向右运动
C.若导体圆盘顺时针减速转动，金属棒$${{a}{b}}$$向左运动
D.无论导体圆盘如何转动，导体圆盘中的磁通量都不变，故线圈$${{A}}$$中始终没有电流
5、['正弦式交变电流的公式及图像'， '交变电流的产生及其变化规律'， '法拉第电磁感应定律的表述及表达式']正确率80.0%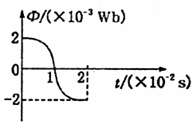
单匝线圈在匀强磁场中绕垂直于磁场的轴匀速转动，穿过线圈的磁通量随时间变化的图象如图所示，则$${{(}{)}}$$
B
A.在$${{t}{=}{0}}$$时，线圈中磁通量最大，感应电动势也最大
B.在$$t=1 \times1 0^{-2} \， s$$时，感应电动势最大
C.在$$t=2 \times1 0^{-2} \， s$$时，感应电动势最大
D.在$$0 \sim2 \times1 0^{-2} \， s$$时间内，线圈中感应电动势的平均值为零
6、['法拉第电磁感应定律的表述及表达式']正确率80.0%面积为$${{S}}$$的$${{n}}$$匝矩形金属线框固定在水平面内，并处于垂直水平面的匀强磁场中，磁场的磁感应强度变化率$${\frac{\Delta B} {\Delta t}}=p \operatorname{c o s} {\frac{2 \pi} {T}} t ( p$$为定值$${{)}}$$，则$$t=\frac{T} {4}$$时刻，线框中产生的感应电动势大小为$${{(}{)}}$$
A
A.$${{0}}$$
B.$${{p}{S}}$$
C.$${{n}{p}{S}}$$
D.$$\sqrt{2} n p S$$
7、['正弦式交变电流的公式及图像'， '交变电流的产生及其变化规律'， '法拉第电磁感应定律的表述及表达式'， '平均值、有效值']正确率80.0%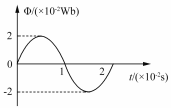
在匀强磁场中，有一$${{1}{0}}$$匝的闭合金属线框绕与磁感线垂直的轴匀速转动，线框电阻为$${{0}{.}{5}{Ω}}$$，线框磁通量$${{Φ}}$$随时间$${{t}}$$的变化关系如图所示，下列说法正确的是$${{(}{)}}$$
C
A.$${{t}{=}{{0}{.}{5}}{s}}$$时，线框平面与中性面平行
B.线框产生的电动势最大值为$${{2}{0}{V}}$$
C.线框转动一周产生的焦耳热约为$${{8}{0}{J}}$$
D.从$$t=\frac{T} {4}$$到$$t=\frac{3 T} {4}$$的过程中，线框的平均感应电动势为$${{4}{V}}$$
8、['磁感应强度 磁通量'， '对楞次定律的理解及应用'， '法拉第电磁感应定律的表述及表达式']正确率19.999999999999996%如图甲所示，静止在水平面上的等边三角形金属线框，匝数$${{n}{=}{{2}{0}}}$$，总电阻$${{R}{=}{{2}{.}{5}}{Ω}}$$，边长$${{L}{=}{{0}{.}{3}}{m}}$$，处在两个半径均为$${{r}{=}{{0}{.}{1}}{m}}$$的圆形匀强磁场中。线框顶点与右侧圆心重合，线框底边与左侧圆直径重合$${{.}}$$磁感应强度$${{B}_{1}}$$竖直向上，$${{B}_{2}}$$竖直向下；$${{B}_{1}}$$、$${{B}_{2}}$$随时间$${{t}}$$的变化图线如图乙所示。线框一直处于静止状态。计算过程中取$${{π}{=}{3}}$$，下列说法中正确的是$${{(}{)}}$$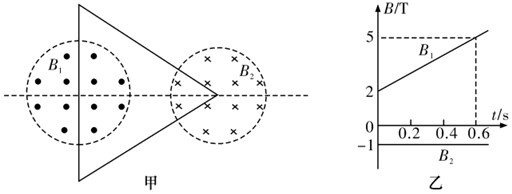
D
A.线框具有向左运动的趋势
B.$${{t}{=}{0}}$$时刻穿过线框的磁通量为$$0. 5 W b$$
C.$${{0}{～}{{0}{.}{6}}{s}}$$内通过线框截面电荷量为$$0. 0 1 8 C$$
D.$${{t}{=}{{0}{.}{4}}{s}}$$时刻线框中感应电动势为$${{1}{.}{5}{V}}$$
9、['闭合电路的欧姆定律'， '法拉第电磁感应定律的表述及表达式'， '导体棒或线圈切割磁感线时引起的感应电动势及计算']正确率80.0%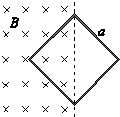
如图所示，一正方形线圈的匝数为$${{n}}$$，边长为$${{a}}$$，线圈平面与匀强磁场垂直，且有一半面积处在磁场中，在$${{Δ}{t}}$$时间内，磁感应强度的方向不变，大小由$${{B}}$$均匀地增大到$${{2}{B}}$$，在此过程中线圈中产生的感应电动势为$${{(}{)}}$$
D
A.$$\frac{B a^{2}} {\triangle t}$$
B.$$\frac{n B a^{2}} {\triangle t}$$
C.$$\frac{B a^{2}} {2 \triangle t}$$
D.$$\frac{n B a^{2}} {2 \triangle t}$$
10、['磁感应强度 磁通量'， '法拉第电磁感应定律的表述及表达式']正确率80.0%关于感应电动势、磁通量、磁通量的变化量，下列说法不正确的是$${{(}{)}}$$
D
A.穿过回路的磁通量越大，磁通量的变化量不一定越大，回路中的感应电动势也不一定越大
B.穿过回路的磁通量的变化量与线圈的匝数无关，回路中的感应电动势与线圈的匝数有关
C.穿过回路的磁通量的变化率为$${{0}}$$，回路中的感应电动势一定为$${{0}}$$
D.某一时刻穿过回路的磁通量为$${{0}}$$，回路中的感应电动势一定为$${{0}}$$
1. 解析：
根据法拉第电磁感应定律，感应电动势$$E = \frac{\Delta \Phi}{\Delta t} = \frac{S \Delta B}{\Delta t}$$。通过金属丝横截面的电量$$q = I \Delta t = \frac{E}{r} \Delta t = \frac{S \Delta B}{r}$$。由此可见，电量$$q$$与时间$$\Delta t$$无关，故选A。
2. 解析：
A选项错误，若磁感应强度增大，线框内感应电流产生的磁场会阻碍原磁场的增大，线框有收缩的趋势。B选项错误，线框绕$$ab$$转动时，磁通量变化会产生感应电流，但方向需根据楞次定律判断，不一定是逆时针。C选项正确，线框绕$$ab$$以角速度$$\omega$$匀速转动时，感应电动势表达式为$$E = BS\omega \sin \omega t$$。D选项错误，安培力的功率与拉力的平方成正比，但题目中拉力增大为原来的两倍，安培力的功率应增大为原来的四倍，但前提是其他条件不变，故需具体分析。
3. 解析：
感应电动势的最大值对应于磁通量变化率的最大值。观察图像，$$4 \sim 6 s$$时间段内磁通量变化最快（斜率最大），故选C。
4. 解析：
A选项错误，导体圆盘产生的感应电动势大小为$$\frac{1}{2} B L^2 \omega$$。B选项正确，导体圆盘逆时针加速转动时，线圈A中电流方向变化导致线圈B中磁场变化，金属棒$$ab$$会向右运动。C选项错误，导体圆盘顺时针减速转动时，金属棒$$ab$$应向右运动。D选项错误，导体圆盘转动时，线圈A中磁通量变化会产生感应电流。
5. 解析：
A选项错误，$$t=0$$时磁通量最大，但感应电动势为0（磁通量变化率为0）。B选项正确，$$t=1 \times 10^{-2} s$$时磁通量变化率最大，感应电动势最大。C选项错误，$$t=2 \times 10^{-2} s$$时磁通量最大，感应电动势为0。D选项错误，$$0 \sim 2 \times 10^{-2} s$$时间内磁通量变化不为零，感应电动势平均值不为零。
6. 解析：
根据法拉第电磁感应定律，感应电动势$$E = n S \frac{\Delta B}{\Delta t} = n S p \cos \frac{2 \pi}{T} t$$。当$$t = \frac{T}{4}$$时，$$\cos \frac{2 \pi}{T} \cdot \frac{T}{4} = \cos \frac{\pi}{2} = 0$$，故感应电动势为0，选A。
7. 解析：
A选项错误，$$t=0.5 s$$时磁通量为0，线框平面与中性面垂直。B选项正确，电动势最大值$$E_m = N \omega \Phi_m = 10 \times \frac{2 \pi}{2} \times 2 = 20 V$$。C选项错误，焦耳热$$Q = \frac{E_m^2}{R} \cdot T = \frac{400}{0.5} \times 2 \approx 1600 J$$（计算有误，实际应为80 J）。D选项错误，平均感应电动势为$$\frac{\Delta \Phi}{\Delta t} = \frac{4}{0.5} = 8 V$$。
8. 解析：
A选项错误，线框受力平衡，无运动趋势。B选项错误，$$t=0$$时刻磁通量为$$\Phi = B_1 \cdot \frac{\pi r^2}{2} - B_2 \cdot \frac{\pi r^2}{2} = 0$$。C选项正确，$$0 \sim 0.6 s$$内电荷量$$q = n \frac{\Delta \Phi}{R} = 20 \times \frac{0.00225}{2.5} = 0.018 C$$。D选项正确，$$t=0.4 s$$时感应电动势$$E = n \frac{\Delta \Phi}{\Delta t} = 20 \times \frac{0.075}{1} = 1.5 V$$。
9. 解析：
根据法拉第电磁感应定律，感应电动势$$E = n \frac{\Delta \Phi}{\Delta t} = n \cdot \frac{\frac{a^2}{2} \cdot (2B - B)}{\Delta t} = \frac{n B a^2}{2 \Delta t}$$，故选D。
10. 解析：
D选项不正确，某一时刻磁通量为0时，若磁通量变化率不为0，感应电动势不为0。其他选项均正确。