.jpg)
正确率40.0%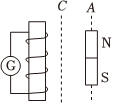
如图所示，条形磁铁与螺线管在同一平面内，条形磁铁由位置$${{A}}$$运动到位置$${{C}}$$，则$${{(}{)}}$$
A.若磁铁匀速运动，则电流计的示数不变
B.若磁铁加速运动，则电流计的示数比匀速过程的小
C.无论磁铁加速还是匀速运动，通过电流计的电荷量相同
D.无论磁铁加速还是匀速运动，电流计所在回路产生的焦耳热相同
2、['正弦式交变电流的公式及图像'， '交变电流的描述'， '焦耳定律']正确率80.0%两只相同的电阻，分别通以正弦波形的交变电流和方波形的交变电流，两种交变电流的最大值与周期相等$${{(}}$$如图甲、乙所示$${{)}}$$。在正弦波形交变电流的一个周期内，正弦波形的交变电流在电阻上产生的焦耳热为$${{Q}_{1}}$$，其与方波形交变电流在电阻上产生的焦耳热$${{Q}_{2}}$$之比，$${{Q}_{1}}$$：$${{Q}_{2}}$$等于$${{(}{)}}$$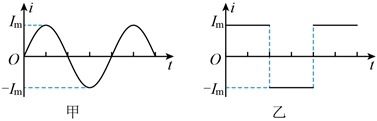
A.$${{1}}$$：$${{1}}$$
B.$${{2}}$$：$${{1}}$$
C.$${{1}}$$：$${{2}}$$
D.$${{3}}$$：$${{4}}$$
3、['焦耳定律'， '导体棒或线圈切割磁感线时引起的感应电动势及计算']正确率80.0%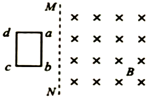
如图所示，纸面内有一矩形导体闭合线框动$${{a}{b}{c}{d}}$$，$${{a}{b}}$$边长大于$${{b}{c}}$$边长，置于垂直纸面向里、边界为$${{M}{N}}$$的匀强磁场外，线框两次匀速地完全进入磁场，两次速度大小相同，方向均垂直于$${{M}{N}{.}}$$第一次$${{a}{b}}$$边平行$${{M}{N}}$$进入磁场，线框上产生的热量为$${{Q}_{1}}$$，通过线框导体横截面的电荷量为$${{q}_{1}}$$；第二次$${{b}{c}}$$边平行$${{M}{N}}$$进入磁场．线框上产生的热量为$${{Q}_{2}}$$，通过线框导体横截面的电荷量为$${{q}_{2}}$$，则$${{(}{)}}$$
A.$${{Q}_{1}{=}{{Q}_{2}}}$$$${{q}_{1}{=}{{q}_{2}}}$$
B.$${{Q}_{1}{=}{{Q}_{2}}}$$$${{q}_{1}{>}{{q}_{2}}}$$
C.$${{Q}_{1}{>}{{Q}_{2}}}$$$${{q}_{1}{=}{{q}_{2}}}$$
D.$${{Q}_{1}{>}{{Q}_{2}}}$$$${{q}_{1}{>}{{q}_{2}}}$$
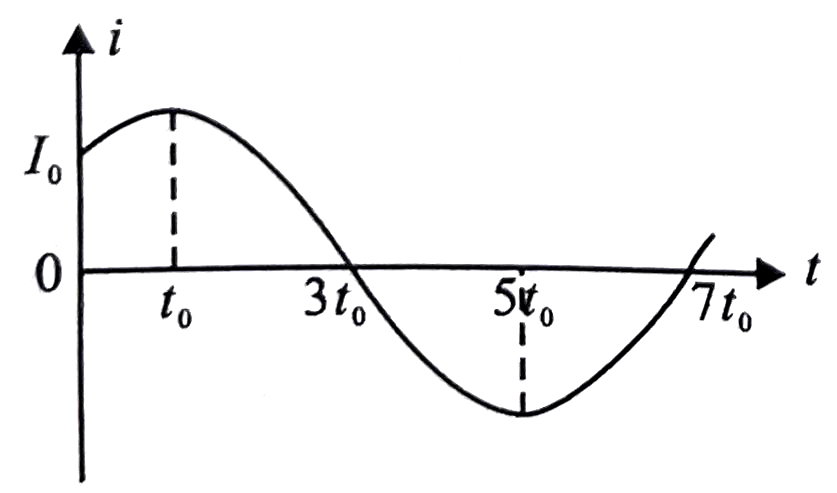
4、['焦耳定律'， '平均值、有效值']正确率80.0%如图是一个正弦式交变电流的波形图，当该电流通过阻值为$${{R}}$$的定值电阻时，在交流电的一个周期内，电阻$${{R}}$$上产生的焦耳热$${{Q}}$$为$${{(}{)}}$$
A.$${{2}{{I}^{2}_{0}}{R}{{t}_{0}}}$$
B.$${{4}{{I}^{2}_{0}}{R}{{t}_{0}}}$$
C.$${{8}{{I}^{2}_{0}}{R}{{t}_{0}}}$$
D.$$\mathbf{1 6} I_{0}^{2} \， R t_{0}$$
5、['磁感应强度 磁通量'， '法拉第电磁感应定律的表述及表达式'， '焦耳定律']正确率40.0%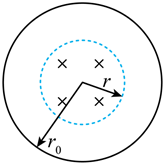
如图所示，半径为$${{r}_{0}}$$的圆形线圈共有$${{n}}$$匝，总电阻为$${{R}}$$，其中心位置处半径为$$r ( r < r_{0} )$$的虚线范围内有匀强磁场，磁场方向垂直线圈平面。若磁感应强度$${{B}}$$随时间变化的关系为$${{B}{=}{k}{t}}$$，则$${{(}{)}}$$
A.穿过线圈的磁通量为$${{n}{π}{B}{{r}^{2}}}$$
B.线圈中的磁通量的变化率为$${{n}{k}{π}{{r}^{2}}}$$
C.线圈中的感应电动势为$${{n}{k}{π}{{r}^{2}_{0}}}$$
D.$${{0}{～}{{t}_{0}}}$$时间内线圈中的焦耳热为$$\frac{( n k \pi r^{2} )^{2} t_{0}} {R}$$
6、['焦耳定律'， '平均值、有效值'， '周期和频率']正确率40.0%一电阻接到方波交流电源上，在一个周期内产生的热量为$$Q_{\pi}$$；若该电阻接到正弦交流电源上，在一个周期内产生的热量为$$Q_{\mathbb{T}}.$$该电阻上电压的峰值均为$${{u}_{0}}$$，周期均为$${{T}}$$，如图所示。则$$Q_{\pi}$$：$$Q_{\mathbb{T}}$$等于$${{(}{)}}$$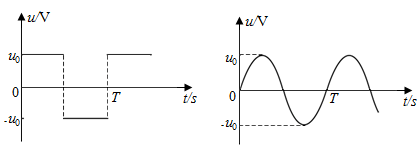
D
A.$${{1}}$$：$${\sqrt {2}}$$
B.$${\sqrt {2}}$$：$${{1}}$$
C.$${{1}}$$：$${{2}}$$
D.$${{2}}$$：$${{1}}$$
7、['正弦式交变电流的公式及图像'， '焦耳定律'， '平均值、有效值']正确率40.0%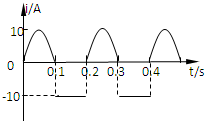
如图所示，为一交流电的电流随时间而变化的图象，此交流电流的有效值是$${{(}{)}}$$
B
A.$${{5}{\sqrt {2}}{A}}$$
B.$${{5}{\sqrt {3}}{A}}$$
C.$$\frac{9 \sqrt{2}} {2} A$$
D.$${{1}{0}{A}}$$
8、['焦耳定律'， '电功与电功率定义、表达式、物理意义及简单应用']正确率80.0%关于电功和电热，下面说法正确的是$${{(}{)}}$$
B
A.任何电路中的电功$$W=U I t$$，电热$$Q=I^{2} R t$$且$${{W}{=}{Q}}$$
B.任何电路中的电功$$W=U I t$$，电热$$Q=I^{2} R t$$且$${{W}}$$有时不等于$${{Q}}$$
C.电功$$W=U I t$$在任何电路中都适用，$$Q=I^{2} R t$$只在纯电阻电路中适用
D.电功$$W=U I t$$，电热$$Q=I^{2} R t$$，只适用于纯电阻电路
9、['焦耳定律'， '电路中的能量转化--非纯电阻电路']正确率40.0%
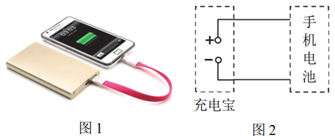
如图 $${{1}}$$ 所示，用充电宝为一手机电池充电，其等效电路如图 $${{2}}$$ 所示。在充电开始后的一段时间 $${{t}}$$ 内，充电宝的输出电压 $${{U}}$$ 、输出电流 $${{I}}$$ 可认为是恒定不变的，设手机电池的内阻为 $${{r}}$$ ，则时间 $${{t}}$$ 内 $${{(}{)}}$$
C
A.充电宝输出的电功率为$$U I+I^{2} r$$
B.充电宝产生的热功率为$${{I}^{2}{r}}$$
C.手机电池储存的化学能为$$U I t-I^{2} \mathrm{r t}$$
D.手机电池产生的焦耳热为$$\frac{U^{2}} {r} t$$
10、['正弦式交变电流的公式及图像'， '交变电流的描述'， '焦耳定律'， '平均值、有效值']正确率80.0%如图甲所示，有一匝数$${{N}{=}{{1}{0}{0}}}$$匝的矩形线圈在匀强磁场中绕垂直于磁场方向的轴匀速转动，从图示时刻开始计时，线圈中产生的交变电动势随时间变化的图像如图乙所示，已知线圈电阻$${{r}{=}{1}{Ω}}$$，电阻$${{R}{=}{{9}{9}}{Ω}}$$，则$${{(}{)}}$$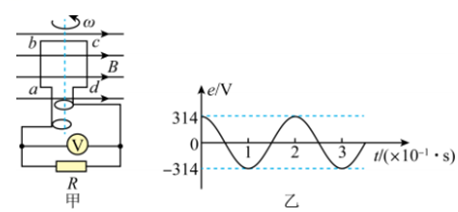
A.$${{t}{=}{{0}{.}{1}}{s}}$$时，线圈平面与磁感线垂直
B.$${{t}{=}{{0}{.}{0}{5}}{s}}$$时，电压表的示数为零
C.线圈从图示位置转过$${{9}{0}{°}}$$的过程中，通过电阻$${{R}}$$的电荷量为$${{0}{.}{1}{C}}$$
D.线圈转动一周的过程中，电阻$${{R}}$$产生的热量为$${{1}{9}{5}{J}}$$
1. 解析：当条形磁铁运动时，螺线管中会产生感应电流。感应电流的大小与磁通量的变化率有关，即 $$E = -\frac{d\Phi}{dt}$$。若磁铁匀速运动，磁通量变化率恒定，电流计示数不变（A正确）。若磁铁加速运动，磁通量变化率增大，电流计示数比匀速时大（B错误）。通过电流计的电荷量 $$q = \int I dt = \frac{\Delta \Phi}{R}$$，与运动方式无关（C正确）。焦耳热与电流平方和时间有关，加速运动时电流更大，焦耳热更多（D错误）。答案为 C。
2. 解析：正弦波电流的有效值 $$I_1 = \frac{I_0}{\sqrt{2}}$$，方波电流的有效值 $$I_2 = I_0$$。焦耳热 $$Q = I^2 R T$$，因此 $$Q_1 : Q_2 = \left(\frac{I_0}{\sqrt{2}}\right)^2 : I_0^2 = 1:2$$。答案为 C。
3. 解析：线框产生的热量 $$Q = \frac{(BLv)^2}{R} \cdot t$$，与边长无关，故 $$Q_1 = Q_2$$。通过电荷量 $$q = \frac{\Delta \Phi}{R}$$，与磁通量变化量有关，$$ab$$ 边长更大时磁通量变化量更大，故 $$q_1 > q_2$$。答案为 B。
4. 解析：正弦波电流的有效值 $$I = \frac{I_0}{\sqrt{2}}$$，周期 $$T = 4 t_0$$。焦耳热 $$Q = I^2 R T = \left(\frac{I_0}{\sqrt{2}}\right)^2 R \cdot 4 t_0 = 2 I_0^2 R t_0$$。答案为 A。
5. 解析：磁通量 $$\Phi = B \pi r^2$$（A错误）。磁通量变化率 $$\frac{d\Phi}{dt} = k \pi r^2$$（B错误）。感应电动势 $$E = n \frac{d\Phi}{dt} = n k \pi r^2$$（C错误）。焦耳热 $$Q = \frac{E^2}{R} t_0 = \frac{(n k \pi r^2)^2 t_0}{R}$$（D正确）。答案为 D。
6. 解析：方波电压有效值 $$U_{\pi} = u_0$$，正弦波电压有效值 $$U_{\mathbb{T}} = \frac{u_0}{\sqrt{2}}$$。焦耳热 $$Q = \frac{U^2}{R} T$$，因此 $$Q_{\pi} : Q_{\mathbb{T}} = u_0^2 : \left(\frac{u_0}{\sqrt{2}}\right)^2 = 2:1$$。答案为 D。
7. 解析：交流电有效值通过热效应等效计算。设周期为 $$T$$，前 $$T/2$$ 电流为 $$6\sqrt{2} A$$，后 $$T/2$$ 为 $$8\sqrt{2} A$$。有效值 $$I$$ 满足 $$I^2 R T = (6\sqrt{2})^2 R \cdot \frac{T}{2} + (8\sqrt{2})^2 R \cdot \frac{T}{2}$$，解得 $$I = 10 A$$。答案为 D。
8. 解析：电功 $$W = U I t$$ 适用于任何电路，电热 $$Q = I^2 R t$$ 也适用于任何电路，但 $$W = Q$$ 仅在纯电阻电路成立（B正确）。答案为 B。
9. 解析：充电宝输出功率 $$P = U I$$（A错误）。充电宝内阻未给出，无法计算其热功率（B错误）。手机电池储存化学能 $$E = U I t - I^2 r t$$（C正确）。手机电池焦耳热 $$Q = I^2 r t$$（D错误）。答案为 C。
10. 解析：$$t = 0.1 s$$ 时电动势为零，线圈平面与磁感线垂直（A正确）。电压表示数为有效值，始终不为零（B错误）。电荷量 $$q = N \frac{\Delta \Phi}{R + r} = 100 \cdot \frac{0.22}{100} = 0.22 C$$（C错误）。电阻 $$R$$ 的焦耳热 $$Q = \left(\frac{E}{\sqrt{2}(R + r)}\right)^2 R T = 195 J$$（D正确）。答案为 D。