.jpg)
正确率60.0%以下物理量和对应的比值定义式正确的是$${{(}{)}}$$
A.电场强度$$E=k {\frac{Q} {r^{2}}}$$
B.电流强度$$I=\frac{U} {R}$$
C.电容器电容$$C=\frac{Q} {U}$$
D.金属的电阻$$R=\rho\frac{l} {S}$$
2、['电流的微观表达式及其应用'， '阿伏加德罗常数及其应用'， '电源和电流']正确率80.0%有一条长为$${{l}}$$，横截面积为$${{S}}$$的银导线，银的密度为$${{ρ}}$$，银的摩尔质量为$${{M}}$$，阿伏加德罗常数为$${{N}_{A}}$$，若导线中每个银原子贡献一个自由电子，电子电荷量为$${{e}}$$，定向移动的速率为$${{v}}$$，通过导线的电流为$${{(}{)}}$$
A.$$I=\frac{N_{A} e v} {l}$$
B.$$I=\frac{\rho l e S v} {N_{A}}$$
C.$$I=\frac{\rho N_{A} e S v} {M}$$
D.$$I=\frac{M N_{A} e v} {\rho S}$$
3、['电流的微观表达式及其应用'， '欧姆定律适用条件及其计算'， '电阻定律'， '电源和电流']正确率80.0%
如图所示，两段长度和材料相同、各自粗细均匀的金属导线$${{a}}$$、$${{b}}$$，横截面积之比$${{S}_{a}}$$：$${{S}_{b}{=}{1}}$$：$${{2}}$$，已知$${{5}{s}}$$内有$$5 \times1 0^{1 8}$$个自由电子通过导线$${{a}}$$的横截面，电子的电荷量$$e=1. 6 \times1 0^{-1 9} C$$，下列说法正确的是$${{(}{)}}$$
A.流经导线$${{a}}$$的电流为$$0. 1 6 A$$
B.流经导线$${{b}}$$的电流为$$0. 3 2 A$$
C.导线$${{a}}$$、$${{b}}$$的电阻之比$${{R}_{a}}$$：$${{R}_{b}{=}{1}}$$：$${{2}}$$
D.导线$${{a}}$$、$${{b}}$$两端的电压之比$${{U}_{a}}$$：$${{U}_{b}{=}{1}}$$：$${{2}}$$
4、['电流的微观表达式及其应用'， '欧姆定律适用条件及其计算'， '电源和电流']正确率80.0%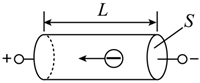
一根长为$${{L}}$$，横截面积为$${{S}}$$的金属棒，其材料的电阻率为$${{ρ}}$$，棒内单位体积内自由电子数为$${{n}}$$，电子的质量为$${{m}}$$、电荷量为$${{e}}$$，在棒两端加上恒定的电压$${{U}}$$，金属棒内自由电子定向移动的平均速率为$${{(}{)}}$$
A.$$\frac{U} {n e \rho L}$$
B.$$\frac{U_{S} \， S^{2}} {n e \rho L}$$
C.$${{n}{e}{ρ}{L}}$$
D.$$\frac{n e \rho S L} {U}$$
5、['闭合电路的欧姆定律'， '电源和电流'， '电功与电功率定义、表达式、物理意义及简单应用']正确率80.0%一定值电阻两端加上某一稳定电压，经一段时间通过该电阻的电荷量为$${{0}{.}{2}{C}}$$，消耗的电能为$${{0}{.}{6}{J}}$$。为在相同时间内使通过该电阻的电荷量为$${{0}{.}{6}{C}}$$，则在其两端需加的电压为$${{(}{)}}$$
D
A.$${{1}{V}}$$
B.$${{3}{V}}$$
C.$${{6}{V}}$$
D.$${{9}{V}}$$
6、['电流的微观表达式及其应用'， '欧姆定律适用条件及其计算'， '电源和电流']正确率80.0%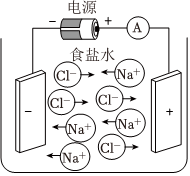
如图所示的电路可以测出电路中电荷定向移动的平均速率：水槽中$${{N}{a}{C}{l}}$$溶液的浓度为$$a ( m o l / m^{3} )$$，每一块矩形电极板的长为$${{b}}$$、宽为$${{c}}$$，电路稳定时电流表的读数为$${{I}}$$，阿伏加德罗常数为$${{N}_{A}}$$，元电荷为$${{e}}$$，则电荷定向移动的平均速率$${{v}}$$的表达式是$${{(}{)}}$$
A.$$v=\frac{I} {a N_{A} e b c}$$
B.$$v=\frac{I} {2 a N_{A} e b c}$$
C.$$v=\frac{I} {4 a N_{A} e b c}$$
D.$$v=\frac{2 I} {a N_{A} e b c}$$
7、['电流的微观表达式及其应用'， '欧姆定律适用条件及其计算'， '电阻定律'， '电源和电流']正确率80.0%一根粗细均匀的金属导线阻值为$${{R}}$$，两端加上恒定电压$${{U}}$$时，通过金属导线的电流强度为$${{I}}$$，金属导线中自由电子定向移动的平均速率为$${{v}}$$，若将金属导线均匀拉长，使其长度变为原来的$${{2}}$$倍，仍给它两端加上恒定电压$${{U}}$$，已知电流微观式为$$I=n e S V$$，其中$${{n}}$$为单位体积电子个数，$${{e}}$$为元电荷，$${{S}}$$为导线横截面积，则下列说法中正确的是$${{(}{)}}$$
A.此时金属导线的阻值为$${{2}{R}}$$
B.此时通过金属导线的电流为$$\frac{I} {2}$$
C.此时自由电子定向移动的平均速率为$$\frac{v} {2}$$
D.此时自由电子定向移动的平均速率为$$\frac{v} {4}$$
8、['电源和电流']正确率80.0%
均匀带电绝缘圆环所带电荷量为$${{Q}}$$。现使圆环绕垂直圆环所在平面且过圆心的轴以角速度$${{ω}}$$匀速转动。则环转动产生的等效电流为$${{(}{)}}$$
A.$${{Q}{ω}}$$
B.$$\frac{Q} {\omega}$$
C.$${{2}{π}{Q}{ω}}$$
D.$$\frac{Q \omega} {2 \pi}$$
9、['电源和电流'， '平均值、有效值'， '电功与电功率定义、表达式、物理意义及简单应用']正确率40.0%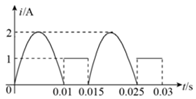
如图所示为一电流通过一电子元件后的波形图$${{(}}$$曲线部分为正弦交流电的一部分$${{)}}$$，则下列说法正确的是$${{(}{)}}$$
A.这是一种交变电流
B.电流的变化周期为$$0. 0 3 s$$
C.一个周期内流经电阻的电荷量大于$$0. 0 1 5 C$$
D.电流通过$${{1}{0}{0}{Ω}}$$电阻时，电功率为$${{1}{0}{0}{W}}$$
10、['电源和电流']正确率80.0%安培提出了著名的分子电流假说，根据这一假说，电子绕核运动可等效为一环形电流．设带电荷量为$${{e}}$$的电子以速率$${{v}}$$绕原子核沿顺时针方向做半径为$${{r}}$$的匀速圆周运动，其电流的等效电流强度$${{I}}$$和方向为$${{(}{)}}$$
C
A.$$\frac{e v} {2 \pi r}$$顺时针
B.$$\frac{v e} {r}$$顺时针
C.$$\frac{v e} {2 \pi r}$$逆时针
D.$$\frac{v e} {r}$$逆时针
1. 解析：
比值定义式是指用两个物理量的比值来定义一个新的物理量。
A. 电场强度 $$E$$ 的定义式为 $$E = \frac{F}{q}$$，而 $$E = k \frac{Q}{r^2}$$ 是点电荷电场的计算公式，不是比值定义式。
B. 电流强度 $$I$$ 的定义式为 $$I = \frac{q}{t}$$，而 $$I = \frac{U}{R}$$ 是欧姆定律的表达式，不是比值定义式。
C. 电容器电容 $$C$$ 的定义式为 $$C = \frac{Q}{U}$$，是比值定义式。
D. 金属电阻 $$R$$ 的定义式为 $$R = \rho \frac{l}{S}$$，是电阻的决定式，不是比值定义式。
正确答案是 C。
2. 解析：
电流 $$I$$ 的微观表达式为 $$I = n e S v$$，其中 $$n$$ 是单位体积的自由电子数。
银导线的质量 $$m = \rho l S$$，物质的量 $$n_{\text{mol}} = \frac{m}{M} = \frac{\rho l S}{M}$$。
自由电子总数 $$N = n_{\text{mol}} N_A = \frac{\rho l S N_A}{M}$$。
单位体积的自由电子数 $$n = \frac{N}{V} = \frac{\rho N_A}{M}$$。
代入电流公式得 $$I = \left( \frac{\rho N_A}{M} \right) e S v = \frac{\rho N_A e S v}{M}$$。
正确答案是 C。
3. 解析：
A. 通过导线 $$a$$ 的电流 $$I_a = \frac{q}{t} = \frac{5 \times 10^{18} \times 1.6 \times 10^{-19}}{5} = 0.16 \text{A}$$，正确。
B. 导线 $$a$$ 和 $$b$$ 串联，电流相同，$$I_b = I_a = 0.16 \text{A}$$，错误。
C. 电阻 $$R = \rho \frac{l}{S}$$，由于材料相同、长度相同，电阻与横截面积成反比，$$R_a : R_b = S_b : S_a = 2 : 1$$，错误。
D. 电压 $$U = IR$$，由于电流相同，电压与电阻成正比，$$U_a : U_b = R_a : R_b = 2 : 1$$，错误。
正确答案是 A。
4. 解析：
电流 $$I = \frac{U}{R}$$，电阻 $$R = \rho \frac{L}{S}$$，所以 $$I = \frac{U S}{\rho L}$$。
电流的微观表达式 $$I = n e S v$$，联立得 $$v = \frac{I}{n e S} = \frac{U}{n e \rho L}$$。
正确答案是 A。
5. 解析：
设电阻为 $$R$$，初始电压为 $$U_1$$，时间 $$t$$ 内电荷量 $$q_1 = I_1 t = 0.2 \text{C}$$，电能 $$W_1 = I_1^2 R t = 0.6 \text{J}$$。
由 $$q_1 = I_1 t$$ 得 $$I_1 = \frac{0.2}{t}$$，代入电能公式得 $$\left( \frac{0.2}{t} \right)^2 R t = 0.6$$，解得 $$R t = 15$$。
第二次电荷量 $$q_2 = I_2 t = 0.6 \text{C}$$，得 $$I_2 = \frac{0.6}{t}$$，电压 $$U_2 = I_2 R = \frac{0.6}{t} \times \frac{15}{t} = \frac{9}{t^2}$$。
由 $$R t = 15$$ 得 $$t = \frac{15}{R}$$，代入得 $$U_2 = 9 \left( \frac{R}{15} \right)^2$$，但更简单的方法是比例关系：电荷量变为 3 倍，电流也变为 3 倍，电压 $$U = IR$$ 也变为 3 倍，即 $$U_2 = 3 U_1$$。
初始电能 $$W_1 = U_1 I_1 t = U_1 \times 0.2 = 0.6$$，得 $$U_1 = 3 \text{V}$$，所以 $$U_2 = 9 \text{V}$$。
正确答案是 D。
6. 解析：
NaCl 溶液中，每个分子贡献 $$2$$ 个电荷（Na⁺ 和 Cl⁻），单位体积电荷数 $$n = 2 a N_A$$。
电流 $$I = n e S v$$，其中 $$S = b c$$，所以 $$v = \frac{I}{n e b c} = \frac{I}{2 a N_A e b c}$$。
正确答案是 B。
7. 解析：
导线拉长后，长度变为 $$2 l$$，体积不变，横截面积变为 $$\frac{S}{2}$$。
A. 电阻 $$R' = \rho \frac{2 l}{S/2} = 4 R$$，错误。
B. 电流 $$I' = \frac{U}{R'} = \frac{U}{4 R} = \frac{I}{4}$$，错误。
C. 电流微观式 $$I = n e S v$$，拉长后 $$I' = n e \left( \frac{S}{2} \right) v'$$，由 $$I' = \frac{I}{4}$$ 得 $$v' = \frac{v}{2}$$，正确。
D. 与 C 矛盾，错误。
正确答案是 C。
8. 解析：
等效电流是单位时间内通过某截面的电荷量。圆环转动一周的时间 $$T = \frac{2 \pi}{\omega}$$，电流 $$I = \frac{Q}{T} = \frac{Q \omega}{2 \pi}$$。
正确答案是 D。
9. 解析：
A. 电流方向不变，不是交变电流，错误。
B. 周期为 $$0.02 \text{s}$$（正弦部分半个周期为 $$0.01 \text{s}$$），错误。
C. 正半周电荷量 $$q_1 = \int_0^{0.01} I \sin(\omega t) dt$$，负半周电荷量 $$q_2 = 0$$（电流为 0），总电荷量 $$q = q_1 + q_2 > 0.015 \text{C}$$，正确。
D. 电流有效值需计算，但显然功率不为 $$100 \text{W}$$，错误。
正确答案是 C。
10. 解析：
电子运动周期 $$T = \frac{2 \pi r}{v}$$，等效电流 $$I = \frac{e}{T} = \frac{e v}{2 \pi r}$$。
电流方向与电子运动方向相反，为逆时针。
正确答案是 C。