.jpg)
正确率60.0%在电场中$${{A}}$$、$${{B}}$$两点间的电势差为$$U_{A B}=7 5 \mathrm{V}， \ B$$、$${{C}}$$两点间的电势差为$$U_{B C}=$$—$$2 0 0 \mathrm{V}，$$则$${{A}}$$、$${{B}}$$、$${{C}}$$三点的电势高低关系为（）
C
A.$$\varphi_{A} > \varphi_{B} > \varphi_{C}$$
B.$$\varphi_{A} < \varphi_{C} < \varphi_{B}$$
C.$$\varphi_{C} > \varphi_{A} > \varphi_{B}$$
D.$$\varphi_{C} > \varphi_{B} > \varphi_{A}$$
2、['匀强电场中电势差与电场强度的关系'， '电势差的计算'， '电场线（等势线）与带电粒子的运动轨迹问题']正确率40.0%
如图所示，以$${{O}}$$
B
A.粒子带负电
B.粒子由$${{M}}$$点运动到$${{N}}$$点，电势能先增大后减小
C.粒子在电场中可能从$${{M}}$$点沿圆弧运动到$${{N}}$$点
D.该匀强电场的电场强度大小为$$\frac{U} {R}$$
3、['匀强电场中电势差与电场强度的关系'， '电势差的计算'， '带电粒子在电场中的电势能']正确率40.0%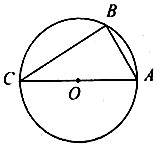
如图所示，真空中有一匀强电场（图中未画出），电场方向与圆周在同一平面内，$${{△}{A}{B}{C}}$$
C
A.圆周上$${{A}{、}{C}}$$两点的电势差为$${{8}{V}}$$
B.圆周上$${{B}{、}{C}}$$两点的电势差为$${{4}{V}}$$
C.匀强电场的场强大小为$$1 0 0 V / m$$
D.当某个粒子经过圆周上某一位置时，可以具有$${{6}{e}{V}}$$的电势能，且同时具有$${{6}{e}{V}}$$的动能
4、['电势差的计算'， '静电力做功与电势差的关系'， '静电平衡'， '点电荷的电场']正确率40.0%已知均匀带电的球壳在壳内任意一点产生的电场强度均为零，在壳外某点产生的电场强度等同于把壳上电量全部集中在球心处的点电荷所产生的电场强度.在真空中现有一半径为$${{R}{、}}$$电荷量为$${{+}{Q}}$$的均匀带电球，球心位置$${{O}}$$固定，$${{P}}$$为球外一点，$${{M}}$$为球内一点，如图所示，以无穷远为电势零点，关于$${{P}{、}{M}}$$两点的电场强度和电势，下列说法中正确的是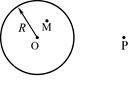
A
A.若$${{Q}}$$不变，$${{P}}$$点的位置也不变，而令$${{R}}$$变小，则$${{P}}$$点的场强不变
B.若$${{Q}}$$不变，$${{P}}$$点的位置也不变，而令$${{R}}$$变大$${{(}{P}}$$点仍在球外$${{)}}$$，则$${{P}}$$点的电势升高
C.若$${{Q}}$$不变，$${{M}}$$点的位置也不变，而令$${{R}}$$变小$${{(}{M}}$$点仍在球内$${{)}}$$，则$${{M}}$$点的电势不变
D.若$${{Q}}$$不变，$${{M}}$$点的位置也不变，而令$${{R}}$$变大，则$${{M}}$$点的场强减小
5、['电势差的计算'， '静电力做功'， '点电荷的电场']正确率60.0%如图所示，$$a， \， b， \， c， \， d. \， e$$五点在一直线上，$${{b}{、}{c}}$$两点间的距离等于$${{d}{、}{e}}$$两点间的距离。在$${{a}}$$点固定放置一个点电荷，带电荷量为$${{+}{Q}}$$，已知在$${{+}{Q}}$$的电场中$${{b}{、}{c}}$$两点间的电势差为$${{U}}$$，将另一个点电荷$${{+}{q}}$$从$${{d}}$$点移动到$${{e}}$$点的过程中，下列说法正确的是：
B
A.电场力做功等于$${{q}{U}}$$
B.电场力做功小于$${{q}{U}}$$
C.电场力做功大于$${{q}{U}}$$
D.克服电场力做功等于$${{q}{U}}$$
6、['匀强电场中电势差与电场强度的关系'， '电势差的计算'， '静电力做功与电势能的关系'， '等势面及其与电场线的关系'， '电势高低与电势能大小的判断']正确率40.0%如图所示，匀强电场中三点$$A， ~ B， ~ C$$是一个三角形的三个顶点，$$\angle A B C=\angle C A B=3 0^{\circ}， \， \， \， B C=2 \sqrt{3} m$$.已知电场线平行于$${{△}{A}{B}{C}}$$所在的平面，一个电荷量$$q=-1 \times1 0^{-6} C$$的点电荷由$${{A}}$$移到$${{B}}$$的过程中，电势能增加了$$1. 2 \times1 0^{-5} \， J$$，由$${{B}}$$移到$${{C}}$$的过程中电场力做功$$6 \times1 0^{-6} \， J$$，下列说法正确的是$${{(}{)}}$$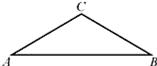
D
A.$${{B}{，}{C}}$$两点的电势差$$U_{B C}=3 ~ V$$
B.该电场的场强为$${{1}{V}{/}{m}}$$
C.$${{A}}$$点的电势低于$${{B}}$$点的电势
D.正电荷由$${{C}}$$点移到$${{A}}$$点的过程中，电势能增加
7、['匀强电场中电势差与电场强度的关系'， '电势差的概念及表达式'， '电势差的计算'， '电势能的概念及相对性'， '静电力做功与电势能的关系']正确率60.0%如图所示，相距为$${{1}{0}{c}{m}}$$的平行金属板$${{A}}$$和$${{B}}$$之间有一匀强电场，电场强度$$E=2 \times1 0^{4} V / m$$，方向向下。$${{C}}$$点距$${{B}}$$板$$3 c m， ~ D$$点距$${{A}}$$板$${{2}{c}{m}}$$，下列说法正确的是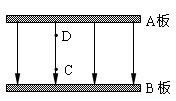
C
A.若$${{B}}$$板接地，则$$\varphi_{D}=-1 6 0 0 V$$
B.无论$${{A}}$$板还是$${{B}}$$板接地，$${{C}{D}}$$间的电势差始终为$$U_{C D}=1 0 0 0 V$$
C.若$${{A}}$$板接地，则置于$${{C}}$$处的带电量为$$1 0^{-8} C$$的正点电荷电势能为$$E_{p}=-1. 4 \times1 0^{-5} J$$
D.无论$${{A}}$$板还是$${{B}}$$板接地，将试探电荷从$${{D}}$$移动到$${{C}}$$其电势能都减小
8、['电势差的计算'， '根据电场线分析电场的分布特点'， '等势面及其与电场线的关系'， '电势高低与电势能大小的判断']正确率40.0%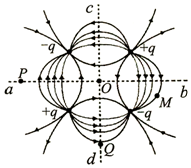
四个电荷量大小相同的点电荷位于正方形四个角上，电性与各点电荷附近的电场线分布如图所示．$$a b， ~ c d$$
D
A.$${{P}{、}{Q}}$$两点电势相等，场强也相等
B.$${{P}}$$点的电势比$${{M}}$$点的低
C.$${{P}{M}}$$两点间的电势差大于$${{Q}{M}}$$间的电势差
D.带负电的试探电荷在$${{Q}}$$点时比在$${{M}}$$点时电势能小
9、['非匀强电场中电势差与电场强度的关系'， '电势差的概念及表达式'， '电势差的计算'， '电势高低与电势能大小的判断']正确率40.0%
如图所示，$${{a}{、}{b}}$$
A
A.$${{a}}$$点比$${{b}}$$点间的电势高$$\frac{W} {q}$$
B.$${{a}}$$点的电场强度为$$E=\frac{W} {q d}$$
C.$${{b}}$$点的电场强度$$E=\frac{W} {q d}$$
D.$${{a}}$$点的电势为$$\frac{W} {q}$$
10、['匀强电场中电势差与电场强度的关系'， '电势差的计算']正确率40.0%如图所示，质量为$${{m}{、}}$$电量为$${{q}}$$的带电微粒，以初速度$${{V}_{0}}$$从$${{A}}$$点竖直向上射入水平方向$${、}$$电场强度为$${{E}}$$的匀强电场中。当微粒经过$${{B}}$$点时速率为$$V_{B}=2 V_{0}$$，而方向与$${{E}}$$同向。下列判断中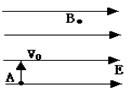
C
A.$${{A}{、}{B}}$$两点间电势差为$$2 m V_{0}^{2} / q$$
B.$${{A}{、}{B}}$$两点间的高度差为$$V_{0}^{2} / 2 g$$
C.微粒在$${{B}}$$点的电势能大于在$${{A}}$$点的电势能
D.从$${{A}}$$到$${{B}}$$微粒作匀变速运动
1. 解析：
由电势差定义 $$U_{AB} = \varphi_A - \varphi_B = 75\,\text{V}$$，得 $$\varphi_A > \varphi_B$$。
由 $$U_{BC} = \varphi_B - \varphi_C = -200\,\text{V}$$，得 $$\varphi_C > \varphi_B$$。
综上，$$\varphi_C > \varphi_A > \varphi_B$$，故选 C。
2. 解析：
图中电场线从 $$O$$ 指向 $$N$$，说明 $$O$$ 为高电势点，粒子由 $$M$$ 到 $$N$$ 运动时，电势能先增大（远离 $$O$$）后减小（靠近 $$O$$），选项 B 正确。
粒子不可能沿圆弧运动（电场力方向变化），选项 C 错误。
电场强度 $$E = \frac{U}{R}$$ 仅适用于匀强电场直线距离，此处不适用，选项 D 错误。
故选 B。
3. 解析：
由题意，$$U_{AB} = 12\,\text{V}$$，$$U_{BC} = -12\,\text{V}$$，说明 $$A$$ 和 $$C$$ 电势相等，$$U_{AC} = 0$$，选项 A 错误。
$$B$$ 点电势介于 $$A$$ 和 $$C$$ 之间，$$U_{BC} = -12\,\text{V}$$，选项 B 错误。
电场强度 $$E = \frac{U_{AB}}{d} = \frac{12}{0.12} = 100\,\text{V/m}$$，选项 C 正确。
粒子总能量守恒，可以同时具有 $$6\,\text{eV}$$ 的电势能和动能，选项 D 正确。
故选 CD。
4. 解析：
球壳外场强 $$E_P = \frac{kQ}{r_P^2}$$，与 $$R$$ 无关，选项 A 正确。
$$P$$ 点电势 $$\varphi_P = \frac{kQ}{r_P}$$，$$R$$ 变大时 $$\varphi_P$$ 不变，选项 B 错误。
球内电势 $$\varphi_M = \frac{kQ}{R}$$，$$R$$ 变小时 $$\varphi_M$$ 升高，选项 C 错误。
球内场强 $$E_M = 0$$，与 $$R$$ 无关，选项 D 错误。
故选 A。
5. 解析：
点电荷电场中，电势差随距离增大而减小。$$d,e$$ 比 $$b,c$$ 离 $$a$$ 更远，$$U_{de} < U_{bc} = U$$，电场力做功 $$W = qU_{de} < qU$$，故选 B。
6. 解析：
由 $$W_{BC} = qU_{BC}$$，得 $$U_{BC} = \frac{6 \times 10^{-6}}{-1 \times 10^{-6}} = -6\,\text{V}$$，选项 A 错误。
$$A$$ 到 $$B$$ 电势能增加，说明 $$q$$ 从低电势到高电势，即 $$\varphi_A < \varphi_B$$，选项 C 正确。
电场强度 $$E = \frac{U_{AB}}{d} = \frac{12}{2\sqrt{3} \sin 30^\circ} = 4\,\text{V/m}$$，选项 B 错误。
$$C$$ 到 $$A$$ 电势降低，正电荷电势能减少，选项 D 错误。
故选 C。
7. 解析：
$$B$$ 板接地时，$$\varphi_D = -E \cdot d_D = -2 \times 10^4 \times 0.02 = -400\,\text{V}$$，选项 A 错误。
$$U_{CD} = E \cdot d_{CD} = 2 \times 10^4 \times 0.05 = 1000\,\text{V}$$，与接地无关，选项 B 正确。
$$A$$ 板接地时，$$\varphi_C = E \cdot d_C = 2 \times 10^4 \times 0.03 = 600\,\text{V}$$，电势能 $$E_p = q\varphi_C = 10^{-8} \times 600 = 6 \times 10^{-6}\,\text{J}$$，选项 C 错误。
从 $$D$$ 到 $$C$$，电势升高，正电荷电势能减小，选项 D 正确。
故选 BD。
8. 解析：
$$P$$ 和 $$Q$$ 为对称点，电势相等，但场强方向不同，选项 A 错误。
$$P$$ 靠近负电荷，电势比 $$M$$ 低，选项 B 正确。
$$PM$$ 间电场线更密集，电势差更大，选项 C 正确。
$$Q$$ 点电势高于 $$M$$ 点，负电荷在 $$Q$$ 点电势能更小，选项 D 正确。
故选 BCD。
9. 解析：
由功与电势差关系 $$W = qU_{ab}$$，得 $$U_{ab} = \frac{W}{q}$$，选项 A 正确。
场强 $$E = \frac{U_{ab}}{d} = \frac{W}{q d}$$，选项 B 正确，C 错误。
电势为相对值，无法确定 $$\varphi_a$$ 具体值，选项 D 错误。
故选 AB。
10. 解析：
由动能定理，$$qU_{AB} + mgh = \frac{1}{2}m(2V_0)^2 - \frac{1}{2}mV_0^2$$。
竖直方向 $$h = \frac{V_0^2}{2g}$$，选项 B 正确。
水平方向 $$qU_{AB} = \frac{3}{2}mV_0^2 - mgh = mV_0^2$$，得 $$U_{AB} = \frac{mV_0^2}{q}$$，选项 A 错误。
微粒电势能减少，选项 C 错误。
微粒受恒力，做匀变速运动，选项 D 正确。
题目要求选不正确的，故选 AC。