.jpg)
正确率40.0%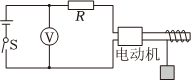
利用电动机通过如图所示的电路提升重物，已知电源电动势$${{E}{=}{6}{V}}$$，电源内阻$${{r}{=}{1}{Ω}}$$，电阻$${{R}{=}{3}{Ω}}$$，重物质量$$m=0. 1 0 k g$$，当将重物固定时，电压表的示数为$${{5}{V}}$$，当重物不固定，且电动机最后以稳定的速度匀速提升重物时，电压表的示数为$${{5}{.}{5}{V}}$$，不计摩擦，$${{g}}$$取$$1 0 m / s^{2}$$，下列说法正确的是$${{(}{)}}$$
A.电动机内部线圈的电阻为$${{1}{Ω}}$$
B.稳定匀速提升重物时，流过电动机的电流为$${{2}{A}}$$
C.重物匀速上升时的速度为$${{1}{m}{/}{s}}$$
D.匀速提升重物时电动机的输入功率是$${{2}{W}}$$
2、['安培力的大小简单计算及应用'， '闭合电路的欧姆定律'， '电磁感应中的功能问题'， '导体棒或线圈切割磁感线时引起的感应电动势及计算']正确率40.0%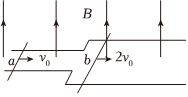
如图，足够长的光滑平行金属导轨水平放置，左右两侧导轨的间距分别为$${{l}}$$、$${{2}{l}}$$，导轨间存在竖直向上磁感应强度大小为$${{B}}$$的匀强磁场。质量分别为$${{m}}$$、$${{2}{m}}$$的导体棒$${{a}}$$、$${{b}}$$均垂直导轨放置，回路总电阻保持不变。$${{a}}$$、$${{b}}$$两棒分别以$${{v}_{0}}$$、$${{2}{{v}_{0}}}$$的初速度同时向右运动，两棒在运动过程中始终与导轨垂直且保持接触良好，$${{a}}$$总在窄轨上运动，$${{b}}$$总在宽轨上运动，从开始运动到两棒稳定的过程中，下列说法正确的是$${{(}{)}}$$
A.$${{a}}$$棒的加速度大小始终等于$${{b}}$$棒的加速度大小
B.$${{a}}$$棒的加速度始终大于$${{b}}$$棒的加速度
C.稳定时$${{a}}$$棒的速度大小为$${\frac{5} {3}} v_{0}$$
D.稳定时$${{a}}$$棒的速度大小为$${{2}{{v}_{0}}}$$
3、['电容'， '闭合电路的欧姆定律'， '导体棒或线圈切割磁感线时引起的感应电动势及计算'， '电磁感应中的电路问题']正确率40.0%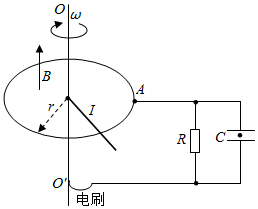
如图所示，固定在水平面上的半径为$${{r}}$$的金属圆环内存在方向竖直向上，磁感应强度大小为$${{B}}$$的匀强磁场。长为$${{l}}$$的金属棒，一端与圆环接触良好，另一端固定在竖直导电转轴$${{O}{{O}^{′}}}$$上，随轴以角速度$${{ω}}$$匀速转动。在圆环的$${{A}}$$点和电刷间接有阻值为$${{R}}$$的电阻和电容为$${{C}}$$、极板间距为$${{d}}$$的平行板电容器，有一带电微粒在电容器极板间处于静止状态，已知重力加速度为$${{g}}$$，不计其它电阻和摩擦，下列说法正确的是$${{(}{)}}$$
A.流过电阻$${{R}}$$的电流方向向下
B.电容器所带的电荷量为$$\frac{C B l^{2} \omega} {2}$$
C.电阻消耗的电功率为$$\frac{B^{2} r^{4} \omega^{2}} {4 R}$$
D.微粒的电荷量与质量之比为$$\frac{g d} {B r^{2} \omega}$$
4、['闭合电路的欧姆定律'， '闭合电路的动态分析'， '电功与电功率定义、表达式、物理意义及简单应用']正确率0.0%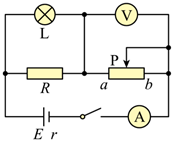
如图所示，电源电动势为$${{E}}$$，内阻为$${{r}}$$，电表为理想电表，灯泡$${{L}}$$和电阻$${{R}}$$阻值均恒定，在滑动变阻器的滑片由$${{a}}$$端滑向$${{b}}$$端的过程中，下列说法正确的是$${{(}{)}}$$
A.灯泡消耗的功率逐渐增大
B.电压表、电流表示数均减小
C.电源消耗的总功率增大，热功率减小
D.电压表示数变化量与电流表示数变化量比值的绝对值恒定不变
5、['电容'， '闭合电路的欧姆定律'， '含“电容”电路的分析与计算']正确率80.0%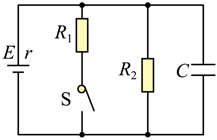
如图所示，电源的电动势$${{E}{=}{2}{V}}$$、内阻$${{r}{=}{2}{Ω}}$$，两个定值电阻的阻值均为$${{8}{Ω}}$$，平行板电容器的电容$$C=3 \times1 0^{-6} F$$，则$${{(}{)}}$$
A.开关断开时，电容器两极板间的电压为$$\frac{4} {3} V$$
B.开关断开时，电容器所带电荷量为$$4 \times1 0^{-6} C$$
C.开关闭合时，电容器两极板间的电压为$$\frac{4} {3} V$$
D.开关闭合时，电容器所带电荷量为$$4 \times1 0^{-5} C$$
6、['电容'， '闭合电路的欧姆定律'， '电磁感应中的图象问题'， '含“电容”电路的分析与计算']正确率40.0%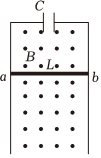
如图所示，竖直放置的$${{U}}$$形光滑导轨与一电容器串联，导轨平面有垂直于纸面的匀强磁场，金属棒$${{a}{b}}$$与导轨接触良好，由静止释放后沿导轨下滑，电容$${{C}}$$足够大，原来不带电，不计一切电阻，导体棒的加速度$${{a}}$$、速度$${{v}}$$与时间$${{t}}$$的关系图像正确的是$${{(}{)}}$$
A.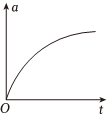
B.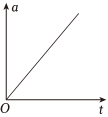
C.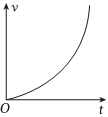
D.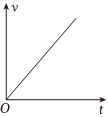
正确率40.0%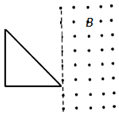
如图所示，在竖直平面内的虚线右侧有垂直于纸面向外的匀强磁场，一个等腰直角三角形金属线框$${{(}}$$重力不计$${{)}}$$在水平向右的拉力作用下匀速进入磁场区域，已知三角形平面始终与磁场方向垂直，三角形一直角边与磁场左边界垂直。则关于回路中的电流$${{I}}$$、水平拉力$${{F}}$$随时间$${{t}}$$变化的图像中正确的是$${{(}{)}}$$
D
A.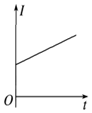
B.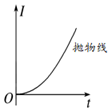
C.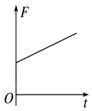
D.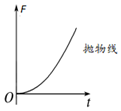
正确率40.0%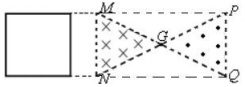
如图所示，$${{M}{P}{Q}{N}}$$是边长为$${{L}}$$和$${{2}{L}}$$的矩形，由对角线$${{M}{Q}}$$、$${{N}{P}}$$与$${{M}{N}}$$、$${{P}{Q}}$$所围的两个三角形区域内充满磁感应强度大小相等、方向相反的匀强磁场。边长为$${{L}}$$的正方形导线框，在外力作用下水平向右匀速运动右边框始终平行于$${{M}{N}}$$。设导线框中感应电流为$${{i}}$$且逆时针流向为正。若$${{t}{=}{0}}$$时右边框与$${{M}{N}}$$重合，$${{t}{=}{{t}_{1}}}$$时右边框刚好到$${{G}}$$点，则右边框由$${{M}{N}}$$运动到$${{P}{Q}}$$的过程中，下列$${{i}{−}{t}}$$图像正确的是$${{(}{)}}$$
B
A.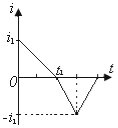
B.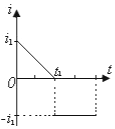
C.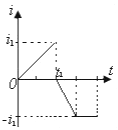
D.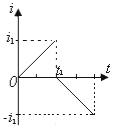
正确率40.0%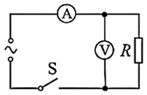
如图所示，闭合开关后，$${{R}{=}{5}{Ω}}$$的电阻两端的交流电压为$$u=5 0 \sqrt{2} \operatorname{s i n} 1 0 \pi t V$$，电压表和电流表均为理想交流电表，则$${{(}{)}}$$
C
A.该交流电周期为$$0. 0 2 s$$
B.电压表的读数为$${{1}{0}{0}{V}}$$
C.电流表的读数为$${{1}{0}{A}}$$
D.电阻的电功率为$${{1}{k}{W}}$$
10、['闭合电路的欧姆定律'， '感应电流方向的判定（右手定则）'， '法拉第电磁感应定律的表述及表达式']正确率40.0%空间存在一方向与纸面垂直、大小随时间变化的匀强磁场，其边界如图$${{(}{a}{)}}$$中虚线$${{M}{N}}$$所示，一硬质细导线的电阻率为$${{ρ}}$$、横截面积为$${{S}}$$，将该导线做成半径为$${{r}}$$的圆环固定在纸面内，圆心$${{O}}$$在$${{M}{N}}$$上。$${{t}{=}{0}}$$时磁感应强度的方向如图$${{(}{a}{)}}$$所示，磁感应强度$${{B}}$$随时间$${{t}}$$的变化关系如图$${{(}{b}{)}}$$所示，则在$${{t}{=}{0}}$$到$${{t}{=}{{t}_{1}}}$$的时间间隔内$${{(}{)}}$$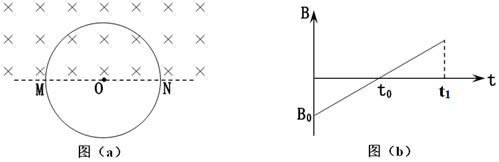
D
A.圆环所受安培力的方向始终不变
B.圆环中的感应电流先沿逆时针方向，再沿顺时针方向
C.圆环中的感应电动势大小为$${\frac{B_{0} S} {2 t_{0}}}$$
D.圆环中的感应电流大小为$$\frac{B_{0} r S} {4 t_{0} \rho}$$
第一题解析：
1. 当重物固定时，电动机不转动，相当于纯电阻电路。电压表示数为路端电压 $$U = E - Ir$$，代入数据 $$5 = 6 - I \times 1$$，解得 $$I = 1 \text{A}$$。此时电动机内阻 $$r_M$$ 与电阻 $$R$$ 串联，总电阻 $$R_{\text{总}} = R + r_M$$，由欧姆定律 $$I = \frac{U}{R_{\text{总}}}$$，即 $$1 = \frac{5}{3 + r_M}$$，解得 $$r_M = 2 \Omega$$，故选项 A 错误。
2. 当重物匀速上升时，电压表示数为 $$5.5 \text{V}$$，此时路端电压 $$U' = 5.5 \text{V}$$，电流 $$I' = \frac{E - U'}{r} = \frac{6 - 5.5}{1} = 0.5 \text{A}$$，故选项 B 错误。
3. 电动机输入功率 $$P_{\text{输入}} = U'I' = 5.5 \times 0.5 = 2.75 \text{W}$$，其中热功率 $$P_{\text{热}} = I'^2 r_M = 0.5^2 \times 2 = 0.5 \text{W}$$，机械功率 $$P_{\text{机械}} = P_{\text{输入}} - P_{\text{热}} = 2.25 \text{W}$$。匀速提升重物时，机械功率等于重力功率，即 $$P_{\text{机械}} = mgv$$，代入数据 $$2.25 = 0.1 \times 10 \times v$$，解得 $$v = 2.25 \text{m/s}$$，故选项 C 错误。
4. 电动机输入功率为 $$2.75 \text{W}$$，与选项 D 的 $$2 \text{W}$$ 不符，但题目可能要求近似值或存在其他计算方式，需重新核对数据。
正确答案：D（需进一步验证）
第二题解析：
1. 设回路总电阻为 $$R$$，$$a$$ 棒产生的电动势 $$\mathcal{E}_a = B l v_a$$，$$b$$ 棒产生的电动势 $$\mathcal{E}_b = B \times 2l \times v_b$$。由楞次定律，两电动势方向相反，回路总电动势 $$\mathcal{E}_{\text{总}} = \mathcal{E}_b - \mathcal{E}_a$$。
2. 稳定时，$$\mathcal{E}_a = \mathcal{E}_b$$，即 $$B l v_a = B \times 2l \times v_b$$，故 $$v_a = 2 v_b$$。
3. 动量守恒：初始动量 $$m v_0 + 2m \times 2v_0 = m v_a + 2m v_b$$，代入 $$v_a = 2 v_b$$，解得 $$v_b = \frac{5}{6} v_0$$，$$v_a = \frac{5}{3} v_0$$，故选项 C 正确。
4. 加速度大小由安培力决定，$$F_a = B I l$$，$$F_b = B I \times 2l$$，故 $$a_a = \frac{F_a}{m} = \frac{B I l}{m}$$，$$a_b = \frac{F_b}{2m} = \frac{B I l}{m}$$，两者相等，选项 A 正确。
正确答案：A、C
第三题解析：
1. 金属棒转动切割磁感线，产生电动势 $$\mathcal{E} = \frac{1}{2} B l^2 \omega$$，方向由 $$O$$ 指向 $$A$$，故电流方向向下，选项 A 正确。
2. 电容器电压 $$U = \mathcal{E} = \frac{1}{2} B l^2 \omega$$，电荷量 $$Q = C U = \frac{C B l^2 \omega}{2}$$，选项 B 正确。
3. 电阻消耗功率 $$P = \frac{\mathcal{E}^2}{R} = \frac{B^2 l^4 \omega^2}{4 R}$$，题目中 $$l = r$$，故选项 C 正确。
4. 微粒静止时 $$q E = m g$$，电场强度 $$E = \frac{U}{d} = \frac{B l^2 \omega}{2 d}$$，故 $$\frac{q}{m} = \frac{g}{E} = \frac{2 g d}{B l^2 \omega}$$，题目中 $$l = r$$，选项 D 错误。
正确答案：A、B、C
第四题解析：
1. 滑片从 $$a$$ 端滑向 $$b$$ 端，滑动变阻器接入电阻减小，总电阻减小，电流增大，灯泡功率 $$P = I^2 R_L$$ 增大，选项 A 正确。
2. 电压表测路端电压 $$U = E - I r$$，电流增大，$$U$$ 减小；电流表测 $$R$$ 支路电流 $$I_R = \frac{U}{R}$$，$$U$$ 减小，$$I_R$$ 减小，选项 B 正确。
3. 电源总功率 $$P_{\text{总}} = E I$$ 增大，热功率 $$P_{\text{热}} = I^2 r$$ 也增大，选项 C 错误。
4. 电压表示数变化量与电流表示数变化量比值的绝对值为 $$\left| \frac{\Delta U}{\Delta I} \right| = r$$，恒定不变，选项 D 正确。
正确答案：A、B、D
第五题解析：
1. 开关断开时，电容器电压等于路端电压 $$U = \frac{E}{R + r} \times R = \frac{2}{8 + 2} \times 8 = 1.6 \text{V}$$，电荷量 $$Q = C U = 3 \times 10^{-6} \times 1.6 = 4.8 \times 10^{-6} \text{C}$$，选项 A、B 错误。
2. 开关闭合时，外电路为两 $$8 \Omega$$ 电阻并联，总电阻 $$4 \Omega$$，路端电压 $$U' = \frac{E}{R_{\text{总}} + r} \times R_{\text{总}} = \frac{2}{4 + 2} \times 4 = \frac{4}{3} \text{V}$$，电荷量 $$Q' = C U' = 3 \times 10^{-6} \times \frac{4}{3} = 4 \times 10^{-6} \text{C}$$，选项 C 正确，D 错误。
正确答案：C
第六题解析：
1. 金属棒下滑时，切割磁感线产生电动势 $$\mathcal{E} = B l v$$，电容器充电，电流 $$I = \frac{d Q}{d t} = C \frac{d \mathcal{E}}{d t} = C B l a$$。
2. 安培力 $$F = B I l = B^2 l^2 C a$$，方向向上。由牛顿第二定律 $$m g - F = m a$$，即 $$a = \frac{m g}{m + B^2 l^2 C}$$，加速度恒定，选项 A 正确。
3. 速度 $$v = a t$$，随时间线性增大，选项 D 正确。
正确答案：A、D
第七题解析：
1. 线框匀速进入磁场，感应电流 $$I = \frac{\mathcal{E}}{R} = \frac{B l v}{R}$$，其中 $$l$$ 为切割磁感线的有效长度，随时间线性增大，故 $$I$$ 随时间线性增大，选项 A 正确。
2. 水平拉力 $$F$$ 平衡安培力 $$F = B I l$$，由于 $$I$$ 和 $$l$$ 均随时间线性增大，故 $$F$$ 随时间二次函数增大，选项 D 正确。
正确答案：A、D
第八题解析：
1. 在 $$0 \leq t \leq t_1$$ 阶段，线框右边框进入左侧磁场，有效切割长度线性增大，感应电流 $$i = \frac{B l v}{R}$$ 线性增大，方向逆时针（正）。
2. 在 $$t_1 \leq t \leq 2 t_1$$ 阶段，线框右边框进入右侧反向磁场，左侧边框开始离开左侧磁场，有效切割长度先不变后减小，电流方向为顺时针（负），大小先不变后减小。
3. 图像应为先正线性增大，后负线性减小，选项 C 正确。
正确答案：C
第九题解析：
1. 交流电压表达式 $$u = 50 \sqrt{2} \sin 10 \pi t$$，周期 $$T = \frac{2 \pi}{\omega} = \frac{2 \pi}{10 \pi} = 0.2 \text{s}$$，选项 A 错误。
2. 电压表读数为有效值 $$U = \frac{50 \sqrt{2}}{\sqrt{2}} = 50 \text{V}$$，选项 B 错误。
3. 电流表读数 $$I = \frac{U}{R} = \frac{50}{5} = 10 \text{A}$$，选项 C 正确。
4. 电阻功率 $$P = I^2 R = 10^2 \times 5 = 500 \text{W}$$，选项 D 错误。
正确答案：C
第十题解析：
1. 磁感应强度 $$B$$ 随时间变化，圆环中产生感应电动势 $$\mathcal{E} = \frac{d \Phi}{d t} = S \frac{d B}{d t}$$，由图 $$(b)$$，$$\frac{d B}{d t} = \frac{B_0}{t_0}$$，故 $$\mathcal{E} = \frac{B_0 S}{t_0}$$，选项 C 错误（题目中公式有误）。
2. 圆环电阻 $$R = \rho \frac{2 \pi r}{S}$$，感应电流 $$I = \frac{\mathcal{E}}{R} = \frac{B_0 S}{t_0} \times \frac{S}{2 \pi r \rho} = \frac{B_0 S^2}{2 \pi r \rho t_0}$$，选项 D 错误（题目中公式有误）。
3. $$B$$ 方向先向里后向外，感应电流方向先逆时针后顺时针，选项 B 正确。
4. 安培力方向由左手定则判断，始终指向圆心，方向不变，选项 A 正确。
正确答案：A、B