.jpg)
正确率40.0%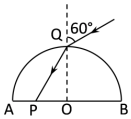
半径为$${{R}}$$
B
A.$$\frac{3 R} {2 c}$$
B.$$\frac{2 R} {c}$$
C.$$\frac{\sqrt3 R} {c}$$
D.$$\frac{2 \sqrt{3} R} {3 c}$$
2、['临界角'， '折射率定义式及物理意义'， '全反射现象'， '折射率的波长表达式和速度表达式']正确率40.0%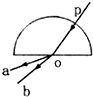
$${{P}}$$
D
A.玻璃对$${{a}}$$光的折射率小于对$${{b}}$$光的折射率
B.$${{a}}$$光频率小于$${{b}}$$光频率
C.在玻璃砖中传播的时间$${{a}}$$光比$${{b}}$$光短
D.若让玻璃砖在纸面内绕$${{O}}$$点逆时针转动，$${{a}}$$光先消失
3、['临界角'， '全反射定义、条件等相关概念'， '折射率定义式及物理意义']正确率40.0%如图，$${{A}}$$光束由红光和蓝光组成经过半圆形玻璃砖后分为$${{P}{、}{Q}}$$两束，关于$${{P}{、}{Q}}$$两束光下列叙述正确的是$${{(}{)}}$$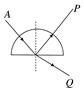
D
A.$${{P}}$$光束只有蓝光
B.$${{P}}$$光束只有红光
C.$${{Q}}$$光束只有蓝光
D.$${{Q}}$$光束只有红光
4、['折射率定义式及物理意义']正确率60.0%安庆市$${{K}}$$广场灯光音乐喷泉的水池中，有处于同一深度的若干彩灯，晚上在彩灯上方附近观察不同颜色彩灯的深度会有所不同，假设所有彩灯均视为点光源，现就红光灯和绿光灯比较，下列说法正确的是$${{(}{)}}$$
D
A.红灯看起来较浅，因为红光折射率较大
B.绿灯看起来较浅，因为绿光折射率较小
C.绿灯看起来较深，因为绿光折射率较大
D.红灯看起来较深，因为红光折射率较小
5、['折射率定义式及物理意义'， '折射定律的内容及表达式']正确率60.0%如图所示，有一玻璃三棱镜$${{A}{B}{C}}$$，顶角$${{A}}$$为$${{3}{0}^{∘}}$$，一束光线垂直于$${{A}{B}}$$射入棱镜，从$${{A}{C}}$$射出进入空气，测得出射光线与$${{A}{C}}$$夹角为$${{3}{0}^{∘}}$$，则棱镜的折射率为（）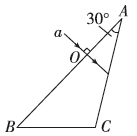
C
A.$$\frac{1} {2}$$
B.$$\frac{\sqrt2} {2}$$
C.$${\sqrt {3}}$$
D.$$\frac{\sqrt{3}} {3}$$
6、['临界角'， '全反射定义、条件等相关概念'， '光的颜色 色散'， '折射率定义式及物理意义']正确率40.0%如图所示，一细束白光通过玻璃三棱镜折射后分为各种单色光，取其中$$a， ~ b， ~ c$$三种色光，下列说法正确的是$${{(}{)}}$$
A
A.玻璃三棱镜对$${{c}}$$光的折射率最小
B.若分别让$$a， ~ b， ~ c$$三色光通过一双缝装置，则$${{a}}$$光形成的干涉条纹的间距最大。
C.$$a， ~ b， ~ c$$三色光在玻璃三棱镜中的传播速度依次越来越小
D.若让$$a， ~ b， ~ c$$三色光以同一入射角$${、}$$从空气中射入某一介质，$${{b}}$$光恰能发生全反射，则$${{c}}$$光也一定能发生全反射
7、['临界角'， '光的折射现象'， '全反射定义、条件等相关概念'， '折射率定义式及物理意义']正确率40.0%关于光的传播下列说法正确的是$${{(}{)}}$$
D
A.光是沿直线传播的，它的传播速度是$$3 \times1 0^{-8} m / s$$
B.光射到两种介质的界面上一定同时发生光的反射和折射现象
C.光射到两种介质的界面上，如果入射角大于临界角就发生全反射
D.介质对真空的折射率一定大于$${{1}}$$
8、['折射率定义式及物理意义'， '折射定律的内容及表达式']正确率40.0%以往，已知材料的折射率都为正值$$( n > 0 )$$．现已有针对某些电磁波设计制作的人工材料，其折射率可以为负值$$( \boldsymbol{n} < \mathbf{0} )$$，成为负折射率材料．位于空气中的这类材料，入射角$${{i}}$$与折射角$${{r}}$$依然满足$$\frac{\operatorname{s i n} i} {\operatorname{s i n} r}=n，$$但是折射线与入射线位于法线的同一侧（此时折射角取负值）．若该材料对电磁波的折射率$${{n}{=}{−}{1}}$$，则从空气中一点光源发射的光线射向这种材料的光路图是（）
C
A.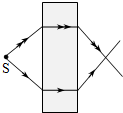
B.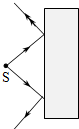
C.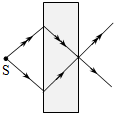
D.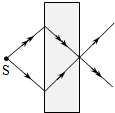
正确率40.0%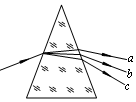
如图所示，一束平行光经玻璃三棱镜折射后分解为互相分离的$$a， ~ b， ~ c$$
C
A.当它们在真空中传播时，$${{c}}$$光的波长最大
B.当它们在玻璃中传播时，$${{c}}$$光的速度最大
C.若它们都从玻璃射向空气，$${{c}}$$光发生全反射的临界角最小
D.对同一双缝干涉装置，$${{a}}$$光干涉条纹之间的距离最小
10、['全反射定义、条件等相关概念'， '光导纤维'， '折射率定义式及物理意义']正确率40.0%
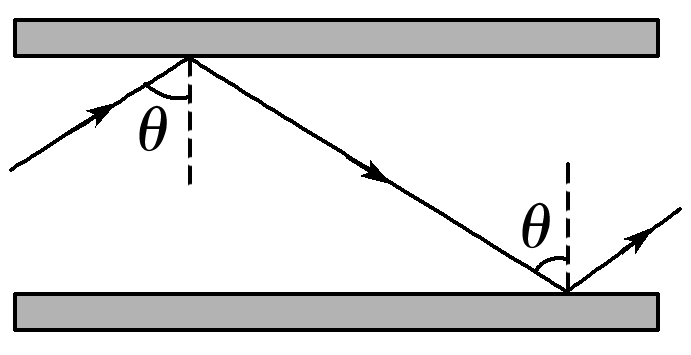
如图所示是两个城市间光缆中的一条光导纤维的一段，光缆总长为 $${{L}}$$ ，它的玻璃芯的折射率为 $${{n}_{1}}$$ ，外层材料的折射率为 $${{n}_{2}{.}}$$ 若光在空气中的传播速度近似为 $${{c}}$$ ，则对于光由它的一端射入经多次全反射后从另一端射出的过程，下列判断中正确的是 $${{(}{)}}$$
D
A.$${{n}_{1}{<}{{n}_{2}}}$$，光通过光缆的时间等于$$\frac{n_{1} L} {c}$$
B.$${{n}_{1}{<}{{n}_{2}}}$$，光通过光缆的时间大于$$\frac{n_{1} L} {c}$$
C.$${{n}_{1}{>}{{n}_{2}}}$$，光通过光缆的时间等于$$\frac{n_{1} L} {c}$$
D.$${{n}_{1}{>}{{n}_{2}}}$$，光通过光缆的时间大于$$\frac{n_{1} L} {c}$$
1. 题目未给出完整信息，无法直接解析。通常涉及光的传播时间与折射率的关系，但缺少关键条件（如折射率或光速）。
2. 根据折射现象，频率越高折射率越大，因此： $$n_a < n_b \Rightarrow \nu_a < \nu_b$$（B正确）。 全反射临界角 $$C = \arcsin(1/n)$$，折射率越大临界角越小，故a光先消失（D正确）。 传播时间 $$t = \frac{d}{v} = \frac{dn}{c}$$，折射率越小时间越短，a光时间更短（C正确）。 综上，A错误，B、C、D正确。
3. 蓝光折射率大于红光，经过半圆形玻璃砖后蓝光偏折更明显，因此P为红光，Q为蓝光。选项B（P为红光）和C（Q为蓝光）正确。
4. 折射率关系：$$n_{\text{红}} < n_{\text{绿}}$$。视深公式 $$d' = \frac{d}{n}$$，折射率越大看起来越浅，因此绿灯看起来较浅（C正确）。
5. 光线垂直AB入射，进入棱镜后方向不变。在AC面入射角为30°，折射角为60°（因出射光线与AC夹角为30°）。由折射定律： $$n = \frac{\sin 60°}{\sin 30°} = \sqrt{3}$$（C正确）。
6. 白光色散中偏折角越大折射率越大，假设a光偏折最小、c光最大，则： - 折射率 $$n_a < n_b < n_c$$（A错误）。 - 波长 $$\lambda_a > \lambda_b > \lambda_c$$，干涉条纹间距 $$\Delta x \propto \lambda$$，a光间距最大（B正确）。 - 速度 $$v = c/n$$，a光速度最大（C错误）。 - 全反射临界角 $$C = \arcsin(1/n)$$，c光临界角最小，若b光恰能全反射，c光一定能（D正确）。 综上，B、D正确。
7. 光在介质中可能发生全反射（C正确），且介质折射率 $$n > 1$$（D正确）。光速 $$3 \times 10^8 \, \text{m/s}$$ 是真空中速度（A错误），界面反射和折射不一定同时发生（B错误）。
8. 负折射率 $$n=-1$$ 时，折射线与入射线在法线同侧且对称。选项中C符合此特征。
9. 假设a光偏折最大、c光最小，则折射率 $$n_a > n_b > n_c$$，因此： - 真空中波长 $$\lambda_c$$ 最大（A正确）。 - 玻璃中速度 $$v_c$$ 最大（B正确）。 - 全反射临界角 $$C_c$$ 最大（C错误）。 - 干涉条纹间距 $$\Delta x \propto \lambda$$，a光最小（D正确）。 综上，A、B、D正确。
10. 光导纤维要求 $$n_1 > n_2$$ 以实现全反射。光程 $$s = \frac{L}{\sin \theta}$$，传播时间 $$t = \frac{s}{v} = \frac{n_1 s}{c} > \frac{n_1 L}{c}$$（D正确）。