.jpg)
正确率40.0%如图所示，两束光线甲和乙分别射到同一双缝干涉装置得到的干涉图样如图甲、乙所示，将这两束光以不同的角度同时沿不同的半径方向射入同一块横截面为半圆形的玻璃柱体，其透射光线都是由圆心$${{O}}$$点沿$${{O}{C}}$$方向射出，下列说法正确的是$${{(}{)}}$$
A.甲光的频率较低，乙光的频率较高
B.$${{A}}$$光与甲光对应，$${{B}}$$光与乙光对应
C.分别让$${{A}}$$、$${{B}}$$光通过同一单缝，在同一光屏上$${{A}}$$光的条纹宽度大于$${{B}}$$光的条纹宽度
D.$${{A}}$$光在玻璃中传播速度大，$${{B}}$$光在玻璃中传播速度小
2、['全反射'， '折射定律的内容及表达式']正确率40.0%“道威棱镜”广泛地应用在光学仪器中，如图所示，将一等腰直角棱镜截去棱角，使其平行于底面，可制成“道威棱镜”，这样就减小了棱镜的重量和杂散的内部反射。一束由红绿两色组成的复色光从$${{A}{B}}$$边中点$${{E}}$$平行于$${{B}{C}}$$边射入，红光在$${{B}{C}}$$边发生全反射后再从$${{C}{D}}$$边的中点$${{F}}$$射出玻璃砖。则下列说法正确的是$${{(}{)}}$$
A.绿光第一次入射到$${{B}{C}}$$边一定会发生全反射
B.绿光第一次从$${{C}{D}}$$边的出射点在$${{F}}$$点的下方
C.绿光在玻璃砖内传播的速度比红光快
D.红绿光第一次从$${{C}{D}}$$边出来的折射光都与$${{B}{C}}$$边平行
3、['折射定律的内容及表达式']正确率40.0%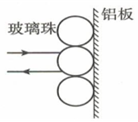
高速公路上的标志牌都使用“回归反光膜”，这种膜是用球体反射元件制成的。如图所示，反光膜内均匀分布着球形的细玻璃珠，所用玻璃的折射率为$${{1}{.}{6}}$$，入射的车灯光线经玻璃珠折射$${{→}}$$反射$${{→}}$$折射后恰好和入射光线平行，则光进入玻璃珠后的折射角的正弦值为$${{(}{)}}$$
C
A.$${{0}{.}{9}{6}}$$
B.$${{0}{.}{8}}$$
C.$${{0}{.}{6}}$$
D.$${{0}{.}{3}}$$
4、['折射定律与全反射综合'， '全反射定义、条件等相关概念'， '折射定律的内容及表达式']正确率40.0%如图所示为某半圆柱体玻璃砖的横截面，$${{B}{C}}$$为直径，一束由$${{a}}$$光和$${{b}}$$光组成的复色光沿$${{A}{B}}$$方向由真空从$${{B}{C}}$$面射入玻璃砖，之后分成两束分别从$${{D}}$$、$${{E}}$$两点射出$${{(}}$$不考虑光在玻璃砖中的反射$${{)}}$$。已知该玻璃砖对$${{a}}$$光的折射率大于对$${{b}}$$光的折射率，则下列说法正确的是$${{(}{)}}$$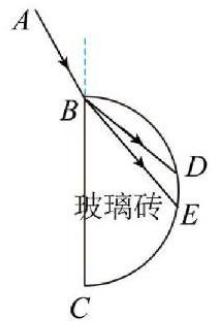
B
A.$${{a}}$$光和$${{b}}$$光在玻璃砖中的传播速度相等
B.$${{a}}$$光和$${{b}}$$光在玻璃砖中的传播时间相等
C.从$${{D}}$$点射出的为$${{b}}$$光，从$${{E}}$$点射出的为$${{a}}$$光
D.若从水中射入空气时，$${{a}}$$光发生全反射的临界角更大
5、['全反射'， '光导纤维'， '折射定律的内容及表达式']正确率40.0%
光纤已经普遍应用到了通信领域，具有可弯曲、传输速度快、信息量大的优点．将一段光纤材料弯曲成四分之一圆弧，一束激光沿如图所示方向垂直射入材料一端，已知光纤材料的直径为$${{2}{c}{m}}$$，该激光在光纤材料中的折射率$${{n}{=}{{1}{.}{5}{.}}}$$若光束从入射端传至另一端的过程中不能沿侧壁射出，则弯曲光纤材料时对应的最小半径$${{R}}$$为$${{(}{)}}$$
B
A.$${{2}{c}{m}}$$
B.$${{4}{c}{m}}$$
C.$${{6}{c}{m}}$$
D.$${{8}{c}{m}}$$
6、['光的折射现象'， '折射定律的内容及表达式']正确率40.0%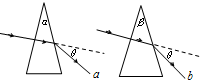
如图所示，有$${{a}{、}{b}}$$
B
A.$${{a}}$$是红光，$${{b}}$$是紫光
B.$${{a}}$$是紫光，$${{b}}$$是红光
C.可能$${{a}{、}{b}}$$都是红光
D.可能$${{a}{、}{b}}$$都是紫光
7、['临界角'， '双缝干涉现象及条件'， '光的偏振现象及应用'， '折射率定义式及物理意义'， '折射定律的内容及表达式']正确率40.0%两种单色光分别通过同一双缝干涉装置得到的干涉图样如图甲$${、}$$乙所示．图丙中有一半圆玻璃砖，$${{O}}$$是圆心，$${{M}{N}}$$是法线，$${{P}{Q}}$$是足够长的光屏．甲单色光以入射角$${{i}}$$由玻璃砖内部射向$${{O}}$$点，折射角为$${{r}}$$.则下列说法正确的是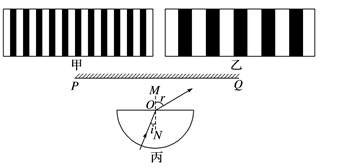
D
A.乙光以$${{i}}$$入射时一定发生全反射
B.甲光的频率比乙光的频率小
C.光的干涉现象说明光是一列横波
D.甲光在玻璃砖中的临界角$${{C}}$$满足$$\operatorname{s i n} \， C=\frac{\operatorname{s i n} i} {\operatorname{s i n} r}$$
8、['全反射定义、条件等相关概念'， '折射定律的内容及表达式']正确率40.0%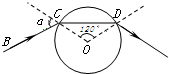
如图所示，真空中有一个半径为$${{R}}$$，质量分布均匀的玻璃球，频率为$${{γ}}$$的细光束的真空中沿直线$${{B}{C}}$$传播，并于玻璃球表面的$${{C}}$$点经折射进入玻璃球，并在玻璃球表面的$${{D}}$$点又经折射进入真空中，已知$$\angle C O D=1 2 0^{\circ}$$，玻璃球对该激光的折射率为$${\sqrt {3}}$$，则下列说法中正确的是$${{(}{)}}$$
C
A.一个光子在穿过玻璃球的过程中能量逐渐变小
B.改变入射角$${{α}}$$的大小，细激光束可能在玻璃球的内表面发生全反射
C.此激光束在玻璃中穿越的时间为$$t=3 R / c ( c$$为真空中的光速$${{)}}$$
D.激光束的入射角为$${{α}{=}{{4}{5}}{°}}$$
9、['光的折射现象'， '折射定律的内容及表达式']正确率40.0%
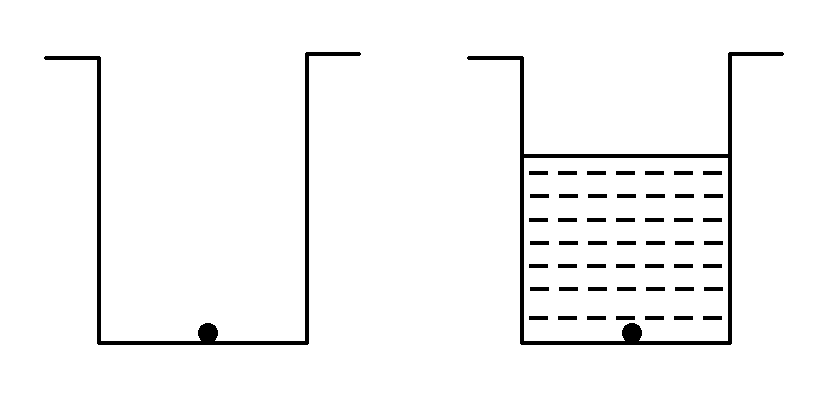
如图所示，井口大小和深度相同的两口井，一口是枯井，一口是水井 $${{(}}$$ 水面在井口之下 $${{)}}$$ ，两井底部各有一只青蛙，则 $${{(}{)}}$$
B
A.水井中的青蛙觉得井口大些，晴天的夜晚，水井中的青蛙能看到更多的星星
B.枯井中的青蛙觉得井口大些，晴天的夜晚，水井中的青蛙能看到更多的星星
C.水井中的青蛙觉得井口小些，晴天的夜晚，枯井中的青蛙能看到更多的星星
D.两只青蛙觉得井口一样大，晴天的夜晚，水井中的青蛙能看到更多的星星
10、['光的折射现象'， '折射定律的内容及表达式']正确率40.0%以往，已知材料的折射率都为正值$$( n > 0 ).$$现已有针对某些电磁波设计制作的人工材料，其折射率可以为负值$$( n < 0 )$$，成为负折射率材料．位于空气中的这类材料，入射角$${{i}}$$与折射角$${{r}}$$依然满足$$\frac{\operatorname{s i n} i} {\operatorname{s i n} r}=n$$，但是折射线与入射线位于法线的同一侧$${{(}}$$此时折射角取负值$${{)}{.}}$$若该材料对电磁波的折射率$${{n}{=}{−}{1}}$$，则从空气中一点光源发射的光线射向这种材料的光路图是$${{(}{)}}$$
C
A.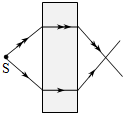
B.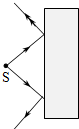
C.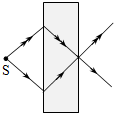
D.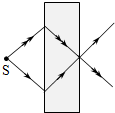
1. 解析：
根据双缝干涉图样，甲光的条纹间距大于乙光，说明甲光的波长较长，频率较低（$$λ = \frac{dΔx}{L}$$，$$v = \frac{c}{λ}$$）。由于两束光在玻璃柱体中折射后均沿$$OC$$方向射出，说明入射角相同，但折射率不同。频率高的光（乙光）折射率更大（$$n = \frac{c}{v}$$），因此$$B$$光（折射率大）对应乙光，$$A$$光对应甲光。$$A$$光频率低，在玻璃中传播速度更大（$$v = \frac{c}{n}$$），且通过单缝时衍射条纹更宽（$$Δx ∝ λ$$）。综上，选项C、D正确。
2. 解析：
绿光频率高于红光，折射率更大（$$n_{绿} > n_{红}$$），临界角更小（$$C = \arcsin(1/n)$$）。红光已在$$BC$$边全反射，绿光必然全反射（A正确）。绿光折射率大，偏折更明显，出射点$$F$$下方（B正确）。绿光在玻璃中速度更慢（$$v = c/n$$，C错误）。由几何关系，红绿光出射时均平行于$$BC$$（D正确）。故选A、B、D。
3. 解析：
光线经玻璃珠折射→反射→折射后与入射光线平行，说明反射时光路对称。设入射角为$$i$$，折射角为$$γ$$，由折射定律$$n\sinγ = \sin i$$。反射后出射角为$$i$$，根据几何关系，两次折射后光线平行要求$$2γ = 180° - i$$。联立解得$$\sinγ = 0.6$$（$$n=1.6$$时，$$i≈53°$$，$$γ≈30°$$）。故选C。
4. 解析：
玻璃砖对$$a$$光折射率更大（$$n_a > n_b$$），因此$$a$$光传播速度更小（$$v = c/n$$，A错误）。由于$$a$$光折射率大，偏折更明显，从$$E$$点射出（C错误）。若路径长度相同，$$a$$光传播时间更长（$$t = \frac{L}{v}$$），但图中$$a$$光路径更短，时间可能相等（B可能正确）。$$a$$光临界角更小（$$C = \arcsin(1/n)$$，D错误）。故选B。
5. 解析：
激光在光纤中全反射的临界角为$$θ_c = \arcsin(1/n) ≈ 41.8°$$。为使光不侧壁射出，弯曲半径需满足$$R ≥ \frac{d/2}{1 - \cosθ_c}$$，代入$$d=2\,\text{cm}$$得$$R ≥ 4\,\text{cm}$$。故选B。
6. 解析：
图中未提供具体信息，但若$$a$$、$$b$$为不同色光，紫光折射率大，偏折更明显（$$n_{紫} > n_{红}$$）。若均为同种光，则可能为同一频率。需根据题目补充内容判断，但选项B（$$a$$为紫光，$$b$$为红光）是常见情况。
7. 解析：
甲光条纹间距大，波长长，频率低（B正确）。乙光频率高，折射率大，临界角小，但全反射需满足$$i ≥ C$$，题目未给出具体角度（A不确定）。干涉现象与横波/纵波无关（C错误）。临界角公式为$$\sin C = 1/n$$，而$$n = \sin i / \sin r$$，故D正确。故选B、D。
8. 解析：
光子能量不变（A错误）。玻璃球内表面不可能全反射，因折射角小于临界角（B错误）。光在玻璃中路径长度$$L = 2R\cos30° = \sqrt{3}R$$，时间$$t = \frac{L}{v} = \frac{\sqrt{3}R}{c/\sqrt{3}} = 3R/c$$（C正确）。由折射定律$$\sinα = n\sin(30°)$$，得$$α = 60°$$（D错误）。故选C。
9. 解析：
水井中光线折射使青蛙视角变大，觉得井口更大，且能看到更多星星（A正确）。枯井中无折射，视角较小。
10. 解析：
负折射率$$n=-1$$时，折射线与入射线在法线同侧，且$$r = -i$$（满足$$\sin i / \sin r = -1$$）。光路图应显示入射与折射光线对称于界面，且方向相反。故选C。