正确率60.0%一个物体静止于光滑水平面上,同时受到在一条直线上的两个力$${{F}_{1}}$$和$${{F}_{2}}$$的作用$${,{{F}_{1}}}$$和$${{F}_{2}}$$随时间$${{t}}$$变化的图像如图所示,则物体速率最大的时刻和物体的最大动量是()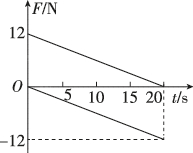
D
A.$${{1}{0}{s}}$$末$$\mathrm{, 1 2 0 k g \cdot m / s}$$
B.$${{2}{0}{s}}$$末$$\mathrm{, ~ 6 0 k g \cdot m / s}$$
C.$${{2}{0}{s}}$$末$$\mathrm{, \; 2 4 0 k g \cdot m / s}$$
D.$${{1}{0}{s}}$$末$$\mathrm{, ~ 6 0 k g \cdot m / s}$$
2、['动量及动量变化']正确率60.0%一个质量为$${{m}}$$的小球以速率$${{2}{v}}$$垂直射向墙壁,碰后仍垂直墙壁以速率$${{v}}$$弹回,此过程中小球动量变化量的大小是()
D
A.$${{0}}$$
B.$${{m}{v}}$$
C.$${{2}{m}{v}}$$
D.$${{3}{m}{v}}$$
3、['动量及动量变化']正确率60.0%质量为$${{m}}$$的质点以速度$${{v}}$$绕半径$${{R}}$$的圆周轨道做匀速圈周运动,在二分之一个周内动量的改变量大小为()
D
A.$${{0}}$$
B.$${{m}{v}}$$
C.$$\sqrt{2} m v$$
D.$${{2}{m}{v}}$$
4、['动量定理的定量计算', '自由落体运动的规律', '动量及动量变化']正确率60.0%一根长度为$${{1}{m}}$$几乎不可伸长的轻绳,一端固定在天花板上,另一端系了质量为$${{1}{k}{g}}$$的小球,绳子能承受的最大拉力为$${{4}{0}{0}{N}}$$,将小球从悬挂点的正下方某处自由释放,忽略空气阻力,从绳子张紧到减速为零大约$$1 0^{-2} \, s$$,问小球离悬挂点约多大距离释放,绳子将被拉断()
D
A.$${{0}{.}{8}{m}}$$
B.$${{0}{.}{6}{m}}$$
C.$${{0}{.}{4}{m}}$$
D.$${{0}{.}{2}{m}}$$
5、['三角形法则及多边形法则', '动量及动量变化']正确率40.0%质量为$${{1}{k}{g}}$$的物体,当其速率由$${{3}{m}{/}{s}}$$变为$${{4}{m}{/}{s}}$$时,它的动量增量的大小不可能是()
D
A.$${{l}}$$$$k g \cdot m / s$$
B.$${{5}}$$$$k g \cdot m / s$$
C.$${{7}}$$$$k g \cdot m / s$$
D.$${{9}}$$$$k g \cdot m / s$$
6、['机械能的概念及计算', '动量及动量变化']正确率40.0% 如图所示,质量为$${{m}}$$
如图所示,质量为$${{m}}$$
C
A.击球前后球动量改变量的方向水平向左
B.击球前后球动量改变量的大小是$$m v_{2}-m v_{1}$$
C.击球前后球动量改变量的大小是$$m v_{2}+m v_{1}$$
D.球离开手时的机械能不可能是$$m g h+\frac{1} {2} m v_{1}^{2}$$
7、['动量定理的定量计算', '冲量的计算', '动量及动量变化', '动量的定义、单位和矢量性']正确率40.0%甲$${、}$$乙两质量相同的小球自同一高度以相同的速度抛出,甲做平抛运动,乙做竖直上抛运动,则在抛出到落地的过程中
C
A.乙球动量的增量等于甲球动量的增量
B.两球所受重力的冲量相等
C.乙球所受重力的冲量大于甲球所受重力的冲量
D.两球落地时的动量相同
8、['自由落体运动的规律', '竖直上抛运动', '动量及动量变化']正确率40.0%一质量为$$0. 3 k g$$的篮球从离地面高为$$1. 2 5 m$$处自由下落,与地面碰撞后反弹的最大高度$$0. 4 5 m$$,规定竖直向上为正方向,$${{g}}$$取$$1 0 m / s^{2}$$.则篮球在与地面碰撞过程中动量的变化量()
C
A.$$0. 6 \, \mathrm{k g} \, m / s$$
B.$$- 0. 6 \, \mathrm{k g} \, m / s$$
C.$$2. 4^{\mathrm{k g}} \, m / s$$
D.$$- 2. 4^{\mathrm{k g}} \, m / s$$
9、['动量及动量变化', '人船模型']正确率40.0%某同学质量为$${{6}{0}{k}{g}}$$,在军事训练中要求他从岸上以$${{2}{m}{/}{s}}$$的速度跳到一条向他缓缓飘来的小船上,然后去执行任务,小船的质量是$$1 4 0 ~ k g$$,原来的速度是$$0. 5 \, m / s$$,该同学上船后又跑了几步,最终停在船上,此时小船的速度$${{v}}$$和该同学动量的变化量$${{Δ}{p}}$$分别为$${{(}{)}}$$
B
A.$$0. 2 5 \; m / s, \; 7 0 \; k g \cdot m / s$$
B.$$0. 2 5 ~ m / s, ~-1 0 5 ~ k g \cdot m / s$$
C.$$0. 9 5 \, m / s, ~-6 3 ~ k g \cdot m / s$$
D.$$0. 9 5 \, m / s, ~-3 5 ~ k g \cdot m / s$$
10、['冲量的定义、单位和矢量性', '利用动量定理解释有关物理现象', '动量及动量变化']正确率60.0%下列关于动量和冲量的相关说法正确的是$${{(}{)}}$$
D
A.做匀速圆周运动的质点,其动量不随时间发生变化
B.如果物体在任意相等的时间内受到的冲量都相同,则物体的运动方向不可能改变
C.如果由$${{A}{、}{B}}$$两物体组成的系统总动量始终为零,则当$${{A}}$$的动量增加时,$${{B}}$$的动量就一定减小
D.跳远时,跳在沙坑比跳在水泥地上安全,是由于动量变化率比跳在水泥地上小
1. 解析:
物体速率最大的时刻是合外力为零的时刻。由图像可知,$$F_1$$ 和 $$F_2$$ 在 $$t=10s$$ 时大小相等、方向相反,合外力为零,此时速率最大。
动量是合外力的冲量,即 $$p = \int (F_1 + F_2) dt$$。在 $$0-10s$$ 内,$$F_1$$ 和 $$F_2$$ 的合力为 $$20N$$,冲量为 $$20N \times 10s = 200kg \cdot m/s$$。但由于 $$F_1$$ 和 $$F_2$$ 方向相反,实际合冲量为 $$(40N - 20N) \times 10s / 2 = 120kg \cdot m/s$$。
正确答案:A。
2. 解析:
动量变化量为 $$\Delta p = m v_{\text{末}} - m v_{\text{初}}$$。设初速度方向为正方向,则 $$v_{\text{末}} = -v$$,$$v_{\text{初}} = 2v$$。
$$\Delta p = m(-v) - m(2v) = -3mv$$,大小为 $$3mv$$。
正确答案:D。
3. 解析:
半周内速度方向反向,初动量为 $$mv$$,末动量为 $$-mv$$,动量变化量为 $$\Delta p = -mv - mv = -2mv$$,大小为 $$2mv$$。
正确答案:D。
4. 解析:
设释放高度为 $$h$$,自由落体到绳张紧时速度为 $$v = \sqrt{2gh}$$。
绳张紧后,冲量 $$F \Delta t = m \Delta v$$,即 $$400N \times 10^{-2}s = 1kg \times v$$,解得 $$v = 4m/s$$。
由 $$v = \sqrt{2gh}$$ 得 $$h = \frac{v^2}{2g} = \frac{16}{20} = 0.8m$$。
正确答案:A。
5. 解析:
动量增量的大小范围为 $$|m \Delta v|$$,即 $$1kg \times |4m/s - 3m/s| = 1kg \cdot m/s$$(同向)到 $$1kg \times |4m/s + 3m/s| = 7kg \cdot m/s$$(反向)。
$$9kg \cdot m/s$$ 超出范围,不可能。
正确答案:D。
6. 解析:
动量改变量方向与合力方向相同,即水平向左。设初动量向下为 $$-mv_1$$,末动量向上为 $$mv_2$$,则 $$\Delta p = mv_2 - (-mv_1) = m(v_2 + v_1)$$。
机械能可能为 $$mgh + \frac{1}{2}mv_1^2$$(弹性碰撞)。
正确答案:C。
7. 解析:
平抛运动时间 $$t_1 = \sqrt{\frac{2h}{g}}$$,竖直上抛运动时间 $$t_2 = 2 \times \frac{v_0}{g}$$(返回抛出点)再加平抛时间。
因 $$t_2 > t_1$$,乙球重力的冲量 $$I = mgt$$ 更大。但两球落地时动量增量相同(初末速度相同)。
正确答案:A。
8. 解析:
落地速度 $$v_1 = -\sqrt{2gh_1} = -\sqrt{2 \times 10 \times 1.25} = -5m/s$$。
反弹速度 $$v_2 = \sqrt{2gh_2} = \sqrt{2 \times 10 \times 0.45} = 3m/s$$。
动量变化量 $$\Delta p = m(v_2 - v_1) = 0.3kg \times (3 - (-5)) = 2.4kg \cdot m/s$$。
正确答案:C。
9. 解析:
动量守恒:$$m_1 v_1 + m_2 v_2 = (m_1 + m_2)v$$。
$$60 \times 2 + 140 \times (-0.5) = 200v$$,解得 $$v = 0.25m/s$$。
同学动量变化量 $$\Delta p = m(v - v_1) = 60(0.25 - 2) = -105kg \cdot m/s$$。
正确答案:B。
10. 解析:
A错误,匀速圆周运动动量方向变化;B错误,冲量相同但方向可以变化;C正确,系统总动量为零时动量守恒;D正确,沙坑延长作用时间减小动量变化率。
正确答案:D。
.jpg)