.jpg)
正确率40.0%质量为$${{1}{k}{g}}$$的物体，当其速率由$${{3}{m}{/}{s}}$$变为$${{4}{m}{/}{s}}$$时，它的动量增量的大小不可能是（）
D
A.$${{l}}$$$$k g \cdot m / s$$
B.$${{5}}$$$$k g \cdot m / s$$
C.$${{7}}$$$$k g \cdot m / s$$
D.$${{9}}$$$$k g \cdot m / s$$
2、['功能关系的应用'， '动量及动量变化'， '能量守恒定律']正确率40.0%一颗子弹沿水平方向射向一个木块，第一次木块被固定在水平地面上，第二次木块静止放在光滑的水平面上，两次子弹都能射穿木块而继续飞行。这两次相比较（）
B
A.第一次子弹的动量变化较大
B.第二次子弹的动量变化较大
C.两次子弹的动量变化相等
D.无法比较两次子弹的动量变化大小
3、['平抛运动基本规律及推论的应用'， '功率的概念、计算'， '动量及动量变化']正确率40.0%如图所示，$$A. ~ B. ~ C$$是三级台阶的端点位置，每一级台阶的水平宽度是相同的，其竖直高度分别为$$h_{1} \，， \， h_{2} \，， \， h_{3}$$，将三个相同的小球分别从$$A. ~ B. ~ C$$三点以相同的速度$${{v}_{0}}$$水平抛出，最终都能到达$${{A}}$$的下一级台阶的端点$${{P}}$$处，不计空气阻力。关于从$$A. ~ B. ~ C$$三点抛出的小球，下列说法正确的是（）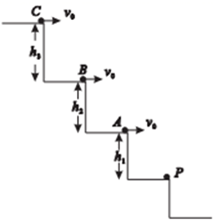
C
A.在空中运动时间之比为$$t_{A} \colon t_{B} \colon t_{C}=1 \colon\; 3 \colon\; 5$$
B.竖直高度之比为$$h_{1} \colon~ h_{2} \colon~ h_{3}=1 \colon~ 2 \colon~ 3$$
C.在空中运动过程中，动量变化率之比为$$\frac{\triangle P_{A}} {\triangle t}， \， \， \， \frac{\triangle P_{B}} {\triangle t}， \， \， \， \frac{\triangle P_{C}} {\triangle t}=1 : \， \， 1 :$$
D.到达$${{P}}$$点时，重力做功的功率之比为$$P_{A} \colon~ P_{B} \colon~ P_{C}=1 \colon~ 4 \colon~ 9$$
4、['动量及动量变化'， '人船模型']正确率40.0%某同学质量为$${{6}{0}{k}{g}}$$，在军事训练中要求他从岸上以$${{2}{m}{/}{s}}$$的速度跳到一条向他缓缓飘来的小船上，然后去执行任务，小船的质量是$$1 4 0 ~ k g$$，原来的速度是$$0. 5 \， m / s$$，该同学上船后又跑了几步，最终停在船上，此时小船的速度$${{v}}$$和该同学动量的变化量$${{Δ}{p}}$$分别为$${{(}{)}}$$
B
A.$$0. 2 5 \; m / s， \; 7 0 \; k g \cdot m / s$$
B.$$0. 2 5 ~ m / s， ~-1 0 5 ~ k g \cdot m / s$$
C.$$0. 9 5 \， m / s， ~-6 3 ~ k g \cdot m / s$$
D.$$0. 9 5 \， m / s， ~-3 5 ~ k g \cdot m / s$$
5、['动量定理的内容及表达式'， '冲量的定义、单位和矢量性'， '动量及动量变化'， '动能定理的简单应用'， '动量的定义、单位和矢量性']正确率40.0%将两个相同的小球从同一高度以相同的速率分别平抛和斜向上抛出，不计空气阻力，则从抛出到落地的过程中（）
D
A.落地时两个小球的动量相同
B.重力对两个小球的冲量相同
C.两个小球动量的变化量相同
D.两个小球动能的变化量相同
6、['冲量的定义、单位和矢量性'， '冲量、动量和动能的区别及联系'， '动量及动量变化'， '动量的定义、单位和矢量性']正确率40.0%关于动量和冲量，下列说法正确的是$${{(}{)}}$$
A
A.对于某物体而言，动量越大，其速度一定越大
B.力越大，力的冲量就越大
C.物体动量的方向一定与其所受合力的方向一致
D.若两个力的大小相等，作用时间也相同，则这两个力的冲量一定相同
7、['动量定理的内容及表达式'， '冲量的计算'， '平衡状态的定义及条件'， '动量及动量变化']正确率40.0%一质量为$${{m}}$$的物体沿倾角为$${{θ}}$$的固定斜面匀速下滑，在下滑时间$${{t}}$$内，斜面对物体作用力的冲量为（）
B
A.方向垂直斜面向上
B.方向竖直向上
C.大小等于$$m g t \operatorname{c o s} \theta$$
D.大小等于$$m g t \operatorname{s i n} \theta$$
8、['计算物体动能的变化'， '动量及动量变化']正确率40.0%一只小球沿光滑水平面运动，垂直撞到竖直墙上．小球撞墙前后的动量变化量为$${{△}{P}}$$，动能变化量为$${{△}{E}}$$，下列关于$${{△}{P}}$$和$${{△}{E}}$$说法中正确的是$${{(}{)}}$$
B
A.若$${{△}{P}}$$最大，则$${{△}{E}}$$也最大
B.若$${{△}{P}}$$最大，则$${{△}{E}}$$一定最小
C.若$${{△}{P}}$$最小，则$${{△}{E}}$$也最小
D.若$${{△}{P}}$$最小，则$${{△}{E}}$$一定最小
9、['动量定理的定量计算'， '冲量的计算'， '功率和速度的关系'， '从受力确定运动情况'， '动量及动量变化'， '动量的定义、单位和矢量性']正确率40.0%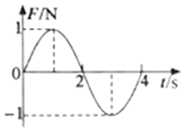
一质点静止在光滑水平面上，现对其施加水平外力$${{F}{，}{F}}$$
D
A.第$${{2}{s}}$$末，质点的动量为$${{0}}$$
B.第$${{2}{s}}$$末，质点距离出发点最远
C.在$${{0}{～}{2}{s}}$$内，$${{F}}$$的功率一直增大
D.在$${{0}{～}{4}{s}}$$内，$${{F}}$$的冲量为$${{0}}$$
10、['动量及动量变化'， '动能定理的简单应用']正确率40.0%$${{2}{0}{1}{8}}$$年$${{1}}$$月$${{1}{1}}$$日，福建省高校首支女子手球队在莆田学院成立。女子手球比赛采用的是质量$$m=0. 4 k g$$的$${{2}}$$号球，若$${{2}}$$号手球竖直向下以$${{5}{m}{/}{s}}$$的速度落至水平地面，再以$${{3}{m}{/}{s}}$$的速度反向弹回。取竖直向上为正方向，在小球与地面接触的时间内，关于球的动量的变化量$${{△}{p}}$$和合外力对小球做的功，下列结果正确的是（）
D
A.$$W=-6. 8 J， \， \， \， \triangle p=0. 8 k g \cdot m / s$$
B.$$W=-3. 2 J， \， \， \， \triangle p=0. 8 k g \cdot m / s$$
C.$$W=-6. 8 J， \， \， \， \triangle p=3. 2 k g \cdot m / s$$
D.$$W=-3. 2 J， \， \， \， \triangle p=3. 2 k g \cdot m / s$$
1. 动量增量的大小可以通过初始和末态动量的矢量差计算。初始动量 $$p_1 = 1 \times 3 = 3 \, \text{kg} \cdot \text{m/s}$$，末态动量 $$p_2 = 1 \times 4 = 4 \, \text{kg} \cdot \text{m/s}$$。由于速度方向未知，动量增量的大小范围为 $$|p_2 - p_1| \leq \Delta p \leq p_2 + p_1$$，即 $$1 \leq \Delta p \leq 7$$。因此，$$9 \, \text{kg} \cdot \text{m/s}$$ 不可能，选 D。
3. 小球水平抛出后，运动时间由竖直高度决定，$$t = \sqrt{\frac{2h}{g}}$$，由于 $$h_1, h_2, h_3$$ 的比例关系未给出，无法直接比较时间比。动量变化率 $$\frac{\Delta P}{\Delta t} = mg$$，与时间无关，故比值为 $$1:1:1$$，选 C。
5. 平抛和斜抛小球落地时速度方向不同，动量不同；但重力冲量 $$I = mgt$$，时间相同，冲量相同；动量变化量 $$\Delta p = mgt$$ 也相同；动能变化量由高度决定，相同。选 B、C、D。
7. 物体匀速下滑，斜面对其作用力为支持力和摩擦力的合力，方向竖直向上，大小等于重力 $$mg$$。冲量大小为 $$mgt$$，方向竖直向上，选 B。
9. 由 $$F-t$$ 图可知，$$0-2s$$ 内 $$F$$ 的冲量为 $$0$$，质点动量不变，$$2s$$ 末动量为 $$0$$，且位移最大。$$0-2s$$ 内 $$F$$ 先正后负，功率先增后减。$$0-4s$$ 内 $$F$$ 的冲量为 $$0$$。选 A、B、D。