正确率19.999999999999996%某同学利用所学知识测水龙头水流对地面的冲击速度,水的流量是$$Q=9 \times1 0^{-4} m^{3} / \mathrm{s}$$.现将质量为$${{0}{.}{5}{{k}{g}}}$$的杯子放在台秤上,水龙头开始往杯中注水,开始注水至$${{1}{0}{s}}$$末时,台秤的读数为$$9 8. 6 \mathrm{N}$$.假设水流垂直打在杯子底面后没有反弹,水的密度$$\rho=1 \times1 0^{3} \mathrm{k g} / m^{3}, \, \, \, g$$取$${{1}{0}{{m}{/}{s}^{2}}}$$.则注入杯中水流的速率约为()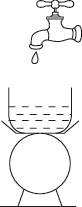
B
A.$${{3}{{m}{/}{s}}}$$
B.$${{4}{{m}{/}{s}}}$$
C.$${{5}{{m}{/}{s}}}$$
D.$${{6}{{m}{/}{s}}}$$
2、['利用动量定理处理流体变动问题', '牛顿第三定律的内容及理解']正确率60.0%$${{2}{0}{2}{0}}$$年新型冠状病毒主要传播方式为飞沫传播,打喷嚏可以将飞沫喷到十米之外.有关专家研究得出打喷嚏时气流喷出的速度可达$${{4}{0}{{m}{/}{s}}}$$.假设打一次喷嚏大约喷出$${{5}{0}{{m}{L}}}$$的空气,用时约$$0. 0 2 \mathrm{s},$$已知空气的密度为$$1. 3 \mathrm{k g} / \mathrm{m}^{3} \,,$$估算打一次喷嚏时人受到的平均反冲力为()
B
A.$${{1}{3}{N}}$$
B.$$0. 1 3 \mathrm{N}$$
C.$$\ 0. 6 8 \mathrm{N}$$
D.$${{2}{.}{6}{N}}$$
3、['自由落体运动的规律', 'v-t图像斜率意义,及v-t图像求加速度', '利用动量定理处理流体变动问题', 'v-t图像面积意义,及v-t图像求位移', 'v-t图像综合应用', '利用动量定理求解其他问题', '竖直上抛运动']正确率60.0%如图所示为运动传感器探测到小球由静止释放后撞击地面弹跳的$${{v}{−}{t}}$$图像,小球质量为$$0. 5 k g$$,重力加速度$$g ~=~ 1 0 m / s^{2}$$,空气阻力不计根据图像可知()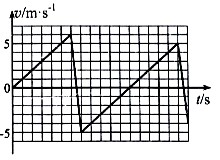
C
A.小球下落的初始位置离地面的高度为$$1. 2 5 m$$
B.小球第一次反弹的最大高度为$${{1}{.}{8}{m}}$$
C.横坐标每一小格表示的时间是$${{0}{.}{1}{s}}$$
D.小球第一次撞击地面时地面给小球的平均作用力为$${{5}{5}{N}}$$
4、['动量定理的定量计算', '利用动量定理处理流体变动问题', '利用牛顿第三定律解决问题']正确率40.0%如图所示,装有氮气的钢瓶停放在光滑的水平地面上,瓶的底端与竖直墙壁接触.现打开左端阀门,气体水平向左喷出,设喷口的面积为$${{S}}$$,气体的密度为$${{ρ}{,}}$$气体向外喷出的速度为$${{v}}$$,则$${{Δ}{t}}$$内墙壁受到的冲量为()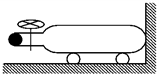
C
A.$$\rho v s \Delta t$$
B.$$\frac{\rho v^{2}} {s} \Delta t$$
C.$$\rho v^{2} s \Delta t$$
D.$${\frac{1} {2}} \rho v^{2} \, s$$
5、['利用动量定理处理流体变动问题']正确率40.0%超强台风$${{“}}$$利奇马$${{”}}$$在$${{2}{0}{1}{9}}$$年$${{8}}$$月$${{1}{0}}$$日凌晨$${{1}}$$点$${{4}{5}}$$分前后在浙江省温岭市沿海登陆,登陆时中心附近最大风力$${{1}{6}}$$级$${{(}{{5}{2}}}$$米$${{/}}$$秒$${{)}}$$,是新中国成立之后登陆我国强度第五的超强台风,风力大,降水强度大,影响范围广,涉及到$${{1}{0}}$$个省区市,持续时间长,也是历史上少有的超强台风,对固定建筑物破坏程度非常巨大。请你根据所学物理知识推算固定建筑物所受风力(空气的压力)与风速(空气流动速度)大小关系,假设某一建筑物垂直风速方向的受力面积为$${{S}}$$,风速大小为$${{v}}$$,空气吹到建筑物上后速度瞬间减为零,空气密度为$${{ρ}}$$,风力$${{F}}$$与风速大小$${{v}}$$关系式为$${{(}{)}}$$
B
A.$$F=\rho S v$$
B.$$F=\rho S v^{2}$$
C.$$F=\frac{1} {2} \rho S v^{3}$$
D.$$F=\rho S v^{3}$$
6、['利用动量定理处理流体变动问题', '牛顿第三定律的内容及理解']正确率40.0%有一宇宙飞船以$$v=1 0 k m / s$$在太空中飞行,突然进入一密度为$$\rho=1 \times1 0^{-7} k g / m^{3}$$的微陨石尘区,假设微陨石尘与飞船碰撞后即附着在飞船上.已知飞船的正横截面积$${{S}{=}{2}{{m}^{2}}}$$,欲使飞船保持原速度不变,试求飞船的助推器的助推力应增大()
A
A.$${{2}{0}{N}}$$
B.$${{3}{0}{N}}$$
C.$${{4}{0}{N}}$$
D.$${{5}{0}{N}}$$
7、['利用动量定理处理流体变动问题', '牛顿第三定律的内容及理解']正确率40.0%一辆公交车车头迎风面积为$${{S}}$$,正在逆风行驶,行驶速度为$${{v}_{1}}$$,风速为$${{v}_{2}}$$,空气密度为$${{ρ}}$$,逆风行驶时公交车受到的平均风力约为()
A
A.$$\rho S ( v_{2}+v_{1} )^{2}$$
B.$${{ρ}{S}{v}{^{2}_{1}}}$$
C.$${{ρ}{S}{v}{^{2}_{2}}}$$
D.$$\rho S ( v_{2}-v_{1} )^{2}$$
8、['利用动量定理处理流体变动问题', '利用牛顿第三定律解决问题']正确率40.0%水刀切割具有精度高$${、}$$无热变形$${、}$$无毛刺$${、}$$无需二次加工以及节约材料等特点,得到广泛应用。某水刀切割机床如图所示,若横截面直径为$${{d}}$$的水流以速度$${{v}}$$垂直射到要切割的钢板上,碰到钢板后水的速度减为零,已知水的密度为$${{ρ}{,}}$$则钢板受到水的冲力大小为
D
A.$${{π}{ρ}{{d}^{2}}{v}}$$
B.$${{π}{ρ}{{d}^{2}}{{v}^{2}}}$$
C.$${\frac{1} {4}} \pi\rho d^{2} v$$
D.$${\frac{1} {4}} \pi\rho d^{2} v^{2}$$
9、['利用动量定理处理流体变动问题']正确率40.0%高压水枪喷口半径为$${{r}}$$,射出的水流速度为$${{v}}$$,水平地打在竖直煤壁上后速度变为零。设水的密度为$${{ρ}}$$,则高速水流对煤壁冲击力的大小为$${{(}{)}}$$
C
A.$${{π}{ρ}{{r}^{2}}{v}}$$
B.$$2 \pi\rho r^{2} v$$
C.$${{π}{ρ}{{r}^{2}}{{v}^{2}}}$$
D.$$2 \pi\rho r^{2} v^{2}$$
10、['利用动量定理处理流体变动问题']正确率40.0%为估算伞面$${{(}}$$近似平面$${{)}}$$承受暴雨撞击产生的平均压强,小明在雨天将一圆柱形水杯置于露台,测得$${{0}{.}{5}}$$小时内杯中水位上升了$${{1}{8}{m}{m}}$$。查询得知,当时雨滴竖直下落速度约为$$1 0 m / s$$,据此估算该压强约为$${{(}}$$设雨滴撞击伞面后无反弹,不计雨滴重力,雨水的密度为$$1 \times1 0^{3} k g / m^{3} ) ( \textsubscript{<} )$$
A
A.$$0. 1 0 P a$$
B.$$1 8 0 P a$$
C.$$1. 0 P a$$
D.$$3 6 0 0 \, P a$$
1. 解析:
水流量 $$Q = 9 \times 10^{-4} \, \text{m}^3/\text{s}$$,10秒内注入水的体积为 $$V = Q \cdot t = 9 \times 10^{-3} \, \text{m}^3$$。水的质量 $$m = \rho V = 1 \times 10^3 \times 9 \times 10^{-3} = 9 \, \text{kg}$$。杯子质量 $$0.5 \, \text{kg}$$,总质量 $$9.5 \, \text{kg}$$,重力 $$95 \, \text{N}$$。台秤读数 $$98.6 \, \text{N}$$,说明水流的冲击力 $$F = 98.6 - 95 = 3.6 \, \text{N}$$。根据动量定理,$$F = \rho Q v$$,解得 $$v = \frac{F}{\rho Q} = \frac{3.6}{1 \times 10^3 \times 9 \times 10^{-4}} = 4 \, \text{m/s}$$。答案为 B。
2. 解析:
喷出空气的体积 $$V = 50 \, \text{mL} = 5 \times 10^{-5} \, \text{m}^3$$,质量 $$m = \rho V = 1.3 \times 5 \times 10^{-5} = 6.5 \times 10^{-5} \, \text{kg}$$。动量变化 $$\Delta p = m v = 6.5 \times 10^{-5} \times 40 = 2.6 \times 10^{-3} \, \text{kg} \cdot \text{m/s}$$。平均反冲力 $$F = \frac{\Delta p}{\Delta t} = \frac{2.6 \times 10^{-3}}{0.02} = 0.13 \, \text{N}$$。答案为 B。
3. 解析:
从 $$v-t$$ 图像可知,小球下落时间为 $$0.5 \, \text{s}$$(图像下降段),高度 $$h = \frac{1}{2} g t^2 = 1.25 \, \text{m}$$(A正确)。第一次反弹的最大高度对应速度由 $$4 \, \text{m/s}$$ 减为 $$0$$,时间为 $$0.4 \, \text{s}$$,高度 $$h = \frac{v^2}{2g} = 0.8 \, \text{m}$$(B错误)。横坐标每一小格时间为 $$0.1 \, \text{s}$$(C正确)。撞击地面时速度 $$5 \, \text{m/s}$$,反弹速度 $$4 \, \text{m/s}$$,动量变化 $$\Delta p = 0.5 \times (5 + 4) = 4.5 \, \text{kg} \cdot \text{m/s}$$,作用时间约 $$0.1 \, \text{s}$$,平均作用力 $$F = \frac{\Delta p}{\Delta t} = 45 \, \text{N}$$(D错误)。答案为 C。
4. 解析:
气体喷出的质量流量 $$\frac{dm}{dt} = \rho S v$$,动量变化率 $$\frac{dp}{dt} = \rho S v^2$$。由动量守恒,墙壁受到的冲量 $$I = \rho S v^2 \Delta t$$。答案为 C。
5. 解析:
单位时间内撞击建筑物的空气质量 $$m = \rho S v$$,动量变化 $$\Delta p = m v = \rho S v^2$$,风力 $$F = \frac{\Delta p}{\Delta t} = \rho S v^2$$。答案为 B。
6. 解析:
单位时间内附着在飞船上的微陨石质量 $$\frac{dm}{dt} = \rho S v = 1 \times 10^{-7} \times 2 \times 10^4 = 2 \times 10^{-3} \, \text{kg/s}$$。助推力增量 $$F = v \cdot \frac{dm}{dt} = 10^4 \times 2 \times 10^{-3} = 20 \, \text{N}$$。答案为 A。
7. 解析:
相对风速 $$v_{\text{相对}} = v_2 + v_1$$,单位时间内撞击车头的空气质量 $$m = \rho S (v_2 + v_1)$$,风力 $$F = \rho S (v_2 + v_1)^2$$。答案为 A。
8. 解析:
水流横截面积 $$A = \frac{\pi d^2}{4}$$,质量流量 $$\frac{dm}{dt} = \rho A v = \frac{\pi \rho d^2 v}{4}$$。冲力 $$F = v \cdot \frac{dm}{dt} = \frac{\pi \rho d^2 v^2}{4}$$。答案为 D。
9. 解析:
水流量 $$\frac{dm}{dt} = \rho \pi r^2 v$$,动量变化率 $$\frac{dp}{dt} = \rho \pi r^2 v^2$$,冲击力 $$F = \rho \pi r^2 v^2$$。答案为 C。
10. 解析:
雨滴竖直速度 $$v = 10 \, \text{m/s}$$,单位时间内水位上升 $$h = \frac{18 \times 10^{-3}}{1800} = 10^{-5} \, \text{m/s}$$。单位面积上的质量流量 $$\frac{dm}{dt} = \rho h = 10^3 \times 10^{-5} = 0.01 \, \text{kg/(m}^2 \cdot \text{s)}$$。压强 $$P = v \cdot \frac{dm}{dt} = 10 \times 0.01 = 0.1 \, \text{Pa}$$。答案为 A。
.jpg)