.jpg)
正确率40.0%质量为$${{m}}$$的铁锤从高$${{h}}$$处落下，打在水泥桩上，铁锤与水泥桩撞击的时间是$${{t}}$$，撞击时，铁锤对桩的平均冲击力大小为（）
A
A.$$\frac{m \sqrt{2 g h}} {t}+m g$$
B.$$\frac{m \sqrt{2 g h}} {t}-m g$$
C.$$\frac{m \sqrt{g h}} {t}+m g$$
D.$$\frac{m \sqrt{g h}} {t}-m g$$
2、['动量定理的定量计算'， '自由落体运动的规律'， '竖直上抛运动']正确率40.0%蹦床是运动员在一张绷紧的弹性网上蹦跳$${、}$$翻滚并做各种空中动作的项目.一个质量为$${{6}{0}{k}{g}}$$的运动员，从离水平网面$${{3}{.}{2}{m}}$$高处自由下落，着网后沿竖直方向蹦回到离水平网面$${{5}{.}{0}{m}}$$高处.已知运动员与网接触的时间为$${{1}{.}{2}{s}}$$，重力加速度$$g=1 0 m / s^{2}$$，则该段时间内网对运动员的平均作用力大小为（）
A
A.$$1 5 0 0 N$$
B.$$1 1 0 0 N$$
C.$$1 0 0 0 N$$
D.$${{9}{0}{0}{N}}$$
3、['动量定理的定量计算']正确率60.0%一个质量为$$0. 1 8 k g$$的垒球，以$$2 0 m / s$$的水平速度飞向球棒，被球棒击打后反向水平飞回。设击打过程球棒对垒球的平均作用力大小为$${{9}{0}{0}{N}}$$，作用时间为$$0. 0 1 s$$。则被球棒击打后垒球反向水平速度大小为（）
A
A.$$3 0 m / s$$
B.$$4 0 m / s$$
C.$$5 0 m / s$$
D.$$7 0 m / s$$
4、['动量定理的定量计算'， 'v-t图像综合应用'， '滑动摩擦力大小'， '牛顿运动定律分析滑块-滑板模型问题'， '牛顿第二定律的内容及理解']正确率40.0%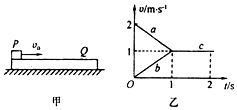
如图甲所示，长$${{2}{m}}$$
C
A.在$${{0}{−}{2}{s}}$$内，木板$${{Q}}$$下表面与水平面之间有摩擦力
B.在$${{0}{−}{2}{s}}$$内，摩擦力对$${{Q}}$$的冲量是$${{2}}$$$${{N}{⋅}{s}}$$
C.$${{P}{、}{Q}}$$之间的动摩擦因数为$${{0}{.}{1}}$$
D.$${{P}}$$相对$${{Q}}$$静止的位置在$${{Q}}$$木板的最右端
5、['动量定理的定量计算'， '动能定理的简单应用']正确率40.0%质量是$${{4}{0}{k}{g}}$$的铁锤从$${{5}{m}}$$高处落下，打在水泥桩上，与水泥桩撞击的时间是$$0. 0 5 s$$，铁锤被向上反弹的高度为$$0. 2 m， ~ g$$取$$1 0 m / s^{2}$$，则撞击时铁锤对桩的平均冲击力大小为（）
A
A.$$\ 1 0 0 0 0 N$$
B.$$9 6 0 0 N$$
C.$$8 4 0 0 N$$
D.$$8 0 0 0 N$$
6、['动量与能量的其他综合应用'， '动量定理的定量计算'， '动量守恒定律内容，应用范围和推导'， '用动量守恒定律分析滑块-木板模型']正确率19.999999999999996%质量为 $${{m}}$$$${{=}{1}{k}{g}}$$的小木块(可看成质点$${{)}}$$，放在质量为 $${{M}}$$$${{=}{5}{k}{g}}$$的长木板的左端，如图所示。长木板放在光滑水平桌面上。小木块与长木板间的动摩擦因数 $${{μ}}$$$${{=}{{0}{.}{1}}}$$，长木板的长度 $${{L}}$$$${{=}{{2}{.}{5}}{m}}$$。系统处于静止状态。现为使小木块从长木板右端脱离出来，给小木块一个水平向右瞬时冲量 $${{I}}$$，则冲量 $${{I}}$$至少是( $${{g}}$$取$$1 0 \， m / s^{2} ) ( \phantom{h g a m} )$$
C
A.$$\frac{1} {6} N \cdot s$$
B.$$\frac{1} {\sqrt{6}} N \cdot s$$
C.$$\sqrt{6} N \cdot s$$
D.$${{6}{N}{⋅}{s}}$$
7、['动量定理的定量计算'， '动能的定义及表达式'， '利用动量定理求解其他问题'， '动能定理的简单应用']正确率40.0%有两个物体$${{a}}$$和$${{b}}$$，其质量分别为$${{m}_{a}}$$和$${{m}_{b}}$$，且$${{m}_{a}{>}{{m}_{b}}}$$，它们的初动量相同，若$${{a}}$$和$${{b}}$$分别受不变的阻力$${{F}_{a}}$$和$${{F}_{a}}$$的作用，经过相同的位移后速度减为零，所用的时间分别是$${{t}_{a}}$$和$${{t}_{b}}$$，则（）
C
A.$${{F}_{a}{>}{{F}_{a}}}$$，且$${{t}_{a}{>}{{t}_{b}}}$$
B.$${{F}_{a}{>}{{F}_{a}}}$$，且$${{t}_{a}{<}{{t}_{b}}}$$
C.$${{F}_{a}{<}{{F}_{a}}}$$，且$${{t}_{a}{>}{{t}_{b}}}$$
D.$${{F}_{a}{<}{{F}_{a}}}$$，且$${{t}_{a}{<}{{t}_{b}}}$$
8、['动量定理的定量计算'， '动能定理的简单应用']正确率60.0%某物体在恒力$${{F}}$$作用下作直线运动，在$${{t}_{1}}$$时间内物体的速度由零增大到$${{v}{，}{F}}$$对物体做功$${{W}_{1}}$$，给物体冲量为$${{I}_{1}}$$；若在$${{t}_{2}}$$时间内物体的速度由$${{v}}$$增大到$${{2}{v}{，}{F}}$$对物体做功$${{W}_{2}}$$，给物体冲量为$${{I}_{2}}$$，下列结论正确的是（）
C
A.$$W_{1}=W_{2} \，， \， \， \， I_{1}=I_{2}$$
B.$$W_{1}=W_{2}， \， \， \， I_{1} > I_{2}$$
C.$$W_{1} < W_{2} \，， \， \， \， I_{1}=I_{2}$$
D.$$W_{1} > W_{2} \，， \， \， I_{1}=I_{2}$$
9、['动量定理的定量计算'， '用牛顿运动定律分析弹簧类问题'， '功能关系的应用']正确率40.0%如图所示，劲度系数为$${{k}}$$的轻弹簧的一端固定在墙上，另一端与置于水平面上质量为$${{m}}$$的物体$${{P}}$$接触，但未与物体$${{P}}$$连接，弹簧水平且无形变.现对物体$${{P}}$$施加一个水平向右的瞬时冲量，大小为$${{I}_{0}{，}}$$测得物体$${{P}}$$向右运动的最大距离为$${{x}_{0}{，}}$$之后物体$${{P}}$$被弹簧弹回最终停在初始位置左侧$${{2}{{x}_{0}}}$$处.已知弹簧始终在弹性限度内，物体$${{P}}$$与水平面间的动摩擦因数为$${{μ}{，}}$$重力加速度为$${{g}{，}}$$下列说法中正确的是（）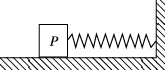
B
A.物体$${{P}}$$与弹簧作用的过程中，系统的最大弹性势为$$4 \mu m g x_{0}$$
B.最初对物体$${{P}}$$施加的瞬时冲量$$I_{0}=2 m \sqrt{2 \mu g x_{0}}$$
C.弹簧被压缩到最短之后的过程$${，{P}}$$先做加速度减小的加速运动，再做加速度减小的减速运动，最后做匀减速运动
D.物体$${{P}}$$整个运动过程，摩擦力的冲量与弹簧弹力的冲量大小相等、方向相反
10、['动量定理的定量计算'， 'v-t图像斜率意义，及v-t图像求加速度'， '匀变速直线运动平均速度和中间时刻速度公式'， 'v-t图像面积意义，及v-t图像求位移']正确率40.0%一辆汽车从静止开始从甲地出发，沿平直公路驶往乙地，其$${{v}{−}{t}}$$图象如图所示，在$${{O}{∼}{{t}_{0}}}$$和$$t_{0} \sim3 t_{0}$$两段时间内（）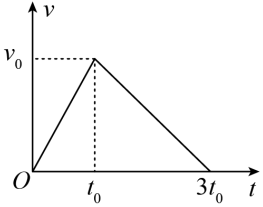
C
A.加速度大小之比为$${{1}{：}{2}}$$
B.位移大小之比为$${{2}{：}{3}}$$
C.平均速度大小之比为$${{1}{：}{1}}$$
D.合力的冲量大小之比为$${{2}{：}{1}}$$
1. 解析：
铁锤下落时的末速度由动能定理或自由落体公式可得：$$v = \sqrt{2gh}$$。撞击过程中，铁锤受到桩的平均冲击力$$F$$和重力$$mg$$，取向上为正方向，由动量定理：$$(F - mg)t = 0 - (-mv)$$，解得：$$F = \frac{m\sqrt{2gh}}{t} + mg$$。故选A。
2. 解析：
运动员下落时的速度：$$v_1 = \sqrt{2gh_1} = \sqrt{2 \times 10 \times 3.2} = 8 \, \text{m/s}$$（向下）。反弹时的速度：$$v_2 = \sqrt{2gh_2} = \sqrt{2 \times 10 \times 5} = 10 \, \text{m/s}$$（向上）。由动量定理，取向上为正方向：$$(F - mg)t = mv_2 - (-mv_1)$$，代入数据：$$(F - 600) \times 1.2 = 60 \times 10 + 60 \times 8$$，解得：$$F = 1500 \, \text{N}$$。故选A。
3. 解析：
设垒球反向速度为$$v$$，取反向为正方向，由动量定理：$$Ft = mv - (-mv_0)$$，代入数据：$$900 \times 0.01 = 0.18v + 0.18 \times 20$$，解得：$$v = 30 \, \text{m/s}$$。故选A。
4. 解析：
由图甲可知，$$0-2s$$内$$Q$$的加速度为$$1 \, \text{m/s}^2$$，说明$$Q$$受到$$P$$的滑动摩擦力，但$$Q$$下表面与水平面无相对运动，故无摩擦力，A错误。摩擦力对$$Q$$的冲量为$$f \cdot t = \mu mg \cdot t = 0.1 \times 1 \times 10 \times 2 = 2 \, \text{N} \cdot \text{s}$$，B正确。$$P$$的加速度为$$2 \, \text{m/s}^2$$，由牛顿第二定律：$$\mu mg = ma_P$$，解得$$\mu = 0.2$$，C错误。$$P$$相对$$Q$$滑动的位移为$$x = \frac{1}{2}a_P t^2 - \frac{1}{2}a_Q t^2 = 1 \, \text{m}$$，未达到$$Q$$的最右端，D错误。故选B。
5. 解析：
铁锤撞击前的速度：$$v_1 = \sqrt{2gh} = \sqrt{2 \times 10 \times 5} = 10 \, \text{m/s}$$（向下）。反弹速度：$$v_2 = \sqrt{2gh'} = \sqrt{2 \times 10 \times 0.2} = 2 \, \text{m/s}$$（向上）。由动量定理，取向上为正方向：$$(F - mg)t = mv_2 - (-mv_1)$$，代入数据：$$(F - 400) \times 0.05 = 40 \times 2 + 40 \times 10$$，解得：$$F = 8400 \, \text{N}$$。故选C。
6. 解析：
小木块脱离长木板的条件是两者达到共同速度时，小木块恰好滑到长木板右端。设冲量为$$I$$，小木块初速度$$v_0 = \frac{I}{m}$$。由动量守恒和能量关系：$$mv_0 = (m + M)v$$，$$\mu mgL = \frac{1}{2}mv_0^2 - \frac{1}{2}(m + M)v^2$$，联立解得：$$I = \sqrt{6} \, \text{N} \cdot \text{s}$$。故选C。
7. 解析：
初动量相同，$$m_a v_a = m_b v_b$$，且$$m_a > m_b$$，故$$v_a < v_b$$。由动能定理：$$F_a s = \frac{1}{2}m_a v_a^2$$，$$F_b s = \frac{1}{2}m_b v_b^2$$，因$$v_a < v_b$$，故$$F_a < F_b$$。由动量定理：$$t_a = \frac{m_a v_a}{F_a}$$，$$t_b = \frac{m_b v_b}{F_b}$$，代入$$v_a < v_b$$和$$F_a < F_b$$，可得$$t_a > t_b$$。故选C。
8. 解析：
由动能定理：$$W_1 = \frac{1}{2}mv^2$$，$$W_2 = \frac{1}{2}m(2v)^2 - \frac{1}{2}mv^2 = \frac{3}{2}mv^2$$，故$$W_1 < W_2$$。由动量定理：$$I_1 = mv$$，$$I_2 = 2mv - mv = mv$$，故$$I_1 = I_2$$。故选C。
9. 解析：
物体$$P$$向右运动的最大距离$$x_0$$时，弹性势能最大，由能量守恒：$$\frac{1}{2}kx_0^2 + \mu mg x_0 = \frac{1}{2}mv_0^2$$，其中$$v_0 = \frac{I_0}{m}$$。最终停在左侧$$2x_0$$处，说明总路程为$$4x_0$$，由动能定理：$$\mu mg \cdot 4x_0 = \frac{1}{2}mv_0^2$$，解得：$$I_0 = 2m\sqrt{2\mu g x_0}$$，B正确。最大弹性势能$$E_p = \frac{1}{2}kx_0^2$$，不等于$$4\mu mg x_0$$，A错误。弹簧压缩后，$$P$$先减速到零再反向加速，最后匀减速停止，C错误。摩擦力冲量与弹簧弹力冲量大小相等方向相反，D正确。故选BD。
10. 解析：
由$$v-t$$图斜率得加速度之比为$$1:2$$，A正确。位移之比为面积之比$$1:2$$，B错误。平均速度均为$$\frac{v_0}{2}$$，C正确。冲量$$I = F \cdot t$$，合力之比为$$1:2$$，时间之比为$$1:2$$，故冲量之比为$$1:4$$，D错误。故选AC。