.jpg)
正确率40.0%如图所示，在光滑的水平地面上停放着质量为$${{m}}$$的装有$$\frac{1} {4}$$弧形槽的小车$${{.}}$$现有一质量也为$${{m}}$$的小球以$${{v}_{0}}$$的水平速度沿切线水平的槽口向小车滑去，不计一切摩擦，则（）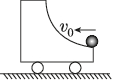
C
A.在相互作用的过程中，小车和小球组成的系统总动量守恒
B.小球从右侧离开车后，对地将向右做平抛运动
C.小球从右侧离开车后，对地将做自由落体运动
D.小球从右侧离开车后，小车的速度有可能大于$${{v}_{0}}$$
2、['平抛运动基本规律及推论的应用'， '动量守恒定律内容，应用范围和推导']正确率40.0%$${{A}{，}{B}}$$两球之间压缩一根轻弹簧(未拴连$${{)}}$$，静置于光滑水平桌面上。已知$${{A}{，}{B}}$$两球质量分别为$${{2}{m}}$$和$${{m}}$$.当用板挡住$${{A}}$$球而只释放$${{B}}$$球时，弹簧恢复原长后，$${{B}}$$球离开桌面落于距桌边距离为$${{x}}$$的水平地面上，如图所示。当在原位置用同样的程度压缩弹簧，取走$${{A}}$$球左边的挡板，将$${{A}{、}{B}}$$两球同时释放，弹簧恢复原长后，$${{B}}$$球离开桌面。$${{B}}$$球的落地点距离桌边距离为（）
C
A.$${\sqrt {3}{x}}$$
B.$${{x}}$$
C.$$\frac{\sqrt6} {3} x$$
D.$$\frac{x} {3}$$
3、['动量守恒定律内容，应用范围和推导'， '动量守恒-系统受到外力矢量和为0']正确率40.0%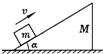
如图所示，质量为$${{M}}$$
D
A.物体在到达斜面的最高位置时
B.物体从斜面上开始下滑时
C.物体与斜面速度相等时
D.物体与斜面开始分离时
4、['动量守恒定律内容，应用范围和推导'， 'α衰变的特点、本质及其方程的写法'， 'β衰变的特点、本质及其方程的写法'， '反冲与爆炸']正确率60.0%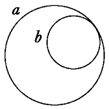
在垂直于纸面的匀强磁场中，有一原来静止的原子核，该核衰变后，放出的带电粒子和反冲核的运动轨迹分别如图中$${{a}{、}{b}}$$
B
A.该核发生的是$${{α}}$$衰变
B.该核发生的是$${{β}}$$衰变
C.$${{a}}$$表示反冲核的运动轨迹
D.磁场方向一定垂直纸面向里
5、['动量守恒定律内容，应用范围和推导'， '动量守恒-系统受到外力矢量和为0']正确率40.0%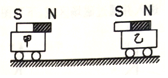
如图，将两条磁性很强且完全相同的磁铁分别固定在质量相等的小车上，若两磁铁的$${{N}{、}{S}}$$
C
A.先放开左手，再放开右手后，系统总动量向左
B.先放开左手，再放开右手后，系统动量不守恒
C.两手同时放开后，系统总动量始终为零
D.两手同时放开后，系统总动量不守恒
6、['动量守恒定律内容，应用范围和推导'， '动量守恒-系统受到外力矢量和为0'， '判断系统机械能是否守恒']正确率60.0%如图，小车甲与弹簧相连在光滑水平面上做往复运动，小车乙向右做匀速直线运动。取小车甲和弹簧作为研究系统，则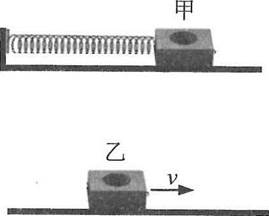
D
A.以地面为参考系，该系统动量与机械能守恒均守恒
B.以地面为参考系，该系统动量守恒但机械能不守恒
C.以小车乙为参考系，该系统动量不守恒但机械能守恒
D.以小车乙为参考系，该系统动量与机械熊均不守恒
7、['动量守恒定律内容，应用范围和推导'， 'α衰变的特点、本质及其方程的写法']正确率40.0%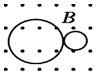
静止在匀强磁场中的某放射性原子核，沿垂直于磁场方向衰变放出一个$${{α}}$$
B
A.$${{8}{6}}$$
B.$${{9}{0}}$$
C.$${{8}{8}}$$
D.$${{9}{2}}$$
8、['动量守恒定律内容，应用范围和推导']正确率60.0%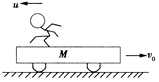
如图所示，质量为$${{M}}$$
C
A.$$\frac{M+m} {M} v_{0}$$
B.$$\frac{M+m} {M} v_{0}-\frac{m} {M} u$$
C.$$\frac{M+m} {M} v_{0}+\frac{m} {M} u$$
D.$${{v}_{0}{+}{u}}$$
9、['动量守恒定律内容，应用范围和推导']正确率60.0%一个静止的$${、}$$质量为$${{M}}$$的不稳定的原子核，当它放出质量为$${{m}}$$，速度为$${{v}}$$的粒子后，原子核剩余部分的速度为 （）
C
A.$${{−}{v}}$$
B.$$- \frac{M} {M-m} v$$
C.$$- \frac{m} {M-m} v$$
D.$$- \frac{m} {M} v$$
10、['动量守恒定律内容，应用范围和推导']正确率40.0%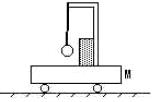
如图所示，质量为$${{m}}$$
C
A.向右匀速运动
B.向左匀速运动
C.静止不动
D.左右来回运动
1. 解析：
小车和小球组成的系统在水平方向不受外力，故水平方向动量守恒，但竖直方向有外力（支持力和重力），总动量不守恒，选项A错误。小球从右侧离开车时，水平方向动量守恒，设小车速度为$$v_1$$，小球速度为$$v_2$$，则有：
$$mv_0 = mv_1 + mv_2$$
由于弧形槽光滑，机械能守恒：
$$\frac{1}{2}mv_0^2 = \frac{1}{2}mv_1^2 + \frac{1}{2}mv_2^2$$
解得$$v_1 = v_0$$，$$v_2 = 0$$，即小球离开车时对地速度为0，做自由落体运动，选项C正确。小车速度不可能大于$$v_0$$，选项D错误。
答案：C
2. 解析：
第一次释放$$B$$球时，弹簧弹性势能转化为$$B$$球的动能：
$$E_p = \frac{1}{2}mv_B^2$$
$$B$$球平抛运动时间$$t$$相同，水平距离$$x = v_B t$$。
第二次同时释放$$A$$和$$B$$球，动量守恒：
$$0 = 2mv_A - mv_B'$$
机械能守恒：
$$E_p = \frac{1}{2} \cdot 2m v_A^2 + \frac{1}{2}mv_B'^2$$
解得$$v_B' = \frac{\sqrt{6}}{3}v_B$$，故落地点距离为$$\frac{\sqrt{6}}{3}x$$。
答案：C
3. 解析：
题目不完整，无法解析。
4. 解析：
由轨迹半径$$r = \frac{mv}{qB}$$可知，反冲核质量大、电荷多，轨迹半径小，故$$b$$为反冲核轨迹。若为$$α$$衰变，$$a$$应为$$α$$粒子（$$He^{2+}$$），但题目未明确电荷关系；若为$$β$$衰变，$$a$$为电子，$$b$$为反冲核。磁场方向无法确定。
答案：B、C
5. 解析：
两手同时放开时，系统合外力为零，动量守恒且总动量为零，选项C正确。若先后放开，系统受外力作用，动量不守恒，选项B正确。
答案：B、C
6. 解析：
以地面为参考系，弹簧弹力为内力，系统动量守恒，但机械能因弹簧做功不守恒（动能与弹性势能转化），选项B正确。以小车乙为参考系，系统受惯性力，动量不守恒，机械能守恒（仅弹性势能与动能转化），选项C正确。
答案：B、C
7. 解析：
设原子核质量为$$M$$，放出$$α$$粒子（质量$$4$$，电荷$$2$$）后，反冲核质量为$$M-4$$，电荷为$$Z-2$$。由动量守恒和半径公式：
$$\frac{r_α}{r_{\text{核}}} = \frac{q_{\text{核}}}{q_α} = \frac{Z-2}{2} = \frac{40}{10} = 4$$
解得$$Z=10$$，但选项无此答案，可能题目数据有误。
8. 解析：
设人跳离时车速度为$$v$$，水平动量守恒：
$$(M+m)v_0 = Mv + m(v-u)$$
解得$$v = \frac{M+m}{M}v_0 + \frac{m}{M}u$$。
答案：C
9. 解析：
由动量守恒：
$$0 = mv + (M-m)v'$$
解得剩余部分速度$$v' = -\frac{m}{M-m}v$$。
答案：C
10. 解析：
子弹射入沙袋过程动量守恒，沙袋获得速度后做圆周运动。子弹与沙袋系统动量不守恒（受绳子拉力），但机械能守恒（忽略摩擦）。最终沙袋可能静止或摆动，但题目条件不足。