.jpg)
正确率40.0%
如图所示，两辆质量相同的平板小车$${{a}{、}{b}}$$成一直线排列，静止在光滑水平地面上，原来静止在$${{a}}$$车上的一个小孩跳到$${{b}}$$，接着又立即从$${{b}}$$跳回$${{a}}$$车，他跳回$${{a}}$$车并相对$${{a}}$$车保持静止，此后（）
C
A.$${{a}{、}{b}}$$两车的速率相等
B.$${{a}}$$车的速率大于$${{b}}$$车的速率
C.$${{a}}$$车的速率小于$${{b}}$$车的速率
D.$${{a}{、}{b}}$$两车均静止
2、['动量守恒-系统受到外力矢量和为0']正确率40.0%如图所示，在粗糙水平面上，用水平轻绳连接的两个材料相同的物体$${{A}{、}{B}}$$，质量均为$${{m}}$$在水平恒力的作用下以速度$${{v}}$$做匀速运动，在$${{t}{=}{0}}$$时轻绳断开，在$${{F}}$$作用下继续前进，则下列说法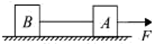
D
A.$${{t}{=}{0}}$$至$$t=\frac{2 m v} {F}$$时间内，$${{A}{、}{B}}$$的总动量守恒
B.$$t=\frac{2 m v} {F}$$时，$${{A}}$$的动量为$${{2}{m}{v}}$$
C.$$t=\frac{2 m v} {F}$$至$$t=\frac{3 m v} {F}$$时间内，$${{A}{、}{B}}$$的总动量不守恒
D.$$t=\frac{4 m v} {F}$$时，$${{A}}$$的动量为$${{2}{m}{v}}$$
3、['动量守恒-系统受到外力矢量和为0'， '人船模型']正确率60.0%一辆小车静止在光滑的水平面上，一个人从小车的一端走到另一端.对此，以下说法中错误的是（）
C
A.人匀速走动时，车也一定反向匀速运动
B.人停止走动时，车也停止运动
C.人速与车速之比，等于人的质量与车的质量之比
D.整个过程中，车相对于地面的位移是一定值，与人走动的快慢无关
4、['动量守恒-系统受到外力矢量和为0'， '惯性及惯性现象'， '人船模型']正确率40.0%质量为$${{m}}$$的人站在长为$${{L}{、}}$$质量为$${{M}}$$的船一端$$( \， m < M )$$，人与船原来静止．不计水的阻力．当人从船一端走到另一端过程中，则（）
D
A.人在船上行走，人对船的冲量比船对人的冲量小，所以人向前运动得快
B.当人突然停止时，船由于惯性仍要运动
C.当该人从船头走到船尾时，人相对于地发生的位移为$$\frac{m L} {M+m}$$
D.当该人从船头走到船尾时，船相对于地发生的位移为$$\frac{m L} {M+m}$$
5、['安培力的大小简单计算及应用'， '动量定理的定量计算'， '动量守恒-系统受到外力矢量和为0'， '闭合电路欧姆定律内容、表达式、及其能量分析'， '感应电流方向的判定（右手定则）'， '导体棒或线圈切割磁感线时引起的感应电动势及计算'， '牛顿第二定律的简单应用']正确率40.0%如图所示，两根相距为$${{d}}$$的足够长的光滑金属导轨固定在水平面上，导轨电阻不计。磁感应强度为$${{B}}$$的匀强磁场与导轨平面垂直，长度略大于$${{d}}$$的两导体棒$${{M}{、}{N}}$$平行地放在导轨上，导体棒的电阻均为$${{R}{、}}$$质量均为$${{m}}$$，开始两导体棒静止，现给导体棒$${{M}}$$一个平行导轨向右的瞬时冲量$${{I}}$$，整个过程中导体棒与导轨接触良好，下列说法正确的是（）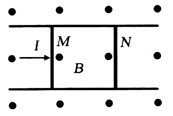
B
A.回路中始终存在逆时针方向的电流
B.棒$${{N}}$$的最大加速度为$$\frac{B^{2} I d^{2}} {2 m^{2} R}$$
C.回路中的最大电流为$$\frac{B I d} {m R}$$
D.棒$${{N}}$$获得的最大速度为$$\frac{I} {m}$$
6、['带电粒子在磁场中的运动'， '弹性碰撞'， '动量守恒-系统受到外力矢量和为0'， '受力分析'， '洛伦兹力的计算'， '安培力的方向判断（左手定则）'， '洛伦兹力的方向判断']正确率40.0%如图，空间中有$$B=2. 5 \times1 0^{4} T$$垂直纸面向里的匀强磁场。水平放置的管道内壁光滑，半径略小于管道内径$${、}$$带电量$$q=+1 \times1 0^{-4} C.$$质量$$m_{A}=1 k g$$的小球$${{A}}$$静止，与$${{A}}$$大小相等$${、}$$质量$$m_{B}=2 k g$$的不带电绝缘小球$${{B}}$$以速度$$v=3 m / s$$向右与$${{A}}$$发生弹性碰撞后，下列说法正确的是$$( g=1 0 m / s^{2} )$$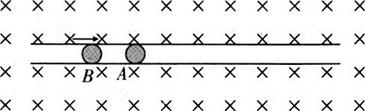
D
A.$${{B}}$$球碰后速度大小为$${{2}{m}{/}{s}}$$
B.$${{A}}$$球碰后对管道上表面有压力
C.$${{A}}$$球碰后对管道下表面有压力
D.$$A. ~ B. ~ C$$选项说法都不对
7、['动量守恒-系统受到外力矢量和为0'， '判断系统机械能是否守恒']正确率60.0%如图所示，在水平光滑地面上有$${{A}{、}{B}}$$两个木块，$${{A}{、}{B}}$$之间用一轻弹簧连接。$${{A}}$$靠在墙壁上，用力$${{F}}$$向左推$${{B}}$$使两木块之间弹簧压缩并处于静止状态。若突然撤去力$${{F}}$$，则下列说法中正确的是（）
C
A.木块$${{A}}$$离开墙壁前，$${{A}{、}{B}}$$和弹簧组成的系统动量守恒，机械能也守恒
B.木块$${{A}}$$离开墙壁前，$${{A}{、}{B}}$$和弹簧组成的系统动量守恒，机械能不守恒
C.木块$${{A}}$$离开墙壁后，$${{A}{、}{B}}$$和弹簧组成的系统动量守恒，机械能也守恒
D.木块$${{A}}$$离开墙壁后，$${{A}{、}{B}}$$和弹簧组成的系统动量不守恒，但机械能守恒
8、['动量守恒-系统受到外力矢量和为0']正确率40.0%
如图所示，质量为$${{M}}$$
C
A.第一种较大
B.第二种较大
C.二者一样大
D.不能确定
9、['碰撞'， '动量守恒-系统受到外力矢量和为0'， '判断系统机械能是否守恒'， '单摆的周期及应用'， '利用牛顿第三定律解决问题']正确率40.0%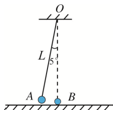
如图所示，一单摆摆长为$${{L}}$$
B
A.碰撞过程中，$${{A}}$$对$${{B}}$$的作用力大于$${{B}}$$对$${{A}}$$的作用力
B.碰撞过程中，$${{A}{、}{B}}$$系统的动量守恒
C.碰撞前后，$${{A}{、}{B}}$$系统的动能不变
D.碰撞后，$${{A}}$$的摆动周期变大
10、['动量守恒-系统受到外力矢量和为0']正确率40.0%质量为$${{M}}$$的小车静止在水平地面上，当质量为$${{m}}$$的人在小车上行走时，下列说法中正确的有（）
B
A.若地面光滑，人和车组成的系统总动量方向与小车运动方向相同
B.若地面光滑，人和车组成的系统动量守恒
C.无论地面是否光滑，人和车组成的系统动量都一定守恒
D.只有当人的质量远远小于车的质量时，人和车组成的系统动量才守恒
1. 解析：
小孩与两车组成的系统动量守恒。设小孩质量为 $$m$$，车质量为 $$M$$，小孩跳出 $$a$$ 车时的速度为 $$v$$，跳回 $$a$$ 车后的速度为 $$u$$。根据动量守恒：
第一次跳向 $$b$$ 车：$$mv = (M + m)u_b$$，解得 $$u_b = \frac{mv}{M + m}$$。
第二次跳回 $$a$$ 车：$$mv = (M + m)u_a$$，解得 $$u_a = \frac{mv}{M + m}$$。
由于 $$a$$ 车质量较大（$$M + m > M$$），其速率 $$u_a$$ 小于 $$b$$ 车的速率 $$u_b$$。故选 C。
2. 解析：
轻绳断开前，$$A$$ 和 $$B$$ 以速度 $$v$$ 匀速运动，总动量为 $$2mv$$。断开后，$$A$$ 受恒力 $$F$$ 作用，$$B$$ 不受外力，动量不守恒。
选项 A 错误，因为 $$t=0$$ 至 $$t=\frac{2mv}{F}$$ 时间内，$$A$$ 受外力 $$F$$，总动量不守恒。
选项 B 正确，$$A$$ 的动量增量为 $$F \cdot \frac{2mv}{F} = 2mv$$，总动量为 $$2mv$$。
选项 C 正确，$$A$$ 和 $$B$$ 的总动量在 $$t=\frac{2mv}{F}$$ 后不守恒。
选项 D 错误，$$t=\frac{4mv}{F}$$ 时，$$A$$ 的动量为 $$4mv$$。
题目要求选择不正确的选项，故选 D。
3. 解析：
人与小车组成的系统动量守恒。设人质量为 $$m$$，车质量为 $$M$$，人速度为 $$v$$，车速度为 $$V$$。由动量守恒：$$mv = MV$$，即 $$\frac{v}{V} = \frac{M}{m}$$。
选项 A 正确，人匀速走动时车反向匀速运动。
选项 B 正确，人停止时车也停止。
选项 C 错误，人速与车速之比应为车的质量与人的质量之比。
选项 D 正确，车相对于地面的位移与人走动快慢无关。
题目要求选择错误的选项，故选 C。
4. 解析：
人与船组成的系统动量守恒。设人相对于船的速度为 $$u$$，船相对于地面的速度为 $$V$$。由动量守恒：$$m(u - V) = MV$$，解得 $$V = \frac{mu}{M + m}$$。
人相对于地面的位移为 $$x = \frac{ML}{M + m}$$，船相对于地面的位移为 $$d = \frac{mL}{M + m}$$。
选项 A 错误，冲量大小相等。
选项 B 正确，船有惯性。
选项 C 错误，人相对于地面的位移为 $$\frac{ML}{M + m}$$。
选项 D 正确，船相对于地面的位移为 $$\frac{mL}{M + m}$$。
故选 D。
5. 解析：
导体棒 $$M$$ 获得初速度 $$v_0 = \frac{I}{m}$$。两棒在磁场中运动时，产生感应电动势 $$E = Bdv$$，回路电流 $$I = \frac{E}{2R} = \frac{Bdv}{2R}$$。
选项 A 错误，电流方向会变化。
选项 B 正确，$$N$$ 的最大加速度为 $$a = \frac{BId}{2mR}$$。
选项 C 正确，最大电流为 $$\frac{BId}{mR}$$。
选项 D 错误，$$N$$ 的最大速度为 $$\frac{I}{2m}$$。
故选 B 和 C，但题目可能为单选，需进一步确认。
6. 解析：
弹性碰撞后，$$B$$ 球速度为 $$v_B' = \frac{(m_B - m_A)v}{m_A + m_B} = 1 \, \text{m/s}$$，$$A$$ 球速度为 $$v_A' = \frac{2m_Bv}{m_A + m_B} = 2 \, \text{m/s}$$。
$$A$$ 球受洛伦兹力 $$F = qv_A'B = 5 \, \text{N}$$，重力 $$G = m_Ag = 10 \, \text{N}$$，合力向下，故对管道下表面有压力。
选项 A 错误，$$B$$ 球速度为 $$1 \, \text{m/s}$$。
选项 C 正确。
故选 C。
7. 解析：
$$A$$ 离开墙壁前，系统受墙壁外力，动量不守恒，但机械能守恒。$$A$$ 离开墙壁后，系统动量守恒且机械能守恒。
选项 C 正确。
故选 C。
8. 解析：
题目不完整，无法解析。
9. 解析：
碰撞过程中，$$A$$ 和 $$B$$ 的作用力大小相等，动量守恒。弹性碰撞动能不变。单摆周期 $$T = 2\pi\sqrt{\frac{L}{g}}$$ 与质量无关，故周期不变。
选项 B 和 C 正确，但题目可能为单选，需进一步确认。
10. 解析：
若地面光滑，人和车组成的系统动量守恒。若地面不光滑，系统动量不守恒。
选项 B 正确。
故选 B。