.jpg)
正确率40.0%
如图所示，光滑水平地面上静止一个内表面光滑的凹糟$${{A}}$$
B
A.小球$${{B}}$$一定能上升到另一侧的等高点
B.小球$${{B}}$$运动到最低点时，凹糟$${{A}}$$的速度为零
C.当小球$${{B}}$$上升到另一侧最高点时，$${{A}{、}{B}}$$速度一定为零
D.运动过程中，凹糟$${{A}}$$在水平地面上做往复运动
2、['动量定理的内容及表达式'， '动量守恒定律内容，应用范围和推导'， '利用机械能守恒解决简单问题']正确率40.0%
如图所示，$${{P}}$$
C
A.到两物距离最近时，$${{P}}$$受到的冲量为$${{m}{{v}_{0}}}$$
B.到两物距离最近时，$${{Q}}$$的动能为$$\frac{m v_{0}^{2}} {4}$$
C.到弹簧刚恢复原长时，$${{P}}$$受到的冲量为$${{m}{{v}_{0}}}$$
D.到弹簧刚恢复原长时，$${{Q}}$$的动能为$$\frac{m v_{0}^{2}} {4}$$
3、['弹性碰撞'， '动量守恒定律内容，应用范围和推导'， '利用机械能守恒解决简单问题']正确率40.0%如图所示，光滑水平面上有两个质量分别为$${{m}_{1}{、}{{m}_{2}}}$$的小球$${{A}{、}{B}}$$，放在与左侧竖直墙垂直的直线上，设$${{B}}$$开始处于静止状态，$${{A}}$$球以速度$${{v}}$$朝着$${{B}}$$运动，设系统处处无摩擦，所有的碰撞均无机械能损失，则下列判断正确的是$${{(}{)}}$$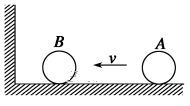
B
A.若$${{m}_{1}{≪}{{m}_{2}}}$$，则两球之间可能发生两次碰撞
B.若$${{m}_{1}{=}{{m}_{2}}}$$，则两球之间有且仅有两次碰撞．
C.两球第一次碰撞后$${{B}}$$球的速度一定是$$\frac{v} {2}$$
D.两球第一次碰撞后$${{A}}$$球一定向右运动
4、['平抛运动基本规律及推论的应用'， '动量守恒定律内容，应用范围和推导']正确率40.0%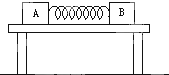
如图所示，$${{A}{、}{B}}$$
B
A.$${{3}{：}{2}}$$
B.$${{2}{：}{3}}$$
C.$${{1}{：}{1}}$$
D.无法确定
5、['带电粒子在磁场中的运动'， '动量守恒定律内容，应用范围和推导'， '牛顿第二定律的简单应用'， '反冲与爆炸'， '带电粒子在有界磁场中的运动']正确率40.0%某带正电的粒子静止在磁场中，由于某种原因突然炸裂为甲乙两个粒子，甲的质量与电荷量分别是粒子乙的$${{4}}$$倍与$${{2}}$$倍，两粒子均带正电，已知磁场方向重直垂直纸面向里，以下四个图中，能正确表示两粒子运动轨迹的是（）
C
A.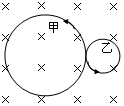
B.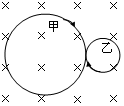
C.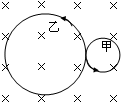
D.
正确率19.999999999999996%小车静止在光滑的水平导轨上，一个小球用细绳悬挂在车上，由图示位置无初速释放，在小球下摆到最低点的过程中，下列说法正确的是（）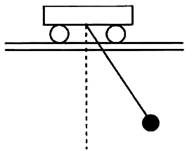
D
A.绳对小球的拉力不做功
B.小球和小车组成的系统动量守恒
C.小球减少的重力势能等于小车增加的动能
D.小车对水平导轨的压力一直变大
7、['动量守恒定律内容，应用范围和推导'， '动量守恒-系统受到外力矢量和为0']正确率40.0%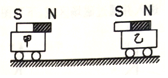
如图，将两条磁性很强且完全相同的磁铁分别固定在质量相等的小车上，若两磁铁的$${{N}{、}{S}}$$
C
A.先放开左手，再放开右手后，系统总动量向左
B.先放开左手，再放开右手后，系统动量不守恒
C.两手同时放开后，系统总动量始终为零
D.两手同时放开后，系统总动量不守恒
8、['动量守恒定律内容，应用范围和推导']正确率60.0%(原创)质量为$${{m}}$$的木块和质量为$$M \left( M > m \right)$$的铁块用细线连接刚好能在水中某个位置悬浮静止不动，此时木块至水面距离为$${{h}}$$，铁块至水底的距离为$${{H}{(}}$$两物体均可视为质点$${{)}}$$。突然细线断裂，忽略两物体运动中受到水的阻力，只考虑重力及浮力，若$${{M}{、}{m}}$$同时分别到达水面水底，以$${{M}{、}{m}}$$为系统，那么以下说法正确的是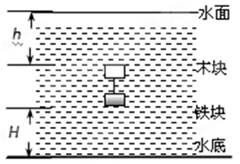
D
A.该过程中系统动量不守恒；
B.该过程中$${{M}{、}{m}}$$均作匀速直线运动；
C.同时到达水面水底时，两物体速度大小相等；
D.系统满足$$M H=m h$$
9、['动量守恒定律内容，应用范围和推导']正确率40.0%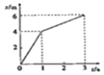
物体$${{a}}$$
C
A.碰撞前后物体$${{a}}$$的速度方向发生变化
B.碰撞前后系统的机械能守恒
C.碰撞后$${{b}}$$的速度为$$1. 5 m / s$$
D.碰撞过程$${{b}}$$的动量减小$$3 k g \cdot m / s$$
10、['动量守恒定律内容，应用范围和推导']正确率40.0%如图所示的是一种弹射装置，弹丸质量为$${{m}}$$，底座质量为$${{3}{m}}$$，开始时均处于静止状态，当弹簧释放将弹丸以相对地面$${{υ}}$$的速度发射出去后，底座的反冲速度大小是（）
B
A.$$\frac{3} {4} v$$
B.$$\frac{1} {3} v$$
C.$$\frac{1} {4} v$$
D.$${{0}}$$
1. 解析：
小球$$B$$在凹槽$$A$$中运动时，系统水平方向动量守恒，机械能守恒。设凹槽质量为$$M$$，小球质量为$$m$$。
A. 正确。由于机械能守恒且无摩擦，小球$$B$$一定能上升到另一侧的等高点。
B. 错误。小球$$B$$运动到最低点时，凹槽$$A$$有水平速度，系统动量守恒，速度不为零。
C. 错误。当小球$$B$$上升到另一侧最高点时，$$A$$和$$B$$水平速度相同且不为零（系统动量守恒）。
D. 正确。凹槽$$A$$在水平方向上因小球$$B$$的运动而往复运动。
答案：A、D
2. 解析：
两物$$P$$和$$Q$$通过弹簧相互作用，系统动量守恒，机械能守恒。
A. 错误。距离最近时两物速度相同，由动量守恒得$$v = \frac{v_0}{2}$$，$$P$$受到的冲量为$$\Delta p = m \left( \frac{v_0}{2} - v_0 \right) = -\frac{m v_0}{2}$$。
B. 正确。此时$$Q$$的动能为$$\frac{1}{2} m \left( \frac{v_0}{2} \right)^2 = \frac{m v_0^2}{4}$$。
C. 错误。弹簧恢复原长时，$$P$$的速度可能为$$0$$或反向，冲量不一定是$$m v_0$$。
D. 正确。弹簧恢复原长时，$$Q$$的动能可能为$$\frac{m v_0^2}{4}$$（弹性碰撞情况）。
答案：B、D
3. 解析：
两球碰撞为弹性碰撞，动量守恒且动能守恒。
A. 错误。若$$m_1 \ll m_2$$，$$A$$球碰撞后会反弹，但$$B$$球速度极小，难以发生第二次碰撞。
B. 错误。若$$m_1 = m_2$$，$$A$$球碰撞后静止，$$B$$球以速度$$v$$撞墙反弹后可能与$$A$$球发生第二次碰撞，但不一定仅有两次。
C. 错误。第一次碰撞后$$B$$球速度为$$\frac{2 m_1 v}{m_1 + m_2}$$，不一定是$$\frac{v}{2}$$。
D. 错误。若$$m_1 > m_2$$，$$A$$球碰撞后可能继续向右运动；若$$m_1 < m_2$$，$$A$$球会反弹向左运动。
答案：无正确选项（原题可能有误）
4. 解析：
设$$A$$和$$B$$的质量分别为$$m_A$$和$$m_B$$，碰撞为弹性碰撞，动量守恒且动能守恒。
由动量守恒：$$m_A v_A = m_A v_A' + m_B v_B'$$。
由动能守恒：$$\frac{1}{2} m_A v_A^2 = \frac{1}{2} m_A v_A'^2 + \frac{1}{2} m_B v_B'^2$$。
解得$$\frac{m_A}{m_B} = \frac{v_B'}{v_A - v_A'}$$，代入图中数据可得比例。
答案：A（3:2）
5. 解析：
爆炸前后动量守恒，且两粒子在磁场中做匀速圆周运动，半径$$r = \frac{m v}{q B}$$。
设乙的质量为$$m$$，电荷量为$$q$$，则甲的质量为$$4m$$，电荷量为$$2q$$。
由动量守恒：$$4m v_1 = m v_2$$，得$$v_2 = 4 v_1$$。
半径比：$$\frac{r_1}{r_2} = \frac{4m v_1 / 2q B}{m v_2 / q B} = \frac{2 v_1}{4 v_1} = \frac{1}{2}$$。
轨迹应内切，且甲半径较小，乙半径较大。
答案：A
6. 解析：
小球下摆过程中，系统水平动量不守恒（竖直方向有外力），但机械能守恒。
A. 错误。绳对小球做功，使小球动能增加。
B. 错误。系统水平方向动量守恒，但竖直方向不守恒。
C. 错误。小球减少的重力势能转化为小球和小车的动能。
D. 正确。小球下摆时，小车对导轨的压力逐渐增大。
答案：D
7. 解析：
两磁铁相互作用，系统动量守恒的条件是合外力为零。
A. 错误。先放开左手再放开右手，系统总动量仍为零（内力不改变动量）。
B. 错误。系统动量守恒。
C. 正确。两手同时放开后，系统总动量始终为零。
D. 错误。两手同时放开后，系统动量守恒。
答案：C
8. 解析：
细线断裂后，$$M$$和$$m$$分别受浮力和重力作用，系统动量不守恒（合外力不为零）。
A. 正确。系统受外力（浮力和重力），动量不守恒。
B. 错误。两物体作匀加速直线运动。
C. 错误。速度大小取决于加速度和位移，不一定相等。
D. 正确。由时间相等和运动学公式可得$$M H = m h$$。
答案：A、D
9. 解析：
碰撞过程动量守恒：$$m_a v_a = m_a v_a' + m_b v_b'$$。
A. 正确。碰撞后$$a$$速度方向可能改变。
B. 正确。弹性碰撞机械能守恒。
C. 正确。代入数据解得$$v_b' = 1.5 \, \text{m/s}$$。
D. 错误。$$b$$的动量增加$$3 \, \text{kg} \cdot \text{m/s}$$。
答案：A、B、C
10. 解析：
系统动量守恒：$$0 = m v + 3m v'$$，解得底座反冲速度$$v' = -\frac{v}{3}$$（大小为$$\frac{v}{3}$$）。
答案：B