.jpg)
正确率40.0%质量为$${{m}}$$、速度为$${{v}}$$的$${{A}}$$球跟质量为$${{4}{m}}$$的静止$${{B}}$$球发生正碰。碰撞可能是弹性的，也可能是非弹性的，因此，碰撞后$${{B}}$$球的速度可能是不同的值。则碰撞后$${{B}}$$球的速度可能为$${{(}{)}}$$
A.$$0. 1 5 v$$
B.$${{0}{.}{3}{v}}$$
C.$$0. 4 5 v$$
D.$${{0}{.}{5}{v}}$$
2、['匀变速直线运动的位移与时间的关系'， '动量定理内容及应用'， '对动量守恒条件的理解']正确率80.0%某战士静止站在冰面上来检验一款新型喷火枪的性能，在战士举枪水平射击的一小段时间$${{Δ}{t}}$$内，喷火枪连续均匀喷火消耗的油料体积为$${{Q}}$$，已知战士和喷火枪的总质量为$${{m}}$$，油料喷出时相对地的速度恒为$${{v}}$$，油料的密度为$${{ρ}}$$，不计人与冰面间的摩擦及喷火过程中人和枪的总质量的改变，则战士在$${{Δ}{t}}$$时间内后退的距离为$${{(}{)}}$$
A.$$\frac{\rho Q v \Delta t^{2}} {m}$$
B.$$\frac{2 \rho Q v \Delta t} {m}$$
C.$$\frac{\rho Q v \Delta t^{2}} {2 m}$$
D.$$\frac{\rho Q v \Delta t} {2 m}$$
3、['碰撞'， '对动量守恒条件的理解']正确率40.0%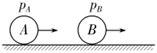
在光滑水平面上，有$${{A}}$$、$${{B}}$$两个小球向右沿同一直线运动，取向右为正，两球的动量分别是$$p_{A}=5 k g \cdot m / s$$，$$p_{B}=7 k g \cdot m / s$$，如图所示，若能发生正碰，则碰后两球的动量增量$${{Δ}{{p}_{A}}}$$、$${{Δ}{{p}_{B}}}$$可能是$${{(}{)}}$$
A.$$\Delta p_{A}=-3 k g \cdot m / s$$，$$\Delta p_{B}=3 k g \cdot m / s$$
B.$$\Delta p_{A}=3 k g \cdot m / s$$，$$\Delta p_{B}=3 k g \cdot m / s$$
C.$$\Delta p_{A}=-1 0 k g \cdot m / s$$，$$\Delta p_{B}=1 0 k g \cdot m / s$$
D.$$\Delta p_{A}=3 k g \cdot m / s$$，$$\Delta p_{B}=-3 k g \cdot m / s$$
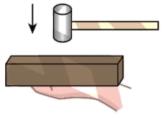
4、['利用动量定理解释有关物理现象'， '动量定理内容及应用'， '冲量'， '对动量守恒条件的理解']正确率40.0%用质量为$${{m}}$$的小铁锤以速度$${{v}_{1}}$$向下击打一块质量为$${{M}}$$的砖块$${{(}}$$击打时间极短$${{)}}$$，击打后，小铁锤以$${\frac{1} {2}} v_{1}$$的速率反向弹回，已知砖块受到击打后在手中的缓冲时间为$${{t}}$$，重力加速度为$${{g}}$$，下列说法正确的是$${{(}{)}}$$
A.在击打过程中，铁锤所受合外力的冲量大小为$${\frac{1} {2}} m v_{1}$$
B.在击打过程中，铁锤重力的冲量大小为$${{m}{g}{t}}$$
C.砖头缓冲过程中，对手的压力大小为$${{M}{g}}$$
D.砖头缓冲过程中，对手的压力大小为$$M g+\frac{3 m v_{1}} {2 t}$$
5、['对动量守恒条件的理解'， '人船模型']正确率80.0%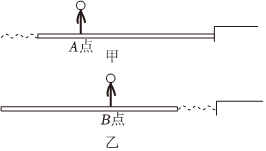
“独竹漂”是一项独特的黔北民间绝技。独竹漂高手们脚踩一根楠竹，漂行水上如履平地。如图甲所示，在平静的湖面上，一位女子脚踩竹竿抵达岸边，此时女子静立于竹竿$${{A}}$$点，一位摄影爱好者使用连拍模式拍下了该女子在竹竿上行走过程的系列照片，并从中选取了两张进行对比，其简化图如下。经过测量发现，甲、乙两张照片中$${{A}}$$、$${{B}}$$两点的水平间距约为$${{1}{c}{m}}$$，乙图中竹竿右端距离河岸约为$$1. 8 c m$$。照片的比例尺为$${{1}}$$：$${{4}{0}}$$。已知竹竿的质量约为$${{2}{5}{k}{g}}$$，若不计水的阻力，则该女子的质量约为$${{(}{)}}$$
A.$$4 1. 5 k g$$
B.$${{4}{5}{k}{g}}$$
C.$$4 7. 5 k g$$
D.$${{5}{0}{k}{g}}$$
6、['对动量守恒条件的理解'， '摩擦力做功'， '应用动能定理解决物体在传送带运动问题'， '用牛顿运动定律分析传送带模型']正确率40.0%如图所示，完全相同的$${{A}}$$、$${{B}}$$两物块随足够长的水平传送带按图中所示方向匀速运动，物块与传送带间摩擦因数均为$${{μ}}$$，重力加速度为$${{g}}$$。$${{A}}$$、$${{B}}$$间夹有少量炸药。炸药爆炸过程时间极短、内力极大。对$${{A}}$$、$${{B}}$$在炸药爆炸过程及随后的运动过程有下列说法，其中不正确的是$${{(}{)}}$$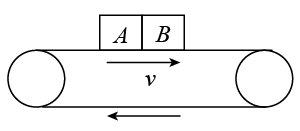
C
A.$${{A}}$$、$${{B}}$$系统在炸药爆炸后至$${{A}}$$、$${{B}}$$相对传送带静止的过程中动量守恒
B.炸药爆炸后至$${{A}}$$、$${{B}}$$相对传送带静止的过程摩擦力对$${{B}}$$做的功数值大小一定大于摩擦力对$${{A}}$$做的功的数值大小
C.若爆炸后$${{A}}$$、$${{B}}$$速度方向相反，则在炸药爆炸后至$${{A}}$$、$${{B}}$$相对传送带静止的过程$${{A}}$$与传送带之间产生的摩擦生热大于$${{B}}$$与传送带之间的摩擦生热
D.若$${{A}}$$、$${{B}}$$相对静止时两物块距离为$${{L}}$$，则$${{A}}$$、$${{B}}$$在炸药爆炸后至$${{A}}$$、$${{B}}$$相对传送带静止的过程用时
正确率40.0%
如图所示，木块$${{A}}$$、$${{B}}$$置于光滑水平桌面上，木块$${{A}}$$沿水平方向向左运动与$${{B}}$$相碰，碰后粘连在一起，将弹簧压缩到最短。则木块$${{A}}$$、$${{B}}$$和弹簧组成的系统，从$${{A}}$$、$${{B}}$$相碰到弹簧压缩至最短的整个过程中$${{(}{)}}$$
B
A.动量不守恒、机械能守恒
B.动量不守恒、机械能不守恒
C.动量守恒、机械能守恒
D.动量守恒、机械能不守恒
8、['动量与能量的其他综合应用'， '弹性碰撞'， '对动量守恒条件的理解']正确率80.0%如图所示，$${{A}}$$，$${{B}}$$，$${{C}}$$，$${{D}}$$，$${{E}}$$五个小球放在光滑水平面上，其中$$m_{A}=m_{E} < m_{B}=m_{C}=m_{D}$$，现让小球$${{A}}$$以初速度$${{v}_{0}}$$向右运动，已知小球之间的碰撞均为弹性碰撞，当所有的碰撞结束之后，下列说法正确的是$${{(}{)}}$$
B
A.$${{B}}$$，$${{C}}$$，$${{D}}$$三个小球静止，$${{A}}$$，$${{E}}$$两个小球运动
B.$${{B}}$$，$${{C}}$$两个小球静止，$${{A}}$$，$${{D}}$$，$${{E}}$$三个小球运动
C.$${{A}}$$，$${{B}}$$，$${{C}}$$，$${{D}}$$四个小球静止，小球$${{E}}$$运动
D.所有的小球都运动
9、['机械能守恒定律'， '对动量守恒条件的理解']正确率40.0%一名连同装备总质量为$${{M}}$$的航天员，脱离宇宙飞船后，在离飞船$${{x}}$$处与飞船处于相对静止状态。装备中有一个高压气源能以速度$${{v}{(}}$$以飞船为参考系$${{)}}$$喷出气体从而使航天员运动。如果航天员一次性向后喷出质量为$${{Δ}{m}}$$的气体，且在规定时间$${{t}}$$内返回飞船。下列说法正确的是$${{(}{)}}$$
A.喷出气体的质量$${{Δ}{m}}$$小于$$\frac{M x} {v t}$$
B.若高压气源喷出气体的质量不变但速度变大，则返回时间大于$${{t}}$$
C.若高压气源喷出气体的速度变大但动量不变，则返回时间小于$${{t}}$$
D.在喷气过程中，航天员、装备及气体所构成的系统动量和机械能均守恒
10、['光子动量及其公式'， '核裂变与核聚变'， '对动量守恒条件的理解'， '核反应']正确率40.0%$$^5_{3} L i ($$锂核$${{)}}$$是不稳定的，一个静止的$${^{5}_{3}{L}{i}}$$分裂时的核反应方程为$$\frac{5} {3} L i \to_{2}^{4} H e+X+\gamma$$，其中$${{X}}$$的动量大小为$${{p}_{1}}$$，$${^{4}_{2}{H}{e}}$$的动量大小为$${{p}_{2}}$$，$${{γ}}$$光子与$${^{4}_{2}{H}{e}}$$运动方向相同，普朗克常量为$${{h}{.}}$$则$${{(}{)}}$$
C
A.$${{X}}$$是中子
B.$${{X}}$$是电子
C.$${{γ}}$$光子的波长为$$\frac{h} {p_{1}-p_{2}}$$
D.$${{γ}}$$光子的波长为$$\frac{h} {p_{1}+p_{2}}$$
1. 解析：
根据动量守恒和能量守恒分析碰撞后$$B$$球的速度范围。
动量守恒：$$mv = mv_A + 4mv_B$$
弹性碰撞时动能守恒：$$\frac{1}{2}mv^2 = \frac{1}{2}mv_A^2 + \frac{1}{2} \cdot 4mv_B^2$$
解得$$v_B = \frac{2v}{5} = 0.4v$$（弹性碰撞）
完全非弹性碰撞时$$A$$、$$B$$共速：$$v_B = \frac{v}{5} = 0.2v$$
因此$$v_B$$的范围是$$0.2v \leq v_B \leq 0.4v$$，选项中只有$$B$$选项$$0.3v$$在此范围内。
答案：B
2. 解析：
喷火枪喷出油料的动量变化等于战士获得的动量。
喷出油料质量：$$m_{油} = \rho Q$$
喷出油料总动量：$$p_{油} = \rho Q v$$
战士获得的反冲动量：$$p_{人} = m u = \rho Q v$$，解得$$u = \frac{\rho Q v}{m}$$
后退距离：$$x = u \cdot \Delta t = \frac{\rho Q v \Delta t}{m}$$，但题目中油料是均匀喷出，实际后退距离应为$$x = \frac{1}{2} u \Delta t = \frac{\rho Q v \Delta t^2}{2m}$$。
答案：C
3. 解析：
碰撞需满足动量守恒和能量不增加条件。
总动量守恒：$$\Delta p_A + \Delta p_B = 0$$，排除$$B$$、$$D$$。
碰撞后动能不增加：$$\frac{(5 + \Delta p_A)^2}{2m_A} + \frac{(7 + \Delta p_B)^2}{2m_B} \leq \frac{5^2}{2m_A} + \frac{7^2}{2m_B}$$
代入$$A$$选项（$$\Delta p_A = -3$$，$$\Delta p_B = 3$$）满足条件。
答案：A
4. 解析：
铁锤击打过程动量变化：$$\Delta p = m\left(\frac{v_1}{2} - (-v_1)\right) = \frac{3}{2}mv_1$$，故$$A$$错误。
击打时间极短，重力冲量可忽略，$$B$$错误。
砖块缓冲过程受力分析：$$N = Mg + \frac{\Delta p}{t} = Mg + \frac{3mv_1}{2t}$$，$$D$$正确。
答案：D
5. 解析：
根据照片比例尺，$$A$$、$$B$$实际水平距离$$0.4m$$，竹竿右端距岸$$0.72m$$。
女子行走时系统动量守恒：$$m_{女} \cdot 0.4 = m_{竹} \cdot 0.72$$
解得女子质量：$$m_{女} = \frac{25 \times 0.72}{0.4} = 45kg$$。
答案：B
6. 解析：
$$A$$错误：爆炸后摩擦力为外力，系统动量不守恒。
$$B$$正确：若$$B$$速度更大，摩擦力做功更多。
$$C$$正确：$$A$$若反向运动，相对传送带位移更大，摩擦生热更多。
$$D$$错误：两物块减速时间应为$$t = \frac{L}{2\mu g}$$。
答案：A
7. 解析：
碰撞粘连过程机械能有损失，弹簧压缩过程机械能守恒，但全过程机械能不守恒。
碰撞过程外力为零，动量守恒；弹簧压缩过程墙对系统有外力，动量不守恒。
答案：B
8. 解析：
弹性碰撞中质量相等的小球会交换速度，质量不等时速度会传递。
最终$$B$$、$$C$$静止（质量相等交换速度后停止），$$A$$、$$D$$、$$E$$运动。
答案：B
9. 解析：
喷气动量：$$\Delta m \cdot v = M \cdot u$$，返回时间$$t = \frac{x}{u} = \frac{Mx}{\Delta m v}$$，故$$\Delta m = \frac{Mx}{vt}$$，$$A$$错误。
若$$v$$增大但$$\Delta m$$不变，则$$u$$增大，返回时间$$t$$减小，$$B$$错误。
若$$\Delta m v$$不变（动量不变），则$$t$$不变，$$C$$错误。
系统动量守恒但机械能不守恒（化学能转化为动能），$$D$$错误。
答案：无正确选项（原题可能有误）
10. 解析：
核反应方程质量数守恒：$$5 = 4 + A_X$$，得$$A_X = 1$$；电荷数守恒：$$3 = 2 + Z_X$$，得$$Z_X = 1$$，故$$X$$为质子，$$A$$、$$B$$均错误。
光子动量$$p_\gamma = p_1 - p_2$$（与$$He$$同向），波长$$\lambda = \frac{h}{p_\gamma} = \frac{h}{p_1 - p_2}$$，$$C$$正确。
答案：C