.jpg)
正确率80.0%根据量子理论：光子既有能量也有动量；光子的能量$${{E}}$$和动量$${{p}}$$之间的关系是$${{E}{=}{p}{c}}$$，其中$${{c}}$$为光速．由于光子有动量，照到物体表面的光子被物体吸收或被反射时都会对物体产生一定的冲量，也就对物体产生了一定的压强，这就是“光压”．根据动量定理可近似认为：当动量为$${{p}}$$的光子垂直照到物体表面，若被物体反射，则物体受到的冲量大小为$${{2}{p}}$$；若被物体吸收，则物体受到的冲量大小为$${{p}{.}}$$
有人设想在宇宙探测中用光作为动力推动探测器加速，探测器上安装有面积极大、反光率为$${{η}}$$的薄膜，并让它正对太阳．已知太阳光照射薄膜时对每平方米面积上的辐射功率为$${{P}_{0}}$$，探测器和薄膜的总质量为$${{m}}$$，薄膜面积为$${{S}}$$，则探测器的加速度大小．$${{(}}$$不考虑万有引力等其他的力$${{)}{(}{)}}$$
A.$$\frac{( 1+\eta) S \sqrt{P_{0}}} {c m}$$
B.$$\frac{( 1+\eta) P_{0} S} {c m}$$
C.$$\frac{( 2-\eta) P_{0} S} {c m}$$
D.$$\frac{( 2+\eta) P_{0}^{2} S} {c m}$$
2、['碰撞'， '对动量守恒条件的理解']正确率40.0%甲、乙两铁球质量分别是$$m_{1}=1 k g$$、$$m_{2}=2 k g$$，在光滑平面上沿同一直线运动，速度分别是$$v_{1}=6 m / s$$、$$v_{2}=2 m / s$$。甲追上乙发生正碰后两物体的速度有可能是$${{(}{)}}$$
A.$$v_{1}^{\prime}=7 m / s$$，$$v_{2}^{\prime}=1. 5 m / s$$
B.$$v_{1}^{\prime}=2 m / s$$，$$v_{2}^{\prime}=4 m / s$$
C.$$v_{1}^{\prime}=3. 5 m / s$$，$$v_{2}^{\prime}=3. 5 m / s$$
D.$$v_{1}^{\prime}=8 m / s$$，$$v_{2}^{\prime}=1 m / s$$
3、['判断系统机械能是否守恒'， '对动量守恒条件的理解'， '弹簧类机械能转化问题']正确率19.999999999999996%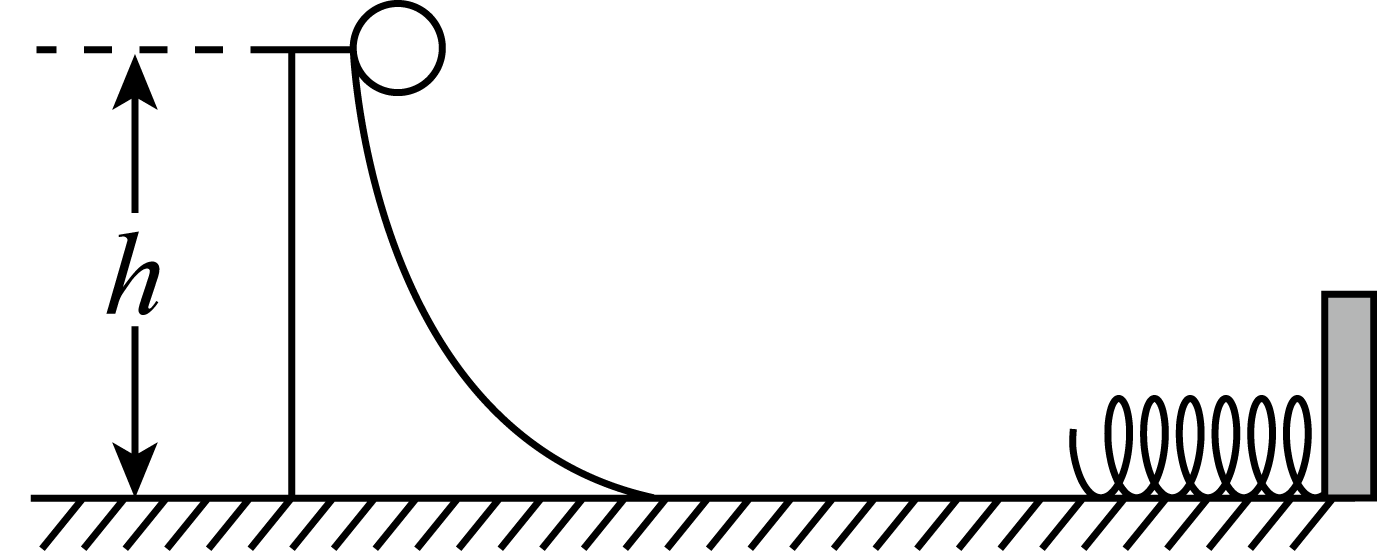
如图所示，弹簧的一端固定在竖直墙上，质量为$${{M}}$$的光滑弧形槽静止在光滑水平面上，底部与水平面平滑连接，一个质量为$$m ( m < M )$$的小球从槽高$${{h}}$$处开始自由下滑，下列说法正确的是$${{(}{)}}$$
D
A.在以后的运动过程中，小球和槽的水平方向动量始终守恒
B.在下滑过程中小球和槽之间的相互作用力始终不做功
C.全过程小球和槽、弹簧所组成的系统机械能守恒，且水平方向动量守恒
D.被弹簧反弹后，小球和槽的机械能守恒，但小球不能回到槽高$${{h}}$$处
4、['判断系统机械能是否守恒'， '对动量守恒条件的理解']正确率40.0%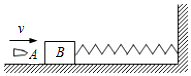
如图所示的装置中，木块$${{B}}$$与水平桌面间的接触是光滑的，子弹$${{A}}$$沿水平方向射入木块后留在木块内，将弹簧压缩到最短。把子弹、木块和弹簧合在一起作为研究对象，则此系统在子弹开始射入木块到弹簧压缩至最短的整个过程中$${{(}{)}}$$
D
A.动量守恒、机械能守恒
B.动量不守恒、机械能守恒
C.动量守恒、机械能不守恒
D.动量不守恒、机械能不守恒
5、['动量守恒-系统在某一方向不受力'， '判断系统机械能是否守恒'， '对动量守恒条件的理解'， '人船模型']正确率40.0%
如图将一质量为 $${{m}}$$ 的小球，从放置在光滑水平地面上质量为 $${{M}}$$ 的光滑半圆形槽的槽口 $${{A}}$$ 点由静止释放经过最低点 $${{B}}$$ 运动到 $${{C}}$$ 点，下列说法中正确的是 $${{(}{)}}$$
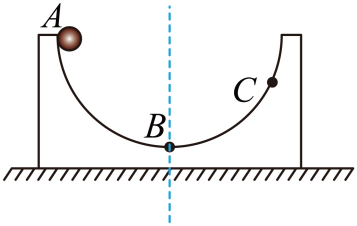
A.小球运动到圆形槽右侧最高点一定与$${{A}}$$点等高。
B.从$${{B}}$$运动到$${{C}}$$，半圆形槽和小球组成的系统动量守恒
C.从$${{A}}$$到$${{B}}$$再到$${{C}}$$，$${{C}}$$点可能是小球运动的最高点
D.从$${{A}}$$到$${{B}}$$，半圆形槽运动的位移一定大于小球在水平方向上运动的位移
6、['动量定理内容及应用'， '对动量守恒条件的理解']正确率0.0%如图$${{(}{a}{)}}$$，质量分别为$${{m}_{A}}$$、$${{m}_{B}}$$的$${{A}}$$、$${{B}}$$两物体用轻弹簧连接构成一个系统，外力$${{F}}$$作用在$${{A}}$$上，系统静止在光滑水平面上$${{(}{B}}$$靠墙面$${{)}}$$，此时弹簧形变量为$${{x}}$$，撤去外力并开始计时，$${{A}}$$、$${{B}}$$两物体运动的$${{a}{−}{t}}$$图像如图$${{(}{b}{)}}$$所示，$${{S}_{1}}$$表示$${{0}}$$到$${{t}_{1}}$$时间内$${{A}}$$的$${{a}{−}{t}}$$图线与坐标轴所围面积大小，$${{S}_{2}}$$、$${{S}_{3}}$$分别表示$${{t}_{1}}$$到$${{t}_{3}}$$时间内$${{A}}$$、$${{B}}$$的$${{a}{−}{t}}$$图线与坐标轴所围面积大小。下列说法正确的是$${{(}{)}}$$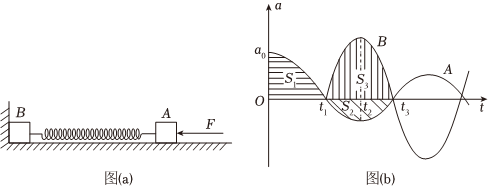
A.$${{0}}$$到$${{t}_{1}}$$时间内，墙对$${{B}}$$的冲量小于$${{m}_{A}{{S}_{1}}}$$
B.$${{m}_{B}{>}{{m}_{A}}}$$
C.$${{B}}$$运动后，弹簧的最大形变量等于$${{x}}$$
D.$${\frac{S_{1}} {S_{2}}}={\frac{m_{A}+m_{B}} {2 m_{B}}}$$
7、['机械能守恒定律'， '动量定理内容及应用'， '对动量守恒条件的理解']正确率80.0%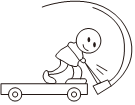
课后同学们都在讨论上周的高考题，说现在的题目是越来越灵活了，我们还要更加努力才行！如图所示，在光滑的地面上，人、车、锤一起向右在做匀速直线运动，不计空气阻力，下列说法正确的是$${{(}{)}}$$
A.车上的人用锤连续敲打小车可以使小车停止运动
B.人、车、锤组成的系统机械能守恒，系统动量也守恒
C.人、车、锤组成的系统机械能不守恒，系统水平方向动量守恒
D.人、车、锤组成的系统机械能不守恒，用锤敲打小车时锤给车的冲量大于车给锤的冲量
8、['机械能守恒定律'， '对动量守恒条件的理解']正确率80.0%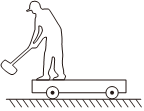
如图所示，在光滑的水平面上有一辆平板车。开始时人、锤和车都处于静止状态。人站在车左端，且始终与车保持相对静止，人抡起锤敲打车的左端，每当锤打到车左端时都立即与车具有共同速度。在连续的敲打的过程中，下列说法正确的是$${{(}{)}}$$
A.小车将持续地向右运动
B.锤、人和车组成的系统机械能守恒
C.每次锤被向左抡到最高点的时刻，人和车的速度都向右
D.每当锤打到车左端的时刻，人和车立即停止运动
9、['对动量守恒条件的理解']正确率80.0%质量相同的甲、乙两人站在光滑的冰面上，甲的手中拿有一个球，甲将球抛给乙，乙接到后，又抛给甲，如此反复多次，最后球落在乙手中。此时甲、乙两人的速率关系是$${{(}{)}}$$
A.甲、乙两人速率相等
B.甲速率大
C.乙速率大
D.两人仍保持静止状态
10、['对动量守恒条件的理解']正确率40.0%人和气球离地高度为$${{h}}$$，恰好悬浮在空中，气球质量为$${{M}}$$，人的质量为$${{m}}$$，人要从气球下拴着的软绳上安全的下滑到地面，软绳的长度至少为多少？$${{(}{)}}$$
C
A.$$\frac{M h} {M+m}$$
B.$$\frac{m h} {M+m}$$
C.$$\frac{( m+M ) h} {M}$$
D.$$\frac{( m+M ) h} {m}$$
1. 解析：根据题目描述，光子被反射时冲量为$$2p$$，被吸收时冲量为$$p$$。薄膜的反光率为$$η$$，因此反射的光子占比为$$η$$，吸收的光子占比为$$1-η$$。单位时间内单位面积上的光子总冲量为$$(1+η)p$$。太阳光的辐射功率为$$P_0$$，光子的能量$$E=pc$$，因此单位时间单位面积上的光子动量$$p=\frac{P_0}{c}$$。总冲量$$F=(1+η)\frac{P_0}{c}S$$，加速度$$a=\frac{F}{m}=\frac{(1+η)P_0S}{cm}$$。正确答案是选项B。
3. 解析：小球下滑过程中，系统水平方向不受外力，动量守恒；但竖直方向有重力作用，动量不守恒。小球和槽的相互作用力做功，因为槽会移动。系统机械能守恒，但小球被弹簧反弹后，由于弹簧的弹性势能，小球不能回到原高度。选项D正确。
5. 解析：小球从A到C过程中，系统水平方向动量守恒，机械能守恒。由于$$m 7. 解析：系统水平方向不受外力，动量守恒；敲打小车时机械能不守恒（有内能产生），选项C正确。用锤敲打小车时，锤和车的冲量大小相等，选项D错误。 9. 解析：抛接球过程中系统动量守恒。最终球在乙手中，说明乙获得更多动量，因此乙的速率更大，选项C正确。