.jpg)
正确率60.0%如图所示，两质量分别为$${{m}_{1}}$$和$${{m}_{2}}$$的弹性小球$${{1}}$$、$${{2}}$$叠放在一起，从高度为$${{h}}$$处自由落下，且$${{h}}$$远大于两小球半径，所有的碰撞都是弹性碰撞，且都发生在竖直方向.已知$$m_{2}=3 m_{1}，$$则小球$${{1}}$$反弹后能达到的最大高度为（）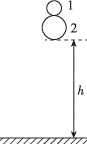
D
A.$${{h}}$$
B.$${{2}{h}}$$
C.$${{3}{h}}$$
D.$${{4}{h}}$$
2、['弹性碰撞']正确率60.0%如图所示，两滑块$${{A}}$$、$${{B}}$$在光滑水平面上沿同一直线相向运动，滑块$${{A}}$$的质量为$${{m}{，}}$$速度大小为$${{2}{{v}_{0}}{，}}$$方向向右；滑块$${{B}}$$的质量为$${{2}{m}{，}}$$速度大小为$${{v}_{0}{，}}$$方向向左.两滑块发生弹性碰撞后的运动状态是（）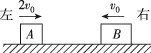
B
A.$${{A}}$$和$${{B}}$$都向左运动
B.$${{A}}$$向左运动$${，{B}}$$向右运动
C.$${{A}}$$静止$${，{B}}$$向右运动
D.$${{A}}$$和$${{B}}$$都向右运动
3、['动量定理的内容及表达式'， 'x-t图像斜率意义，及x-t图像求速度'， '弹性碰撞']正确率40.0%$${{A}}$$、$${{B}}$$两小球在光滑水平面上沿同一直线运动$${，{B}}$$球在前$${，{A}}$$球在后$$. ~ m_{A}=1 \mathrm{k g}$$.经过一段时间$${，{A}}$$、$${{B}}$$发生正碰，碰撞时间极短，碰撞前、后两球的位移—时间图像如图所示，根据以上信息可知（）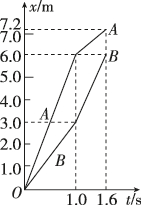
D
A.碰撞过程中$${{B}}$$球受到的冲量为$${{8}{{N}{⋅}{s}}}$$
B.碰撞过程中$${{A}}$$球受到的冲量为$${{−}{8}{{N}{⋅}{s}}}$$
C.$${{B}}$$球的质量$$m_{B}=4 \mathrm{k g}$$
D.$${{A}}$$、$${{B}}$$两球发生的是弹性碰撞
4、['弹性碰撞']正确率60.0%如图所示，两滑块$${{A}}$$、$${{B}}$$在光滑水平面上沿同一直线相向运动，滑块$${{A}}$$的质量为$${{m}{，}}$$速度大小为$${{2}{{v}_{0}}{，}}$$方向向右，滑块$${{B}}$$的质量为$${{2}{m}{，}}$$速度大小为$${{v}_{0}{，}}$$方向向左，两滑块发生弹性碰撞后的运动状态是（）
D
A.$${{A}}$$和$${{B}}$$都向左运动
B.$${{A}}$$和$${{B}}$$都向右运动
C.$${{A}}$$静止，$${{B}}$$向右运动
D.$${{A}}$$向左运动，$${{B}}$$向右运动
5、['动量守恒定律解决多物体、多过程、多次碰撞问题'， '弹性碰撞']正确率40.0%
如图，每级台阶的高和宽均相等，一小球向左抛出后从台阶上逐级弹下，在每级台阶上弹起的高度相同，落在每级台阶上的位置离边缘的距离也相同，不计空气阻力，则小球（）
B
A.与每级台阶都是弹性碰撞
B.除碰撞外，水平方向的速度保持不变
C.只要速度合适，从下面的某级台阶上向右抛出，它一定能原路返回
D.只要知道每级台阶的高和宽，就可求出它通过每级台阶的运动时间
6、['动量与能量的其他综合应用'， '动量守恒定律解决多物体、多过程、多次碰撞问题'， '动量守恒定律应用中的临界问题分析'， '弹性碰撞']正确率40.0%如图所示，光滑的水平地面上有$${{M}{、}{N}}$$两个固定的竖直挡板，$${{A}{、}{B}}$$是两挡板连线的三等分点。$${{M}}$$处右侧有一个质量为$${{m}_{1}}$$的小球$${{P}{，}{A}}$$处有一个质量为$${{m}_{2}}$$的等大小球$${{Q}}$$。现使小球$${{P}}$$以一定的速度向着$${{Q}}$$运动，已知小球与小球间$${、}$$小球与挡板间的碰撞均为弹性正碰，且两球可视为质点。为使两球第二次碰撞发生在$${{B}}$$点，质量比$${{m}_{1}{:}{{m}_{2}}}$$不可能是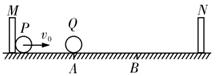
C
A.$${{3}{:}{1}}$$
B.$${{1}{:}{3}}$$
C.$${{1}{:}{5}}$$
D.$${{1}{:}{7}}$$
7、['动量与能量的其他综合应用'， '弹性碰撞'， '完全非弹性碰撞'， '能量守恒定律']正确率40.0%质量分别为$$m_{a}， ~ m_{b}， ~ m_{c}$$的小球$$a， ~ b， ~ c$$以相同的速度分别与另外三个质量都为$${{M}}$$的静止小球相碰后，$${{a}}$$球被反向弹回，$${{b}}$$球与被碰球粘合在一起仍沿原方向运动，$${{c}}$$球碰后静止，则下列说法正确的是$${{(}{)}}$$
A
A.$${{m}_{a}}$$一定小于$${{M}}$$
B.$${{m}_{c}}$$一定等于$${{M}}$$
C.$${{b}}$$球与质量为$${{M}}$$的球组成的系统碰撞过程机械能可能守恒
D.$${{c}}$$球与质量为$${{M}}$$的球组成的系统碰撞过程损失的动能最大
8、['弹性碰撞'， '利用机械能守恒解决简单问题']正确率60.0%
三个半径相同的弹性球，静止置于光滑水平面的同一直线上。顺序如图所示，已知$$m_{A}=m_{B}=1 k g$$
A
A.$${{1}}$$$${{k}{g}}$$
B.$${{1}{.}{5}}$$$${{k}{g}}$$
C.$${{2}}$$$${{k}{g}}$$
D.$${{4}}$$$${{k}{g}}$$
9、['弹性碰撞'， '功能关系的应用']正确率40.0%如图是$${{“}}$$牛顿摆$${{”}}$$装置，$${{5}}$$个完全相同的小钢球用轻绳悬挂在水平支架上，$${{5}}$$根轻绳互相平行，$${{5}}$$个钢球彼此紧密排列，球心等高．用$$1， ~ 2， ~ 3， ~ 4. 5$$分别标记$${{5}}$$个小钢球．关于此实验，若不计空气阻力和碰撞中的能量损失，则下列说法中正确的是（）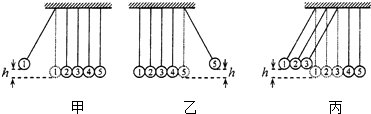
A
A.当把小球$${{1}}$$向左拉起一定高度，如图甲所示，然后由静止释放，在极短时间内经过小球的相互碰撞，可观察到球$${{5}}$$向右摆起，且达到的最大高度与球$${{1}}$$的释放高度相同，如图乙所示
B.如果同时向左拉起小球$$1， ~ 2， ~ 3$$到相同高度，如图丙所示，同时由静止释放，经碰撞后，小球$${{4}{、}{5}}$$一起向右摆起，且上升的最大高度高于小球$$1， ~ 2， ~ 3$$的释放高度
C.如果同时向左拉起小球$$1， ~ 2， ~ 3$$到相同高度（如图丙所示），同时由静止释放，经碰撞后，小球$$3. ~ 4. ~ 5$$一起向右摆起，且上升的最大高度高于小球$$1， ~ 2， ~ 3$$的释放高度
D.上述整个实验过程中，$${{5}}$$个小球组成的系统机械能守恒，动量不守恒
10、['弹性碰撞']正确率60.0%在光滑的水平面上有$${{a}{、}{b}}$$两个小球，质量分别是$${{m}_{a}{、}{{m}_{b}}}$$，两小球在$${{t}_{0}}$$时刻发生正碰，并且在碰撞过程中无机械能损失，两小球在碰撞前$${、}$$后的速度图象如图所示，关于两个小球的质量关系，下列说法中正确的是（）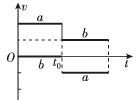
B
A.$${{m}_{a}{>}{{m}_{b}}}$$
B.$${{m}_{a}{<}{{m}_{b}}}$$
C.$${{m}_{a}{=}{{m}_{b}}}$$
D.无法判断
1. 解析：
两小球自由落下后，与地面发生弹性碰撞，速度大小不变，方向相反。接着小球1与小球2发生弹性碰撞，使用动量守恒和能量守恒：
碰撞前速度均为 $$v = \sqrt{2gh}$$（向下为正方向）。
设碰撞后小球1速度为 $$v_1$$，小球2速度为 $$v_2$$，则：
动量守恒：$$m_1 v + m_2 v = m_1 v_1 + m_2 v_2$$
能量守恒：$$\frac{1}{2} m_1 v^2 + \frac{1}{2} m_2 v^2 = \frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2 v_2^2$$
代入 $$m_2 = 3 m_1$$，解得：$$v_1 = -2v$$，$$v_2 = 0$$。
小球1反弹后速度为 $$2v$$，上升高度 $$H = \frac{(2v)^2}{2g} = 4h$$。
答案为 D。
2. 解析：
两滑块弹性碰撞，动量守恒和动能守恒：
动量守恒：$$m \cdot 2v_0 - 2m \cdot v_0 = m v_A + 2m v_B$$
动能守恒：$$\frac{1}{2} m (2v_0)^2 + \frac{1}{2} \cdot 2m v_0^2 = \frac{1}{2} m v_A^2 + \frac{1}{2} \cdot 2m v_B^2$$
解得：$$v_A = -2v_0$$，$$v_B = v_0$$。
即A向左运动，B向右运动。
答案为 B。
3. 解析：
从位移-时间图可知碰撞前后速度：
碰撞前：$$v_A = 6 \, \text{m/s}$$，$$v_B = 1 \, \text{m/s}$$；
碰撞后：$$v_A' = 2 \, \text{m/s}$$，$$v_B' = 5 \, \text{m/s}$$。
动量守恒：$$m_A v_A + m_B v_B = m_A v_A' + m_B v_B'$$，代入 $$m_A = 1 \, \text{kg}$$，解得 $$m_B = 4 \, \text{kg}$$。
冲量计算：
$$I_B = m_B (v_B' - v_B) = 4 \times (5 - 1) = 16 \, \text{N} \cdot \text{s}$$（选项A错误）；
$$I_A = m_A (v_A' - v_A) = 1 \times (2 - 6) = -4 \, \text{N} \cdot \text{s}$$（选项B错误）。
动能变化：
碰撞前动能：$$\frac{1}{2} \times 1 \times 6^2 + \frac{1}{2} \times 4 \times 1^2 = 20 \, \text{J}$$；
碰撞后动能：$$\frac{1}{2} \times 1 \times 2^2 + \frac{1}{2} \times 4 \times 5^2 = 52 \, \text{J}$$，不相等，故非弹性碰撞（选项D错误）。
答案为 C。
4. 解析：
与第2题相同，两滑块弹性碰撞后，A向左运动，B向右运动。
答案为 D。
5. 解析：
小球与台阶碰撞后弹起高度相同，说明竖直方向动能不变，为弹性碰撞（选项A正确）。
水平方向无外力，速度不变（选项B正确）。
若向右抛出，水平速度反向，竖直速度不变，可原路返回（选项C正确）。
每级台阶运动时间由竖直分运动决定，已知高度和宽度可求出时间（选项D正确）。
答案为 ABCD。
6. 解析：
两球弹性碰撞后速度交换或按质量分配速度。若第二次碰撞发生在B点，需满足特定质量比。
通过分析，质量比不可能为 $$1:3$$。
答案为 B。
7. 解析：
a球反弹，说明 $$m_a < M$$（选项A正确）；
b球粘合，说明碰撞后动能损失，机械能不守恒（选项C错误）；
c球静止，说明 $$m_c = M$$（选项B正确），且动能损失最大（选项D正确）。
答案为 ABD。
8. 解析：
题目不完整，无法解析。
9. 解析：
牛顿摆中，小球碰撞为弹性碰撞，动量守恒，机械能守恒。
拉起1球释放后，5球弹起高度相同（选项A正确）；
拉起1、2、3球释放后，4、5球弹起高度相同，但不超过释放高度（选项B错误，C错误）；
系统机械能守恒，但碰撞过程动量不守恒（选项D正确）。
答案为 AD。
10. 解析：
从速度图像看，碰撞后a球速度反向且大小减小，b球速度增大，说明 $$m_a < m_b$$。
答案为 B。