.jpg)
正确率60.0%以下对碰撞的理解，说法正确的是（）
C
A.弹性碰撞一定是对心碰撞
B.非对心碰撞一定是非弹性碰撞
C.弹性碰撞也可能是非对心碰撞
D.弹性碰撞和对心碰撞中动量守恒，非弹性碰撞和非对心碰撞中动量不守恒
2、['碰撞']正确率80.0%两个完全相同的小球在光滑水平面上沿同一直线运动，$${{A}}$$球速度是$${{6}{m}{/}{s}}$$，$${{B}}$$球速度是$${{4}{m}{/}{s}}$$，$${{A}}$$球追上$${{B}}$$球时发生碰撞，则碰撞后$${{A}}$$、$${{B}}$$两球的速度可能值是$${{(}{)}}$$
A.$$v_{A}=5. 5 m / s$$，$$v_{B}=4. 5 m / s$$
B.$$v_{A}=4. 5 m / s$$，$$v_{B}=5. 5 m / s$$
C.$$v_{A}=3. 8 m / s$$，$$v_{B}=6. 2 m / s$$
D.$$v_{A}=-2 m / s$$，$$v_{B}=1 2 m / s$$
3、['动量定理的定量计算'， '碰撞']正确率60.0%
所谓对接是指两艘同方向以几乎同样快慢运行的宇宙飞船在太空中互相靠近，最后连接在一起。假设$${{“}}$$
C
A.$$\frac{m^{2} \cdot\triangle v} {( M+m ) \triangle t}$$
B.$$\frac{M^{2} \cdot\triangle v} {( M+m ) \triangle t}$$
C.$$\frac{M m \cdot\triangle v} {( M+m ) \triangle t}$$
D.$${{0}}$$
4、['碰撞']正确率40.0%
如图所示，光滑水平面上有大小相同的$${{A}{、}{B}}$$
B
A.左方是$${{A}}$$球，碰撞后$${{A}{、}{B}}$$两球速度大小之比为$${{2}{：}{5}}$$
B.左方是$${{A}}$$球，碰撞后$${{A}{、}{B}}$$两球速度大小之比为$${{1}{：}{{1}{0}}}$$
C.右方是$${{A}}$$球，碰撞后$${{A}{、}{B}}$$两球速度大小之比为$${{1}{：}{{1}{0}}}$$
D.右方是$${{A}}$$球，碰撞后$${{A}{、}{B}}$$两球速度大小之比为$${{2}{：}{5}}$$
5、['碰撞']正确率40.0%甲$${、}$$乙两球在光滑水平轨道上同向运动，已知它们的动量分别是$$p_{\#}=5 ~ k g \cdot m / s， ~ p_{Z}=7 ~ k g \cdot m / s$$，甲追乙并发生碰撞，碰后乙球的动量变为$$p_{z}^{\prime}=1 0 ~ k g \cdot m / s$$，则关于甲球动量的大小和方向判断正确的是（）
B
A.$$p_{\tiny\mathrm{\#}}^{\prime}=2 k g \cdot m / s$$，方向与原来方向相反
B.$$p_{\tiny\mathrm{\#}}^{\prime}=2 k g \cdot m / s$$，方向与原来方向相同
C.$$p_{\mp}^{\prime}=4 ~ k g \cdot m / s$$，方向与原来方向相反
D.$$p_{\mp}^{\prime}=4 ~ k g \cdot m / s$$，方向与原来方向相同
6、['碰撞'， '能量守恒定律']正确率40.0%两个质量相等的小球在光滑水平面上沿同一直线同方向运动，$${{A}}$$球的动量是$$8 \mathrm{k g} \cdot\mathrm{m / s}， \ B$$球的动量是$$5 \， \mathrm{k g} \! \cdot\mathrm{m / s}， \ A$$球追上$${{B}}$$球时发生碰撞，则碰撞后$${{A}{、}{B}}$$两球的动量可能值是（）
C
A.$$p_{A}=-2$$$$\mathrm{k g \cdot m / s， ~} ~ P_{B}=1 4$$$$\mathrm{k g \cdot m / s}$$
B.$${{p}_{A}{=}{3}}$$$$\mathrm{k g \cdot m / s， ~} ~ P_{B}=1 0$$$$\mathrm{k g \cdot m / s}$$
C.$${{p}_{A}{=}{6}}$$$$\mathrm{k g \cdot m / s}， ~ P_{B}=7$$$$\mathrm{k g \cdot m / s}$$
D.$$p_{A}=9 \mathrm{k g} \cdot\mathrm{m / s}， ~ P_{B}=4 \mathrm{k g} \cdot\mathrm{m / s}$$
7、['碰撞'， '库仑力作用下的动力学问题']正确率40.0%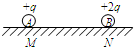
如图所示，在光滑绝缘水平面上的$${{M}{、}{N}}$$
A
A.$$E_{1}=E_{2} > E， \， \， P_{1}=P_{2} > P$$
B.$$E_{1}=E_{2}=E， \， \， P_{1}=P_{2}=P$$
C.碰撞一定发生在$${{M}{、}{N}}$$连线中点的左侧
D.两球不可能同时返回到$${{M}{、}{N}}$$两点
8、['碰撞'， '动量及动量变化'， '牛顿第二定律的简单应用']正确率60.0%两球在光滑的水平面上相向运动，发生正碰后，两球均静止，由此可知两球在碰撞前一定有$${{(}{)}}$$
B
A.大小相等的反向速度
B.大小相等的反向动量
C.相等的质量
D.大小相等的反向加速度
9、['碰撞'， '判断系统机械能是否守恒'， '弹簧类机械能转化问题']正确率40.0%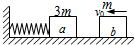
如图所示，在光滑水平面上，有质量分别为$${{3}{m}}$$
C
A.$$\frac{m v_{0}^{2}} {2}$$
B.$$\frac{m v_{0}^{2}} {4}$$
C.$$\frac{m v_{0}^{2}} {8}$$
D.$$\frac{m v_{0}^{2}} {1 6}$$
10、['碰撞'， '完全非弹性碰撞']正确率40.0%半径相等的两个小球甲和乙，在光滑的水平面上沿同一直线相向运动，若甲球质量大于乙球质量，发生碰撞前，两球的动能相等，则碰撞后两球的状态可能是$${{(}{)}}$$
C
A.两球的速度方向均与原方向相反，但它们动能仍相等
B.两球的速度方向相同，而且它们动能仍相等
C.甲、乙两球的动量相同
D.甲球的动量不为零，乙球的动量为零
1. 解析：
2. 解析：
- 选项A：$$5.5m + 4.5m = 10m$$（动量守恒），动能 $$(5.5^2 + 4.5^2)m/2 = 25.25m$$，初始动能 $$(6^2 + 4^2)m/2 = 26m$$，合理。
- 选项B：$$4.5m + 5.5m = 10m$$（动量守恒），动能 $$(4.5^2 + 5.5^2)m/2 = 25.25m$$，合理。
- 选项C：$$3.8m + 6.2m = 10m$$（动量守恒），动能 $$(3.8^2 + 6.2^2)m/2 = 26.44m$$，大于初始动能，不合理。
- 选项D：$$-2m + 12m = 10m$$（动量守恒），动能 $$(2^2 + 12^2)m/2 = 74m$$，远大于初始动能，不合理。
3. 解析：
4. 解析：
- 若左方是 $$A$$ 球，碰撞后 $$v_A : v_B = 2 : 5$$，可能满足动量守恒 $$m_A v_A + m_B v_B = m_A u_A + m_B u_B$$。
- 若右方是 $$A$$ 球，碰撞后 $$v_A : v_B = 1 : 10$$，可能满足动量守恒。
5. 解析：
- 初始动能：$$\frac{5^2}{2m} + \frac{7^2}{2m} = \frac{74}{2m}$$。
- 碰后动能：$$\frac{2^2}{2m} + \frac{10^2}{2m} = \frac{104}{2m}$$，大于初始动能，不合理。
6. 解析：
- 选项A：$$-2 + 14 = 12$$（不守恒），排除。
- 选项B：$$3 + 10 = 13$$（守恒），动能 $$\frac{3^2}{2m} + \frac{10^2}{2m} = \frac{109}{2m}$$，大于初始动能，排除。
- 选项C：$$6 + 7 = 13$$（守恒），动能 $$\frac{6^2}{2m} + \frac{7^2}{2m} = \frac{85}{2m}$$，小于初始动能，合理。
- 选项D：$$9 + 4 = 13$$（守恒），动能 $$\frac{9^2}{2m} + \frac{4^2}{2m} = \frac{97}{2m}$$，大于初始动能，排除。
7. 解析：
8. 解析：
9. 解析：
- 动量守恒：$$3m v_0 = 3m v_1 + m v_2$$。
- 动能守恒：$$\frac{1}{2} 3m v_0^2 = \frac{1}{2} 3m v_1^2 + \frac{1}{2} m v_2^2$$。
10. 解析：
- 若两球速度反向且动能相等，可能满足动量守恒。
- 若两球速度同向，动能可能不等。
- 甲球动量不为零、乙球动量为零可能满足动量守恒。