.jpg)
正确率80.0%质量为$${{m}}$$，速度为$${{v}}$$的$${{A}}$$球跟质量为$${{3}{m}}$$的静止的$${{B}}$$球发生正碰．碰撞可能是弹性的，也可能是非弹性的，因此碰撞后$${{B}}$$球的速度可能值为$${{(}{)}}$$
A.$${{0}{.}{6}{v}}$$
B.$${{0}{.}{4}{v}}$$
C.$${{0}{.}{2}{v}}$$
D.$${{0}{.}{1}{v}}$$
2、['动量与能量的其他综合应用'， '碰撞'， '弹性碰撞']正确率40.0%内壁光滑的圆环管道固定于水平面上，图为水平面的俯视图$${{.}{O}}$$为圆环圆心，直径略小于管道内径的甲、乙两个等大的小球(均可视为质点)分别静置于$${{P}}$$、$${{Q}}$$处$$， \， \， P O \perp O Q，$$甲、乙两球质量分别为$${{k}{m}}$$、$${{m}}$$.现给甲球一瞬时冲量，使甲球沿图示方向运动，甲、乙两球发生弹性碰撞，碰撞时间不计，碰后甲球立即反弹，甲球刚到$${{P}^{′}}$$处时，恰好与乙球再次发生碰撞，则（）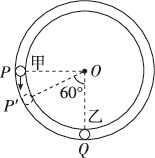
B
A.$$k=\frac{7} {5}$$
B.$$k=\frac{5} {7}$$
C.$$k=\frac{5} {3}$$
D.$$k=\frac{3} {5}$$
3、['动量守恒-系统在某一方向不受力'， '弹性碰撞'， '机械能与曲线运动结合问题']正确率40.0%如图所示，在光滑水平面上放置一个质量为$${{m}}$$的滑块，滑块右侧面为一个半径为$${{R}}$$的$$\frac{1} {4}$$弧形的光滑凹槽，$${{A}}$$点切线水平。另有一个质量为$${{m}}$$的小球以水平速度$${{v}_{0}}$$从$${{A}}$$点冲上凹槽，重力加速度大小为$${{g}}$$。下列说法中正确的是（）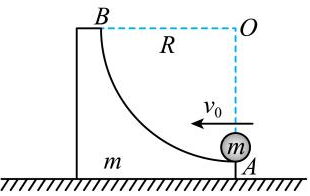
D
A.当$${{v}_{0}{=}{\sqrt {{2}{g}{R}}}}$$时，小球恰好能到达$${{B}}$$点
B.当$${{v}_{0}{=}{\sqrt {{2}{g}{R}}}}$$时，小球在弧形凹槽上冲向$${{B}}$$点的过程中，滑块的动能增大；返回$${{A}}$$点的过程中，滑块的动能减小
C.如果小球的速度$${{v}_{0}}$$足够大，球将从滑块的左侧离开滑块后落到水平面上
D.小球返回$${{A}}$$点后做自由落体运动
4、['弹性碰撞'， '动量定理内容及应用']正确率40.0%$${{A}}$$、$${{B}}$$两小球在光滑水平面上沿同一直线运动，$${{B}}$$球在前，$${{A}}$$球在后，$$m_{A}=1 k g$$。经过一段时间，$${{A}}$$、$${{B}}$$发生正碰，碰撞时间极短，碰撞前、后两球的位移$${{−}}$$时间图像如图所示，根据以上信息可知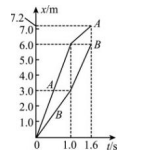
D
A.碰撞过程中$${{B}}$$球受到的冲量为$${{8}{N}{s}}$$
B.碰撞过程中$${{A}}$$球受到的冲量为$${{−}{8}{N}{s}}$$
C.$${{B}}$$球的质量$$m_{B}=4 k g$$
D.$${{A}{B}}$$两球发生的是弹性碰撞
5、['弹性碰撞']正确率40.0%$${{A}{、}{B}}$$两个小球在光滑水平面上沿同一条直线相向运动．已知$${{A}}$$球的动量大小为$$3 k g \cdot m / s， ~ B$$球的动量大小为$$5 k g \cdot m / s$$，两球发生对心正碰．下列说法正确的是（）
C
A.$${{A}}$$球的质量一定大于$${{B}}$$球的质量
B.若两球同向运动，碰撞前，$${{A}}$$球在前，$${{B}}$$球在后，则$${{A}}$$球的质量一定等于$${{B}}$$球的质量
C.碰撞后$${{A}{、}{B}}$$两球的总动量大小为$$2 k g \cdot m / s$$
D.碰撞后两球运动方向可能都与碰撞前$${{A}}$$球运动方向相同
6、['x-t图像斜率意义，及x-t图像求速度'， '弹性碰撞'， '动量及动量变化']正确率19.999999999999996%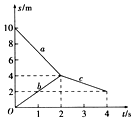
甲$${、}$$
C
A.碰撞前甲$${、}$$乙两物体的运动方向相同
B.碰撞后甲与乙结合体的速度大小是$$0. 5 m / s$$
C.甲$${、}$$乙两物体碰撞前的总动量大小为$$5 k g \cdot m / s$$
D.碰撞前后甲$${、}$$乙两物体组成的系统损失的动能为$${{1}{0}{J}}$$
7、['弹性碰撞'， '核反应']正确率40.0%某实验室工作人员，用初速度$$v_{0}=0. 0 9 c ( c$$为真空中的光速)的$${{α}}$$粒子轰击静止的氮原子核$$\stackrel{1 4} {7} \mathrm{N}$$，产生了质子$${^{1}_{1}{H}}$$.若某次碰撞可看作对心正碰，碰后新核与质子同方向运动，垂直磁场方向射入磁场，通过分析偏转半径可得出新核与质子的速度大小之比为$${{1}{∶}{{2}{0}}}$$，已知质子质量为$${{m}{.}}$$（）
B
A.该核反应方程$$\mathrm{^4 H e+^{1 4}_{7} \ N \to_{8}^{1 6} \ O}$$$${{+}{^{1}_{1}{H}}}$$
B.质子的速度$${{v}}$$为$$0. 2 0 c$$
C.若用两个上述质子发生对心弹性碰撞，则每个质子的动量变化量是$$0. 2 0 m c$$
D.若用两个上述质子发生对心弹性碰撞，则每个质子的动量变化量方向与末动量方向相反
8、['动量守恒定律解决多物体、多过程、多次碰撞问题'， '弹性碰撞'， '利用机械能守恒解决简单问题']正确率60.0%如图所示，立柱固定于光滑水平面上$${{O}}$$点，质量为$${{M}}$$的小球$${{a}}$$向右运动，与静止于$${{Q}}$$点的质量为$${{m}}$$的小球$${{b}}$$发生弹性碰撞，碰后$${{a}}$$球立即向左运动$${，{b}}$$球与立柱碰撞时能量不损失，所有碰撞时间均不计$${，{b}}$$球恰好在$${{P}}$$点追到$${{a}}$$球.已知$${{Q}}$$点为$${{O}{P}}$$中点，则$${{a}}$$、$${{b}}$$两球质量之比$${{M}}$$∶$${{m}}$$为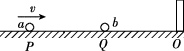
（）
A
A.$${{3}}$$∶$${{5}}$$
B.$${{1}}$$∶$${{3}}$$
C.$${{2}}$$∶$${{3}}$$
D.$${{1}}$$∶$${{2}}$$
9、['弹性碰撞']正确率40.0%质量为$${{2}{m}}$$的$${{B}}$$球，静止放于光滑水平面上，另一质量为$${{m}}$$的$${{A}}$$球以速度$${{v}}$$与$${{B}}$$球正碰，若碰撞没有能量损失，则碰后$${{A}}$$球的速度为$${{(}{)}}$$
B
A.$$\frac{v} {3}$$
B.$$- \frac{v} {3}$$
C.$$\frac{2 v} {3}$$
D.$$- \frac{2 v} {3}$$
10、['弹性碰撞'， 'v-t图像综合应用']正确率40.0%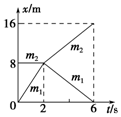
质量为$$m_{1}=1 k g$$
B
A.非弹性碰撞
B.弹性碰撞
C.完全非弹性碰撞
D.条件不足，不能确定
1、解析：
2、解析：