.jpg)
正确率40.0%质量为$${{m}{、}}$$速度为$${{v}}$$的$${{A}}$$球与质量为$${{3}{m}}$$的静止$${{B}}$$球发生正碰，碰撞后$${{B}}$$球的速度大小可能是（）
B
A.$${{0}{.}{6}{v}}$$
B.$${{0}{.}{4}{v}}$$
C.$${{0}{.}{2}{v}}$$
D.$${{v}}$$
2、['非完全弹性碰撞']正确率60.0%
在光滑的水平面上有两个在同一直线上相向运动的小球，其中甲球的质量$$m_{1}=2 k g$$
C
A.$$0. 5 m / s$$，向右
B.$$0. 5 m / s$$，向左
C.$$1. 5 m / s$$，向左
D.$$1. 5 m / s$$，向右
3、['弹性碰撞'， '非完全弹性碰撞']正确率40.0%质量为$${{1}{k}{g}}$$的小球$${{A}}$$以$$v_{0}=4 m / s$$的速度与质量为$${{3}{k}{g}}$$的静止小球$${{B}}$$发生正碰，碰后$${{A}}$$球速度为$${{v}_{1}{，}{B}}$$球速度为$${{v}_{2}}$$，关于$${{v}_{1}}$$和$${{v}_{2}}$$的数值中可能的是$${{(}{)}}$$
A
A.$$v_{1}=1 m / s$$$$v_{2}=1 m / s$$
B.$$v_{1}=2. 5 m / s$$$$v_{2}=0. 5 m / s$$
C.$$v_{1}=0. 5 m / s$$$$v_{2}=2 m / s$$
D.$$v_{1}=-5 m / s$$$$v_{2}=3 m / s$$
4、['计算物体动能的变化'， '动量守恒定律内容，应用范围和推导'， '功能关系的应用'， '非完全弹性碰撞']正确率40.0%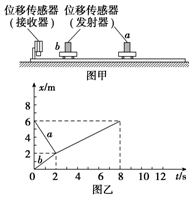
如图甲所示为某实验小组验证动量守恒定律的实验装置，他们将光滑的长木板固定在桌面上，$${{a}{、}{b}}$$
C
A.两车碰撞前总动量大于碰撞后总动量
B.碰撞过程中$${{a}}$$车损失的动能是$$\frac{1 4} {9} J$$
C.碰撞后两车的总动能比碰前的总动能小
D.两车碰撞过程为弹性碰撞
5、['非完全弹性碰撞']正确率40.0%甲球与乙球相碰，甲球的速度减少$${{5}{m}{/}{s}}$$，乙球的速度增加了$${{3}{m}{/}{s}}$$，则甲$${、}$$乙两球质量之比是（）
C
A.
B.
C.$$m_{\mp} \colon~ m_{\mp} ~=~ 3 \colon~ 5 ~$$
D.
正确率40.0%如图所示，距离地面高$${{h}}$$处固定着一光滑圆弧轨道，地面上有一个长为$${{3}{s}{、}}$$深度为$${{h}{、}}$$没有蓄水的长方体水池。水池的左边缘$${{C}}$$点与轨道底端$${{G}}$$的水平距离为$${{s}}$$。现将一个质量为$${{m}}$$的刚性小球乙放置在圆弧轨道边缘的$${{B}}$$点，再将一个与乙球形状完全相同$${、}$$质量为$${{M}}$$的小球甲从距$${{B}}$$点高度为$${{H}}$$的$${{A}}$$点由静止自由释放，甲球下滑到$${{B}}$$点与乙球发生正碰，碰后甲球刚好落到水池左边缘的$${{C}}$$点，乙球刚好落到水池右侧底端的$${{D}}$$点。如果$$H_{\smallsetminus} ~ h_{\nsim} ~ s$$的关系满足$$\sqrt{\mathrm{H h}} {\bf=} s，$$两个小球都可视为质点，则甲$${、}$$乙两球的质量之比$${{M}{：}{m}}$$为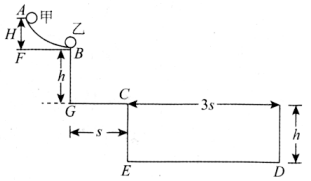
C
A.$${{2}}$$
B.$$\frac{1} {2}$$
C.$${{2}{\sqrt {2}}}$$
D.$${{1}{+}{\sqrt {2}}}$$
7、['非完全弹性碰撞']正确率40.0%在一次救灾行动中，需要把飞机上的$${{5}{0}}$$麻袋粮食投放到行驶的列车上，已知列车的质量为$${{M}}$$，列车在铁轨上以速度$${{v}_{0}}$$做匀速直线运动，列车上方的飞机也沿铁轨以速度$${{v}_{1}}$$同向匀速飞行.在某段时间内，飞机连续释放下$${{5}{0}}$$袋粮食，每袋粮食质量为$${{m}}$$，且这$${{5}{0}}$$袋粮食全部落在列车车厢内.不计列车与铁轨之间的摩擦，则列车载有粮食后的速度为（）
A
A.$$\frac{M v_{0}+5 0 m v_{1}} {M+5 0 m}$$
B.$${\frac{M v_{0}-5 0 M v_{1}} {M+5 0 m}}$$
C.$$\frac{M v_{0}} {M+5 0 m}$$
D.$$\frac{5 0 m v_{1}} {M+5 0 m}$$
8、['碰撞'， '非完全弹性碰撞']正确率40.0%质量为$${{2}{m}}$$的小球$${{A}}$$，在光滑的水平面上以速度$${{v}_{0}}$$与质量为$${{m}}$$的静止小球$${{B}}$$发生正碰，碰撞后$${{A}}$$球的动能恰变为原来的$$\frac{1} {9}，$$则$${{B}}$$球的速度大小可能是
C
A.$$\frac{1} {3}$$$${{v}_{0}}$$
B.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
C.$${\frac{4} {3}} v_{0}$$
D.$${\frac{8} {3}} v_{0}$$
9、['弹性碰撞'， '非完全弹性碰撞']正确率40.0%利用实验研究两个金属小球$${{a}{、}{b}}$$的碰撞。如图所示，将斜槽固定在平台上，使斜槽的末端水平。让质量较大的小球$${{a}}$$（入射小球）从斜槽上滚下，跟放在斜槽末端的大小相同$${、}$$质量较小的小球$${{b}}$$（被碰小球）发生正碰。将两个金属小球的碰撞视为弹性碰撞。下列说法正确的是（）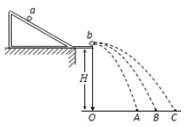
C
A.碰后小球$${{a}}$$的速度大于小球$${{b}}$$的速度
B.碰后小球$${{b}}$$的动量等于碰前小球$${{a}}$$的动量
C.只增大入射小球$${{a}}$$的质量，碰后两球落地点到$${{O}}$$的距离均增大
D.如果碰撞过程是非弹性碰撞，则碰撞过程两球动量不守恒
10、['动量与能量的其他综合应用'， '非完全弹性碰撞']正确率19.999999999999996%两个完全相同的小球$${{A}}$$、$${{B}}$$用长度均为$${{L}}$$的细线悬于天花板上，如图所示.若将$${{A}}$$从图示位置由静止释放，则$${{B}}$$球被碰后第一次速度为零时距离最低点的高度可能是（）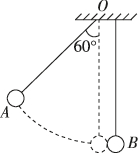
B
A.$$\frac{L} {9}$$
B.$$\frac{L} {5}$$
C.$$\frac{2 L} {3}$$
D.$$\frac{L} {1 0}$$
1. 根据动量守恒和能量关系分析碰撞问题：
动量守恒：$$mv = mv_A + 3mv_B$$
动能不增加：$$\frac{1}{2}mv^2 \geq \frac{1}{2}mv_A^2 + \frac{1}{2} \cdot 3mv_B^2$$
解得$$v_B \leq \frac{2v}{3}$$，且$$v_B \geq \frac{v}{2}$$（完全弹性碰撞时）。实际非弹性碰撞时$$v_B$$可能小于$$\frac{v}{2}$$，但需满足动能不增加。选项中$$0.4v$$符合要求，故选B。
2. 动量守恒问题：
设甲球初速$$v_1$$，乙球$$v_2$$，碰撞后甲球$$-0.5m/s$$（向左）。
动量守恒：$$2v_1 - v_2 = 2 \times (-0.5) + 1 \times 1.5$$
解得$$v_1 = 0.5m/s$$（向右），故选A。
3. 动量守恒和能量约束：
动量守恒：$$1 \times 4 = 1 \times v_1 + 3 \times v_2$$
动能不增加：$$\frac{1}{2} \times 1 \times 4^2 \geq \frac{1}{2} \times 1 \times v_1^2 + \frac{1}{2} \times 3 \times v_2^2$$
选项A满足动量守恒但动能增加（排除）；选项B动能不守恒；选项C满足所有条件；选项D动量守恒但动能增加（排除）。故选C。
4. 实验数据分析：
A错误，动量应守恒；B计算得$$a$$车动能损失$$\frac{14}{9}J$$正确；C正确，非弹性碰撞动能减少；D错误，动能不守恒。故选B、C。
5. 动量变化关系：
根据动量守恒：$$m_{\text{甲}} \times 5 = m_{\text{乙}} \times 3$$
解得质量比$$\frac{m_{\text{甲}}}{m_{\text{乙}}} = \frac{3}{5}$$，故选C。
6. 平抛运动与碰撞综合：
甲球碰后平抛时间$$t = \sqrt{\frac{2h}{g}}$$，水平位移$$s = v_{甲}t$$，得$$v_{甲} = \frac{s}{\sqrt{\frac{2h}{g}}}$$。
乙球位移$$3s = v_{乙}t$$，得$$v_{乙} = 3v_{甲}$$。
碰撞动量守恒：$$M\sqrt{2gH} = Mv_{甲} + m v_{乙}$$，代入$$v_{乙} = 3v_{甲}$$及$$\sqrt{Hh} = s$$，解得$$\frac{M}{m} = 2$$，故选A。
7. 连续投放动量问题：
系统动量守恒：$$Mv_0 + 50m v_1 = (M + 50m)v$$
解得$$v = \frac{Mv_0 + 50m v_1}{M + 50m}$$，故选A。
8. 动能变化与碰撞：
碰后A球动能$$\frac{1}{9} \times \frac{1}{2} \times 2m v_0^2$$，得速度$$v_A = \pm \frac{v_0}{3}$$。
动量守恒：$$2m v_0 = 2m \cdot \frac{v_0}{3} + m v_B$$或$$2m v_0 = 2m \cdot (-\frac{v_0}{3}) + m v_B$$
解得$$v_B = \frac{4v_0}{3}$$（合理）或$$\frac{8v_0}{3}$$（动能超限舍去），故选C。
9. 弹性碰撞特性：
A错误，a球质量大时碰后速度小于b球；B错误，动量守恒但b球动量小于a球初动量；C正确，增大a球质量会增大b球速度；D错误，动量始终守恒。故选C。
10. 完全非弹性碰撞情形：
A球下落至最低点速度$$v = \sqrt{2gL}$$，与B球碰撞后可能共速$$v' = \frac{v}{2}$$。
B球上升高度$$h = \frac{v'^2}{2g} = \frac{L}{4}$$（无此选项），或完全弹性碰撞时B球速度$$v$$，高度$$L$$（不符）。部分非弹性碰撞可能使高度为$$\frac{L}{9}$$，故选A。