.jpg)
正确率80.0%两个互相垂直的力$${{F}_{1}}$$和$${{F}_{2}}$$作用在同一物体上，使物体运动一段位移，此过程中$${{F}_{1}}$$对物体做功$${{2}{4}{J}}$$，物体克服$${{F}_{2}}$$做功$${{8}{J}}$$，再无其他力对物体做功，则物体的动能变化是（）
A
A.增加$${{1}{6}{J}}$$
B.减少$${{1}{6}{J}}$$
C.增加$${{3}{2}{J}}$$
D.减少$${{3}{2}{J}}$$
2、['计算物体动能的变化'， '水平面内的圆周运动'， '判断系统机械能是否守恒'， '用绳关联的多体机械能守恒问题'， '牛顿第二定律的简单应用']正确率40.0%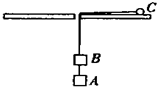
如图所示，在光滑的水平板的中央有一光滑的小孔，一根不可伸长的轻绳穿过小孔．绳的两端分别拴有一小球$${{C}}$$
D
A.剪断连接$${{A}{、}{B}}$$的绳子后，$${{B}}$$和$${{C}}$$组成的系统机械能增加
B.剪断连接$${{A}{、}{B}}$$的绳子后，小球$${{C}}$$的机械能不变
C.剪断连接$${{A}{、}{B}}$$的绳子后，物体$${{B}}$$对小球做功为$${{3}{m}{g}{R}}$$
D.剪断连接$${{A}{、}{B}}$$的绳子前，小球$${{C}}$$的动能为$${{2}{m}{g}{R}}$$
3、['计算物体动能的变化'， 'v-t图像面积意义，及v-t图像求位移'， 'v-t图像综合应用'， '机械能的概念及计算'， '重力做功']正确率40.0%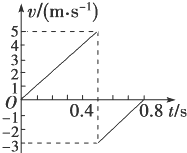
一质量为$${{1}{k}{g}}$$的小球从空中下落，与水平地面相碰后弹到空中某一高度，此过程的$${{v}{−}{t}}$$图象如图所示．若不计空气阻力，取$$g=1 0 m / s^{2}$$，则由图可知（）
C
A.小球从高度为$${{1}}$$$${{m}}$$处开始下落
B.小球在碰撞过程中损失的机械能为$${{4}{.}{5}}$$$${{J}}$$
C.小球能弹起的最大高度为$${{0}{.}{4}{5}}$$$${{m}}$$
D.整个过程中，小球克服重力做的功为$${{8}}$$$${{J}}$$
4、['计算物体动能的变化'， '力的方向与位移方向有夹角时的做功'， '摩擦力做功'， '动能定理的简单应用']正确率40.0%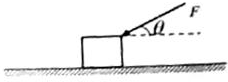
如图所示，质量为$${{m}}$$
C
A.推力$${{F}}$$做的功为$${{F}{S}{{s}{i}{n}}{θ}}$$
B.摩擦力做的功为$$- \mu m g S$$
C.合外力对物体做功为$$( \ F \operatorname{c o s} \theta-\mu m g-\mu F \operatorname{s i n} \theta) \enskip S$$
D.物体动能变化量为$$( \ F \operatorname{c o s} \theta-\mu m g ) \setminus S$$
5、['计算物体动能的变化'， '平抛运动基本规律及推论的应用'， '动能的定义及表达式'， '重力做功']正确率40.0%将一小球从高处水平抛出，最初$${{2}{s}}$$内小球动能$${{E}{k}}$$随时间$${{t}}$$变化的图象如图所示，不计空气阻力．根据上述信息，不能确定的物理量是$${{(}{g}}$$取$$1 0 ~ \mathrm{m / s^{2} )}$$（）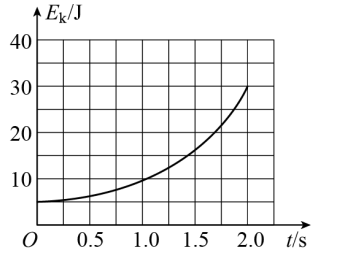
D
A.小球的质量
B.最初$${{2}{s}}$$内重力对小球做的功
C.小球抛出时的速度
D.小球抛出时离地面的高度
6、['计算物体动能的变化'， '动能定理和图像的综合问题'， 'v-t图像综合应用'， '动量及动量变化']正确率40.0%一质量为$${{2}{{k}{g}}}$$物体运动的速度随时间变化的关系如图所示，根据图象可知（）
D
A.$${{0}{∼}{4}{s}}$$内物体的速度方向保持不变
B.$${{0}{∼}{4}{s}}$$内合外力对物体做的功为零
C.物体加速度的方向在$${{2}{s}}$$时发生改变
D.$${{0}{∼}{4}{s}}$$内物体动量变化量的大小为$$\mathrm{1 6 k g \cdot m / s}$$
7、['计算物体动能的变化'， '重力做功与重力势能变化的关系'， '功能关系的应用']正确率60.0%如图所示，小孩荡秋千时，秋千摆动的最大幅度越来越小，则在秋千板下摆到最低点过程中$${{(}{)}}$$
B
A.小孩重力势能减小，动能不变，机械能减小
B.小孩重力势能减小，动能增加，机械能减小
C.小孩重力势能减小，动能增加，机械能增加
D.小孩重力势能减小，动能增加，机械能不变
8、['计算物体动能的变化'， '重力做功与重力势能变化的关系'， '机械能的概念及计算']正确率60.0%质量为$${{m}}$$的物体，由静止开始下落，由于空气阻力，下落的加速度为$${{4}{g}{/}{5}}$$，在物体下落$${{h}}$$的过程中，下列说法错误的是$${{(}{)}}$$
B
A.物体动能增加了$$4 m g h / 5$$
B.物体的机械能减少了$$4 m g h / 5$$
C.物体克服阻力所做的功为$$m g h / 5$$
D.物体的重力势能减少了$${{m}{g}}$$
9、['计算物体动能的变化'， '重力做功与重力势能变化的关系'， '摩擦力做功'， '动能定理的简单应用']正确率60.0%下列有关功和能量的说法，正确的是（）
D
A.摩擦力一定对物体做负功
B.某物体的速度发生了变化，则其动能一定发生变化
C.只要有力对物体做功，物体的动能一定发生变化
D.重力对物体做正功，物体的重力势能一定减少
10、['计算物体动能的变化'， '重力做功与重力势能变化的关系'， '验证机械能守恒定律']正确率60.0%
如图所示，$${{“}}$$
B
A.$$m g h < \frac1 2 m v^{2}$$
B.$$m g h=\frac{1} {2} m v^{2}$$
C.$$m g h < \frac1 4 m v^{2}$$
D.$$m g h=\frac{1} {4} m v^{2}$$
1. 解析：
根据动能定理，物体动能的变化等于合外力做的功。$${{F}_{1}}$$ 做功 $$24\text{J}$$，$${{F}_{2}}$$ 做负功 $$-8\text{J}$$（因为物体克服 $${{F}_{2}}$$ 做功）。合外力做功为 $$24\text{J} - 8\text{J} = 16\text{J}$$，因此动能增加 $$16\text{J}$$。正确答案是 A。
2. 解析：
剪断绳子后，$$B$$ 和 $$C$$ 组成的系统机械能守恒，但 $$C$$ 的机械能增加（因为 $$B$$ 对 $$C$$ 做功）。剪断前，$$C$$ 的动能为 $$2mgR$$（由圆周运动条件得出）。选项 D 正确。
3. 解析：
从 $$v-t$$ 图像可知：下落初速度 $$v_0=0$$，下落高度 $$h=\frac{1}{2}gt^2=1\text{m}$$（$$t=0.4\text{s}$$ 时落地）。反弹初速度 $$v=3\text{m/s}$$，最大高度 $$h'=\frac{v^2}{2g}=0.45\text{m}$$。碰撞损失机械能 $$\Delta E = \frac{1}{2}mv_0^2 - \frac{1}{2}mv^2 = 4.5\text{J}$$。选项 B 和 C 正确。
4. 解析：
推力 $$F$$ 做功为 $$FS\cos\theta$$，摩擦力做功为 $$-\mu(mg+F\sin\theta)S$$。合外力做功为 $$(F\cos\theta - \mu mg - \mu F\sin\theta)S$$，动能变化量等于合外力做功。选项 C 正确。
5. 解析：
由动能随时间变化的图像可求出初始动能 $$E_{k0}$$ 和 $$2\text{s}$$ 后的动能 $$E_{k}$$，从而确定质量 $$m$$ 和初速度 $$v_0$$。重力做功 $$W=mg\Delta h$$，但无法直接确定抛出高度 $$h$$（因下落时间未知）。不能确定的物理量是 D。
6. 解析：
$$0\sim4\text{s}$$ 内速度方向不变（始终为正），合外力做功为零（初末动能相同）。$$2\text{s}$$ 时加速度方向改变（斜率符号变化）。动量变化量 $$\Delta p = m\Delta v = 16\text{kg·m/s}$$。选项 A、B、D 正确。
7. 解析：
秋千摆动幅度减小说明机械能减小，但在最低点过程中重力势能转化为动能，因此动能增加。选项 B 正确。
8. 解析：
下落加速度 $$\frac{4}{5}g$$，阻力做功 $$-mgh/5$$。动能增加 $$\frac{4}{5}mgh$$，机械能减少 $$\frac{1}{5}mgh$$。重力势能减少 $$mgh$$。错误的选项是 B。
9. 解析：
摩擦力可以做正功（如传送带上的物体），速度方向变化时动能可能不变（如匀速圆周运动），合外力做功为零时动能不变。重力做正功时重力势能一定减少。正确答案是 D。
10. 解析：
由机械能守恒和动量守恒可得 $$mgh = \frac{1}{4}mv^2$$（因两物体质量相同，碰撞后速度减半）。选项 D 正确。