.jpg)
正确率60.0%关于摩擦力和作用力与反作用力做功的关系，下列说法正确的是（）
B
A.静摩擦力总是做正功，滑动摩擦力总是做负功
B.静摩擦力和滑动摩擦力都可能对物体不做功
C.作用力与反作用力所做的功一定大小相等
D.作用力做正功时，反作用力也一定做正功
2、['功能关系的应用'， '摩擦力做功'， '动能定理的简单应用']正确率40.0%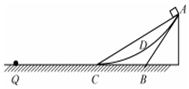
如图所示，斜面$$A B， ~ A C$$
B
A.$${{v}_{1}{<}{{v}_{2}}}$$
B.$${{v}_{2}{>}{{v}_{3}}}$$
C.$${{v}_{C}{=}{{v}^{′}_{C}}}$$
D.$${{v}_{B}{=}{{v}_{C}}}$$
3、['摩擦力做功'， '判断某个力是否做功，做何种功'， '功的定义、计算式和物理意义']正确率60.0%关于摩擦力和功，下列说法正确的是（）
B
A.静摩擦力总是做正功，滑动摩擦力总是做负功
B.静摩擦力和滑动摩擦力都可能对物体不做功
C.静摩擦力对物体一定做功，滑动摩擦力对物体可能不做功
D.静摩擦力对物体不一定做功，滑动摩擦力对物体一定做功
4、['用牛顿运动定律分析斜面体模型'， '摩擦力做功'， '动能定理的简单应用']正确率40.0%如图所示，质量为$$M=3 k g$$的小滑块，从斜面顶点$${{A}}$$由静止沿$${{A}{B}{C}}$$下滑，最后停在水平面上的$${{D}}$$点，不计滑块从$${{A}{B}}$$面滑上$${{B}{C}}$$面以及从$${{B}{C}}$$面滑上$${{C}{D}}$$面时的机械能损失。已知$$A B=B C=5 m， \， \， \， C D=9 m， \， \， \， \theta=5 3^{\circ}， \， \， \， \beta=3 7^{\circ} ( \operatorname{s i n} 3 7^{\circ}=0. 6， \operatorname{c o s} 3 7^{\circ}=0. 8$$，取重力加速度$$g=1 0 m / s^{2} )$$，在运动过程中，小滑块与所有接触面间的动摩擦因数相同。则（）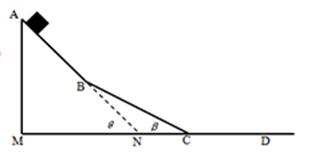
D
A.小滑块与接触面的动摩擦因数$${{μ}{=}{{0}{.}{5}}}$$
B.小滑块在$${{A}{B}}$$面上运动的加速度$${{a}_{1}}$$与小滑块在$${{B}{C}}$$面上的运动的加速度$${{a}_{2}}$$之比$$\frac{a_{1}} {a_{2}}=\frac{5} {3}$$
C.小滑块在$${{A}{B}}$$面上运动时间小于小滑块在$${{B}{C}}$$面上的运动时间
D.小滑块在$${{A}{B}}$$面上运动时克服摩擦力做功小于小滑块在$${{B}{C}}$$面上运动克服摩擦力做功
5、['功能关系的应用'， '摩擦力做功'， '动能定理的简单应用'， '重力做功']正确率40.0%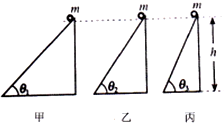
如图甲$${、}$$
B
A.到达斜底端时动能相同
B.各过程中重力做功大小相等
C.沿甲斜面下滑过程中重力做功最快
D.下滑相同高度时，沿丙斜面机械能损失最大
6、['匀变速直线运动的位移与时间的关系'， '牛顿第二定律的简单应用'， '摩擦力做功'， '功的定义、计算式和物理意义'， '动力学中的图像信息题']正确率40.0%如图甲所示，质量$$m=0. 5 ~ k g$$，初速度$$v_{0}=1 0 \， m / s$$的物体，受到一个与初速度方向相反的外力$${{F}}$$的作用，沿粗糙的水平面滑动，经$${{3}{s}}$$撤去外力，直到物体停止运动，整个过程物体的$${{v}{−}{t}}$$图象如图乙所示，取$$g=1 0 ~ m / s^{2}$$。下列说法不正确的是 （）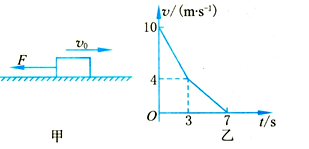
C
A.物体与地面的动摩擦因数为$${{0}{.}{1}}$$
B.$${{0}{∼}{2}{s}}$$内$${{F}}$$做的功为$${{−}{8}{J}}$$
C.$${{0}{∼}{7}{s}}$$内物体由于摩擦产生的热量为$${{2}{5}{J}}$$
D.$${{0}{∼}{7}{s}}$$内物体滑行的总位移为$${{2}{9}{m}}$$
7、['摩擦力做功']正确率40.0%
滑板运动是青少年喜爱的一项运动，一块滑板由板面滑板支架和四个轮子等部分组成．一位练习者踩着滑板在水平地面上向右匀速滑行，若练习者的脚受到的摩擦力为$${{f}_{1}}$$
B
A.$${{f}_{1}}$$做正功，$${{f}_{2}}$$做负功
B.$${{f}_{1}}$$做负功$${、{{f}_{2}}}$$做正功
C.$${{f}_{1}{、}{{f}_{2}}}$$均做正功
D.因为是静摩擦力，$${{f}_{1}{、}{{f}_{2}}}$$都不做功
8、['应用动能定理求变力做的功'， '摩擦力做功']正确率60.0%如图所示，固定在地面上的半圆轨道直径$${{a}{b}}$$水平，质点$${{P}}$$与半圆轨道的动摩擦因数处处一样，当质点$${{P}}$$从$${{a}}$$点正上方高$${{H}}$$处自由下落，经过轨道后从$${{b}}$$点冲出竖直上抛，上升的最大高度为$${{H}{/}{2}}$$，空气阻力不计．当质点下落再经过轨道$${{a}}$$点冲出时，能上升的最大高度$${{h}}$$为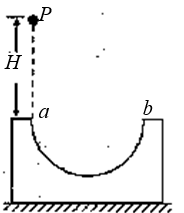
B
A.不能从$${{a}}$$点冲出半圆轨道
B.能从$${{a}}$$点冲出半圆轨道，但$$h ~ < ~ H / 2$$
C.能从$${{a}}$$点冲出半圆轨道，但$$h ~ > ~ H / 2$$
D.无法确定能否从$${{a}}$$点冲出半圆轨道
9、['平抛运动基本规律及推论的应用'， '平抛运动的概念和性质'， '滑动摩擦力大小'， '摩擦力做功'， '动能定理的简单应用']正确率60.0%如图所示，象棋子压着纸条，放在光滑水平桌面上.第一次沿水平方向将纸条抽出，棋子落在地面上的$${{P}}$$点.将棋子$${、}$$纸条放回原来的位置，仍沿原水平方向将纸条抽出，棋子落在地面上的$${{Q}}$$点，与第一次相比$${{(}{)}}$$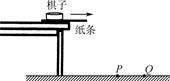
C
A.棋子受到纸条的摩擦力较大
B.棋子落地速度与水平方向夹角较大
C.纸条对棋子的摩擦力做功较多
D.棋子离开桌面至落地过程中动能增量较大
10、['匀变速直线运动的位移与时间的关系'， '功能关系的应用'， '牛顿运动定律分析滑块-滑板模型问题'， '牛顿第二定律的简单应用'， '摩擦力做功']正确率40.0%如图所示，静止在水平地面上的木板质量$$M=2 k g$$，质量$$m=1 k g$$的铁块以水平初速度$${{υ}_{0}}$$从木板的左端沿板面向右滑行。已知$$\upsilon_{0}=6 m / s$$，木板与地面之间的动摩擦因数为$${{0}{.}{1}}$$，铁块与木板之间的动摩擦因数为$${{0}{.}{5}}$$，木板长为$${{4}{m}}$$，则下列说法中正确的是$${{(}{)}}$$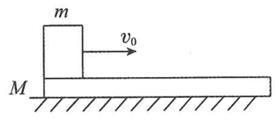
D
A.铁块最终滑离木板
B.铁块最终停在距离木板右端$${{3}{m}}$$处
C.运动过程中地面与木板之间因摩擦而产生的热量为$${{1}{8}{J}}$$
D.运动过程中铁块与木板之间因摩擦而产生的热量为$${{1}{5}{J}}$$
1. 解析：
选项分析：
A. 错误。静摩擦力和滑动摩擦力都可以做正功、负功或不做功，取决于具体情境。例如，静摩擦力在传送带上可以推动物体做正功。
B. 正确。静摩擦力和滑动摩擦力都可能不做功，例如物体在粗糙地面上静止时摩擦力不做功。
C. 错误。作用力与反作用力的功大小不一定相等，因为功还取决于位移方向。
D. 错误。作用力做正功时，反作用力可能做负功（如摩擦力）或不做功。
正确答案：B。
2. 解析：
题目描述不完整，无法直接解析。需补充斜面运动的具体条件（如高度、角度等）才能比较速度关系。
3. 解析：
选项分析：
A. 错误。同第1题，摩擦力做功情况取决于具体运动方向。
B. 正确。摩擦力可能不做功（如静止或垂直力方向运动时）。
C. 错误。静摩擦力可以不做功（如物体静止）。
D. 错误。滑动摩擦力可能不做功（如纯滚动时）。
正确答案：B。
4. 解析：
步骤分析：
1. 能量守恒：初始重力势能 $$mgh$$ 转化为克服摩擦力做功。斜面高度 $$h = AB \sin 53^\circ = 4 \, \text{m}$$，总水平位移 $$CD = 9 \, \text{m}$$。
2. 动摩擦因数计算：$$mgh = \mu mg \cos 53^\circ \cdot AB + \mu mg \cos 37^\circ \cdot BC + \mu mg \cdot CD$$，代入数据解得 $$\mu = 0.5$$。
3. 加速度比较：$$a_1 = g \sin 53^\circ - \mu g \cos 53^\circ = 5 \, \text{m/s}^2$$，$$a_2 = g \sin 37^\circ - \mu g \cos 37^\circ = 2 \, \text{m/s}^2$$，比值 $$\frac{a_1}{a_2} = \frac{5}{2}$$（选项B错误）。
4. 时间分析：因 $$AB$$ 段加速度更大，时间更短（选项C正确）。
5. 摩擦力做功：$$W_{AB} = \mu mg \cos 53^\circ \cdot AB = 15 \, \text{J}$$，$$W_{BC} = \mu mg \cos 37^\circ \cdot BC = 20 \, \text{J}$$（选项D正确）。
正确答案：ACD。
5. 解析：
题目描述不完整，需补充斜面的摩擦系数或运动条件才能判断动能、重力做功及机械能损失。
6. 解析：
步骤分析：
1. 动摩擦因数：由图乙，撤去外力后加速度 $$a = \frac{2}{5} = 0.4 \, \text{m/s}^2$$，由 $$a = \mu g$$ 得 $$\mu = 0.04$$（选项A错误）。
2. $$0 \sim 2 \, \text{s}$$ 内 $$F$$ 做功：$$F$$ 方向与位移相反，$$W = -F \cdot \Delta x$$，需结合 $$v-t$$ 图面积计算位移。
3. 摩擦生热：总位移 $$29 \, \text{m}$$，热量 $$Q = \mu mg \cdot 29 = 5.8 \, \text{J}$$（选项C错误）。
4. 总位移：$$v-t$$ 图面积计算为 $$29 \, \text{m}$$（选项D正确）。
不正确答案：AC。
7. 解析：
摩擦力分析：
1. 练习者脚与滑板间的静摩擦力 $$f_1$$ 方向向右（推动滑板），做正功。
2. 滑板与地面间的滑动摩擦力 $$f_2$$ 方向向左，做负功。
正确答案：A。
8. 解析：
能量损失分析：
1. 第一次运动损失机械能 $$\Delta E = \frac{1}{2}mgH$$，由摩擦力做功导致。
2. 第二次下落高度更低，摩擦力做功减少，能冲出 $$a$$ 点且 $$h > \frac{H}{2}$$。
正确答案：C。
9. 解析：
比较两次运动：
1. 若第二次棋子初速度更大，说明摩擦力做功更多（选项C正确）。
2. 落地速度夹角与初速度相关，初速度大则夹角小（选项B错误）。
3. 动能增量由重力做功决定，两次相同（选项D错误）。
正确答案：C。
10. 解析：
动力学分析：
1. 铁块加速度 $$a_1 = \mu_2 g = 5 \, \text{m/s}^2$$，木板加速度 $$a_2 = \frac{\mu_1 (m+M)g - \mu_2 mg}{M} = 0.5 \, \text{m/s}^2$$。
2. 相对位移：$$v_0 t - \frac{1}{2}(a_1 + a_2) t^2 = 4 \, \text{m}$$，解得 $$t = 1 \, \text{s}$$，铁块滑离木板（选项A正确）。
3. 地面摩擦生热：$$Q = \mu_1 (m+M)g \cdot x_{\text{木板}} = 3 \, \text{J}$$（选项C错误）。
4. 铁块与木板摩擦生热：$$Q = \mu_2 mg \cdot 4 = 20 \, \text{J}$$（选项D错误）。
正确答案：A。