.jpg)
正确率40.0%如图所示，木块质量为$${{M}{，}}$$放在光滑水平面上，一颗质量为$${{m}}$$的子弹以初速度$${{v}_{0}}$$水平射入木块中，射入深度为$${{d}{，}}$$平均阻力为$${{F}_{f}}$$.设木块离原点$${{s}}$$时开始匀速前进，最终速度为$${{v}{，}}$$则下列判断正确的是（）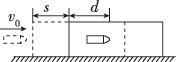
D
A.$$F_{\mathrm{f}} d=m v_{0}^{2}-m v^{2}$$
B.$$F_{\mathrm{f}} \， s=m v_{0}^{2}-( M+m ) v^{2}$$
C.$$F_{\mathrm{f}} ( s+d )=m v_{0}^{2}-( M+m ) v^{2}$$
D.上面公式均不正确
2、['牛顿第二定律'， '功能关系的应用'， '弹性势能']正确率40.0%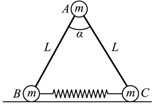
如图所示，三个小球$${{A}}$$、$${{B}}$$、$${{C}}$$的质量均为$${{m}}$$，$${{A}}$$与$${{B}}$$、$${{C}}$$间通过铰链用轻杆连接，杆长为$${{L}}$$，$${{B}}$$、$${{C}}$$置于水平地面上，用一轻质弹簧连接，弹簧处于原长。现$${{A}}$$由静止释放下降到最低点，两轻杆间夹角$${{α}}$$由$${{6}{0}{°}}$$变为$${{1}{2}{0}{°}}$$，$${{A}}$$、$${{B}}$$、$${{C}}$$在同一竖直平面内运动，弹簧在弹性限度内，忽略一切摩擦，重力加速度为$${{g}}$$。则此下降过程中$${{(}{)}}$$
A.释放$${{A}}$$的瞬间，$${{B}}$$受到地面的支持力等于$$1. 5 m g$$
B.$${{A}}$$的动能最大时，$${{B}}$$受到地面的支持力等于$$1. 5 m g$$
C.弹簧的弹性势能最大时，$${{A}}$$的加速度等于$${{0}}$$
D.弹簧的弹性势能最大值和系统动能的最大值相同
3、['功能关系的应用'， '功率'， '电功与电功率定义、表达式、物理意义及简单应用'， '能量守恒定律']正确率80.0%我国高铁的发展大幅提高铁路客货运输能力，有关资料表明，高铁以时速$$3 5 0 k m$$运行时每小时耗电$${{9}{6}{0}{0}}$$度、以时速$$2 5 0 k m$$运行时每小时耗电$${{4}{8}{0}{0}}$$度。高铁消耗的电能主要供给高铁的动力牵引系统，若不计其它系统、其它原因的电能消耗，则高铁在时速$$3 5 0 k m$$、$$2 5 0 k m$$时的阻力之比为$${{(}{)}}$$
A.$${{2}}$$：$${{1}}$$
B.$${{1}{0}}$$：$${{7}}$$
C.$${{7}}$$：$${{5}}$$
D.$${{1}{4}}$$：$${{5}}$$
4、['万有引力定律的常见应用'， '功能关系的应用'， '人造卫星的运行规律']正确率80.0%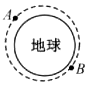
我国第一颗人造地球卫星东方红一号已经运行了$${{5}{0}}$$多年$${{.}}$$如图所示，$${{A}}$$、$${{B}}$$是东方红一号绕地球运动的远地点和近地点，则东方红一号$${{(}{)}}$$
B
A.在$${{A}}$$点的角速度大于$${{B}}$$点的角速度
B.在$${{A}}$$点的加速度小于$${{B}}$$点的加速度
C.由$${{A}}$$运动到$${{B}}$$过程中动能减小，势能增加
D.由$${{A}}$$运动到$${{B}}$$过程中引力做正功，机械能增大
5、['用牛顿运动定律分析斜面体模型'， '简谐运动的定义及特征'， '用牛顿运动定律分析弹簧类问题'， '受力分析'， '功能关系的应用'， '利用机械能守恒解决简单问题'， '动能定理的简单应用']正确率19.999999999999996%如图所示，一轻弹簧下端固定在倾角为$${{θ}}$$的光滑斜面底端，弹簧处于原长时上端在$${{O}}$$点，将一质量为$${{M}}$$的物块甲轻放在弹簧上端，物块甲下滑到$${{A}}$$点时速度最大，下滑到最低点$${{B}}$$时加速度大小为$$g \operatorname{s i n} \theta， \， \， \， O， \， \， \， B$$间距为$${{L}}$$。换用另一质量为$${{m}}$$的物块乙，从距$${{O}}$$点为$${{L}}$$的$${{C}}$$点静止释放，也刚好将弹簧压缩到$${{B}}$$点，不计空气阻力，弹簧始终在弹性限度内，重力加速度大小为$${{g}}$$，则$${{(}{)}}$$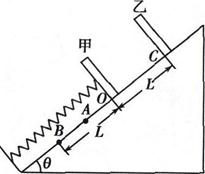
C
A.甲$${、}$$乙的质量之比为$${{1}{︰}{4}}$$
B.乙运动到$${{O}}$$点下方$$\frac{L} {2}$$处时速度最大
C.乙的最大速度为$${\frac{3} {2}} \sqrt{g L \operatorname{s i n} \theta}$$
D.乙在$${{B}}$$点时加速度大小为$${{2}{g}{{s}{i}{n}}{θ}}$$
6、['万有引力定律的简单计算'， '功能关系的应用'， '动能和势能的转化']正确率60.0%由于地球对周围物体的吸引，而使物体具有的引力势能可表示为$$E_{p}=-\frac{G M m} {r} \langle$$选无限远引力势能为$${{0}{）}}$$，其中$${{G}}$$为引力常量$${、{M}}$$为地球质量$${、{m}}$$为物体质量$${、{r}}$$为物体到地心的距离。现利用火箭将质量为$${{m}_{0}}$$的人造地球卫星从地面发射到距地心为$${{R}_{1}}$$的回形轨道上做匀速圆周运动。已知地球质量为$${{M}{、}}$$地球半径为$${{R}}$$，忽略地球自转及空气阻力作用，则在此过程中，火箭至少做功为（）
C
A.$$\frac{G M m_{1}} {2 R_{1}}$$
B.$$- \frac{G M m_{1}} {2 R_{1}}$$
C.$$G M m_{0} \ ( \frac{1} {R}-\frac{1} {2 R_{1}} )$$
D.$$G M m_{0} \ ( \frac{1} {R_{1}}-\frac{1} {R} )$$
7、['动量定理的内容及表达式'， '冲量的定义、单位和矢量性'， '动量守恒-系统受到外力矢量和为0'， '功能关系的应用'， '判断系统机械能是否守恒']正确率40.0%如图所示，一个小滑块从静止在地面上的斜面上由静止滑下，所有接触面都是光滑的。则下列说法中正确的是$${{(}{)}}$$
B
A.由于没有任何摩擦损失，所以小滑块的机械能是不变的
B.小滑块在下滑的过程中，其机械能一直是减少的
C.小滑块由顶端滑到底端的过程中，其动量变化量与重力的冲量是相同的
D.小滑块由顶端滑到底端的过程中，小滑块与斜面组成的系统总动量守恒
8、['用牛顿运动定律分析弹簧类问题'， '功能关系的应用'， '从受力确定运动情况']正确率40.0%
如图，一轻质弹簧放在光滑斜面上且下端固定，一质量为$${{m}}$$
C
A.由$${{B}}$$到$${{C}}$$，滑块一直做减速运动
B.由$${{A}}$$到$${{C}}$$，滑块的机械能守恒
C.由$${{B}}$$到$${{C}}$$，弹性势能和滑块动能之和逐渐增大
D.在$${{C}}$$处，滑块的合外力为零
9、['功能关系的应用'， '卫星变轨问题'， '判断某个力是否做功，做何种功'， '开普勒行星运动定律']正确率40.0%$${{2}{0}{1}{6}}$$年$${{1}{0}}$$月$${{1}{7}}$$日，景海鹏和陈冬搭乘$${{“}}$$神舟十一号$${{”}}$$飞船飞向太空，于$${{1}{1}}$$月$${{1}{8}}$$日乘返回舱安全返回。返回舱在 $${{A}}$$点从圆形轨道$${Ⅰ}$$进入椭圆轨道$${Ⅱ}$$，如图所示。关于返回舱的运动，下列说法中正确的有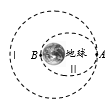
D
A.飞船在轨道$${Ⅰ}$$上经过 $${{A}}$$时需向运动的反方向喷气才能进入椭圆轨道$${Ⅱ}$$
B.飞船变轨后机械能不变
C.飞船在轨道$${Ⅱ}$$上运动的周期大于在轨道$${Ⅰ}$$上运动的周期
D.飞船在轨道$${Ⅱ}$$上由 $${{A}}$$向 $${{B}}$$运动的过程中地球对飞船的引力做正功
10、['环绕天体运动参量的分析与计算'， '万有引力定律的其他应用'， '功能关系的应用'， '向心力'， '卫星变轨问题']正确率40.0%科幻电影$${《}$$流浪地球$${》}$$讲述了太阳即将毁灭，人类无法生存，开启了$${{“}}$$流浪地球$${{”}}$$计划，试图带着地球一起逃离太阳系，寻找新家园．如图所示，若地球最初沿轨道$${Ⅲ}$$绕太阳做匀速圆周运动，通过多次的变轨最终逃离太阳系．下列说法正确的是（）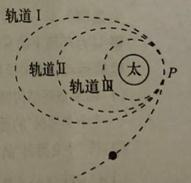
C
A.地球在轨道$${Ⅲ}$$上经过$${{P}}$$点时的运行速度和在轨道$${Ⅱ}$$上经过$${{P}}$$点时的运行速度相等
B.地球在轨道$${Ⅲ}$$上经过$${{P}}$$点时的加速度比在轨道$${Ⅰ}$$上经过$${{P}}$$点时的加速度小
C.地球在轨道$${Ⅰ}$$上的机械能比在轨道$${Ⅱ}$$上的机械能大
D.地球在轨道$${Ⅰ}$$上的机械能比在轨道$${Ⅲ}$$上的机械能小
1. 解析：根据动量守恒和能量守恒分析子弹和木块系统。
子弹射入木块过程中，动量守恒：$$m v_0 = (M + m) v$$。
阻力做功等于系统动能损失：$$F_f d = \frac{1}{2} m v_0^2 - \frac{1}{2} (M + m) v^2$$。
木块从开始运动到匀速时，阻力做功为：$$F_f s = \frac{1}{2} M v^2$$。
综合以上两式得：$$F_f (s + d) = \frac{1}{2} m v_0^2 - \frac{1}{2} (M + m) v^2$$，即选项C正确。
2. 解析：分析A下降过程中受力及能量变化。
A释放瞬间，系统受力平衡：$$3mg = N_B + N_C$$，由于对称性，$$N_B = N_C = 1.5mg$$，选项A正确。
A动能最大时，加速度为零，受力平衡，支持力仍为$$1.5mg$$，选项B正确。
弹簧弹性势能最大时，A速度为零，但加速度不为零（向上），选项C错误。
系统动能最大值等于重力势能减少量减去弹性势能，两者不相等，选项D错误。
3. 解析：高铁阻力与速度关系为$$F \propto v^2$$，功率$$P = Fv \propto v^3$$。
耗电功率比为$$9600:4800 = 2:1$$，速度比为$$350:250 = 7:5$$。
由$$P \propto v^3$$得阻力比为$$\frac{2}{7^3} : \frac{1}{5^3} = 250:343 \approx 10:7$$，选项B正确。
4. 解析：卫星运动遵循开普勒定律。
A点距离地心较远，角速度较小，选项A错误。
由$$a = \frac{GM}{r^2}$$知，A点加速度较小，选项B正确。
由A到B过程中引力做正功，动能增大，势能减小，机械能守恒，选项C、D错误。
5. 解析：分析弹簧压缩过程能量关系。
甲在B点加速度为$$g \sin \theta$$，说明弹簧弹力为$$Mg \sin \theta$$。
乙从C到B过程中，能量守恒：$$mg \cdot 2L \sin \theta = \frac{1}{2} k L^2$$。
甲从O到B过程中：$$Mg L \sin \theta = \frac{1}{2} k L^2$$。
联立得$$m = 4M$$，即质量比为1:4，选项A正确。
乙速度最大时受力平衡，弹簧压缩量为$$\frac{L}{2}$$，选项B正确。
乙最大速度为$$\sqrt{2gL \sin \theta}$$，选项C错误。
乙在B点加速度为$$2g \sin \theta$$，选项D正确。
6. 解析：火箭做功等于卫星机械能增量。
卫星在轨道上的机械能为$$E = -\frac{GMm_0}{2R_1}$$。
地面引力势能为$$E_p = -\frac{GMm_0}{R}$$。
火箭做功为$$W = \frac{GMm_0}{R} - \frac{GMm_0}{2R_1}$$，选项C正确。
7. 解析：分析小滑块下滑过程。
斜面会移动，小滑块机械能不守恒，选项A错误。
斜面支持力对小滑块做负功，机械能减少，选项B正确。
动量变化量等于合外力冲量（重力冲量加支持力冲量），选项C错误。
系统水平方向动量守恒，总动量不守恒，选项D错误。
8. 解析：滑块运动过程分析。
由B到C，滑块先加速后减速，选项A错误。
机械能不守恒（弹簧弹力做功），选项B错误。
弹性势能和动能之和等于重力势能减少量，逐渐增大，选项C正确。
C处滑块加速度不为零，选项D错误。
9. 解析：飞船变轨过程分析。
飞船需减速进入椭圆轨道，选项A错误。
变轨后机械能减少，选项B错误。
轨道Ⅱ半长轴小于轨道Ⅰ半径，周期更小，选项C错误。
A到B过程中引力做正功，选项D正确。
10. 解析：地球变轨过程分析。
轨道Ⅲ到Ⅱ需加速，速度不等，选项A错误。
P点加速度由万有引力决定，与轨道无关，选项B错误。
轨道Ⅰ半径最大，机械能最大，选项C正确、D错误。