.jpg)
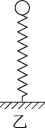
正确率40.0%如图甲所示，一竖直悬挂的轻质弹簧上端固定、下端连接质量为$${{m}}$$的小球，弹簧的劲度系数为$${{k}{，}}$$小球静止时弹簧长度为$${{L}}$$.将整个装置倒置过来如图乙所示，将弹簧竖直向上拉至长为$${{L}{，}}$$由静止释放并开始计时，小球做简谐运动的周期为$${{T}}$$.以平衡位置为坐标原点，取竖直向下为正方向，重力加速度为$${{g}{，}}$$空气阻力不计，弹簧始终在弹性限度内，则小球运动的位移$${{x}}$$随时间$${{t}}$$的表达式为（）
D
A.$$x=\frac{m g} {k} \cdot\operatorname{s i n} \left( \frac{2 \pi} {T} t+\frac{\pi} {2} \right)$$
B.$$x=\frac{2 m g} {k} \cdot\operatorname{s i n} \left( \frac{2 \pi} {T} t+\frac{\pi} {2} \right)$$
C.$$x=\frac{m g} {k} \cdot\operatorname{s i n} \left( \frac{2 \pi} {T} t-\frac{\pi} {2} \right)$$
D.$$x=\frac{2 m g} {k} \cdot\operatorname{s i n} \left( \frac{2 \pi} {T} t-\frac{\pi} {2} \right)$$
2、['对简谐运动的表达式的理解'， '描述简谐运动的物理量'， '简谐运动振动图象'， '振动图像'， '波动图像']正确率0.0%一列简谐横波在$${{t}{=}{{1}{.}{0}}{s}}$$时的波形图如图甲所示$${，{P}}$$是介质中的质点，图乙是质点$${{P}}$$的振动图像，已知该波在介质中的传播速度为$${{1}{0}{{m}{/}{s}}{，}}$$则（）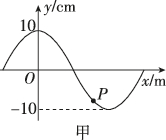
D
A.该波沿$${{x}}$$轴负方向传播
B.再经过$$0. 6 \mathrm{s}，$$质点$${{P}}$$运动的路程为$${{6}{m}}$$
C.$${{t}{=}{{1}{.}{0}}{s}}$$时质点$${{P}}$$离开平衡位置的位移$${{−}{5}{\sqrt {2}}{{c}{m}}}$$
D.质点$${{P}}$$的平衡位置坐标为$${{x}{=}{5}{m}}$$
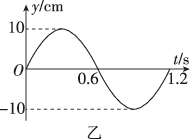
3、['对简谐运动的表达式的理解'， '振动图像'， '波动图像'， '波速、波长和频率（周期）的关系']正确率40.0%一列简谐横波沿$${{x}}$$轴正方向传播，图甲是$${{t}{=}{0}}$$时的波形图，图乙和图丙分别是$${{x}}$$轴上$${{M}{、}{N}}$$两质点的振动图象．则下列说法错误的是$${{(}{)}}$$
C
A.质点$${{M}}$$离开平衡位置位移的瞬时值表达式为$$y=0. 1 \operatorname{c o s} \pi t ( m )$$
B.质点$${{N}}$$在$${{t}{=}{0}}$$时的加速度是振动过程中最大值的$$\frac{1} {2}$$
C.质点$${{M}{、}{N}}$$平衡位置之间的距离可能为$${\frac{5} {4}} m$$
D.质点$${{M}{、}{N}}$$的速度方向有时相同有时相反
4、['对简谐运动的表达式的理解'， '振动图像与波动图像的综合应用'， '波速、波长和频率（周期）的关系']正确率40.0%一简谐横波沿$${{x}}$$轴传播，已知$${{t}{=}{0}}$$时的波形如图甲所示，质点$${{P}}$$的振动图象如图乙所示$${{(}{)}}$$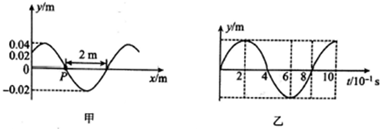
D
A.波向$${{x}}$$轴正方向传动，传播速度等于$$2. 5 m / s$$
B.$${{0}}$$时刻$${{x}{=}{0}}$$处的质点再过$${{0}{.}{1}{s}}$$到达波峰
C.$${{x}{=}{0}}$$处的质点在$${{t}{=}{4}{s}}$$时速度为$${{0}}$$
D.$${{P}}$$质点的$${{x}}$$坐标为$${\frac{5} {3}} m$$
5、['对简谐运动的表达式的理解']正确率60.0%已知弹簧振子的位移$${{x}}$$随时间$${{t}}$$变化的表达式为$$x=8 \operatorname{s i n} ~ ( 4 \pi t+{\frac{\pi} {6}} ) ~ c m$$，式中位移$${{x}}$$的单位是$${{c}{m}}$$，时间$${{t}}$$的单位是$${{s}}$$．下列说法正确的是（）
B
A.弹簧振子的振幅为$${{1}{6}{c}{m}}$$
B.弹簧振子的振动周期为$${{0}{.}{5}{s}}$$
C.在$${{t}{=}{0}}$$时，弹簧振子的速度达到最大
D.在$${{t}{=}{0}}$$时，弹簧振子离开平衡位置的位移达到最大
6、['对简谐运动的表达式的理解']正确率40.0%某质点做简谐运动，其位移随时间变化的关系式为$$x=5 \operatorname{s i n} {\frac{\pi} {4}} t ( \mathrm{c m} )$$，则下列关于质点运动的说法中正确的是（）
C
A.质点做简谐运动的振幅为$${{1}{0}{{c}{m}}}$$
B.质点做简谐运动的周期为$${{4}{s}}$$
C.在$${{t}{=}{4}{s}}$$时质点的速度最大
D.在$${{t}{=}{4}{s}}$$时质点的加速度最大
7、['对简谐运动的表达式的理解'， '描述简谐运动的物理量'， '简谐运动振动图象'， '简谐运动的回复力和能量问题'， '振动图像']正确率40.0%装有一定量液体的玻璃管竖直漂浮在水中，水面足够大，如图甲所示。把玻璃管向下缓慢按压$${{4}{c}{m}}$$后放手，忽略运动阻力，玻璃管的运动可以视为竖直方向的简谐运动，测得振动周期为$${{0}{.}{5}{s}}$$。竖直向上为正方向，某时刻开始计时，其振动图象如图乙所示，其中$${{A}}$$为振幅。对于玻璃管，下列说法正确的是$${{(}{)}}$$
C
A.玻璃管受重力$${、}$$浮力和回复力作用
B.在$${{t}_{1}{∼}{{t}_{2}}}$$时间内，加速度与速度方向相反
C.位移满足函数式$$x=4 \operatorname{s i n} ( 4 \pi t-\frac{5} {6} \pi) c m$$
D.振动频率与按压的深度有关
8、['对简谐运动的表达式的理解'， '简谐运动的回复力和能量问题']正确率80.0%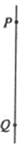
如图所示，$${{P}{Q}}$$为一竖直弹簧振子振动路径上的两点，振子经过$${{P}}$$点时的加速度大小为$${{6}{m}{/}{{s}^{2}}}$$，方向指向$${{Q}}$$点；当振子经过$${{Q}}$$点时，加速度的大小为$${{8}{m}{/}{{s}^{2}}}$$，方向指向$${{P}}$$点。若$${{P}{Q}}$$之间的距离为$${{1}{4}{c}{m}}$$，已知振子的质量为$${{1}{k}{g}}$$，则以下说法正确的是$${{(}{)}}$$
C
A.振子经过$${{P}}$$点时所受的合力比经过$${{Q}}$$点时所受的合力大
B.该弹簧振子的平衡位置在$${{P}}$$点正下方$${{7}{c}{m}}$$处
C.振子经过$${{P}}$$点时的速度比经过$${{Q}}$$点时的速度大
D.该弹簧振子的振幅一定为$${{8}{c}{m}}$$
9、['对简谐运动的表达式的理解'， '简谐运动振动图象'， '简谐运动的回复力和能量问题']正确率80.0%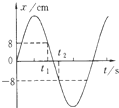
物体做简谐运动，其振动图象如图所示，在$${{t}_{1}}$$时刻和$${{t}_{2}}$$时刻，物体的$${{(}{)}}$$
C
A.回复力相同
B.位移相同
C.速度相同
D.加速度相同
10、['对简谐运动的表达式的理解'， '描述简谐运动的物理量'， '简谐运动振动图象']正确率80.0%做简谐运动的物体，其位移随时间的变化规律为$$x=2 \operatorname{s i n} ( 5 \pi t+\frac{\pi} {6} ) c m$$，则下列说法正确的是$${{(}{)}}$$
D
A.它的振幅为$${{4}{c}{m}}$$
B.它的周期为$$0. 0 2 s$$
C.它的初相位是$$\frac{\pi} {3}$$
D.它在$$\frac{1} {4}$$周期内通过的路程可能是$${{2}{\sqrt {2}}{c}{m}}$$
1. 解析：
在甲图中，弹簧悬挂小球静止时，弹簧伸长量为$$x_1 = \frac{mg}{k}$$，弹簧长度为$$L = L_0 + x_1$$，其中$$L_0$$为弹簧原长。
在乙图中，弹簧被拉至长度$$L$$，此时弹簧伸长量为$$x_2 = L - L_0 = x_1$$。释放后，小球做简谐运动，振幅$$A = x_1 = \frac{mg}{k}$$。
简谐运动的位移表达式为$$x = A \sin\left(\frac{2\pi}{T}t + \phi\right)$$。初始时刻$$t=0$$时，弹簧处于最大伸长位置，位移为$$-A$$，因此初相位$$\phi = -\frac{\pi}{2}$$。
综上，位移表达式为$$x = \frac{mg}{k} \sin\left(\frac{2\pi}{T}t - \frac{\pi}{2}\right)$$，选项C正确。
2. 解析：
由乙图可知，$$t=1.0\,s$$时质点$$P$$向上振动，结合甲图波形，波沿$$x$$轴负方向传播，选项A正确。
波的周期$$T = \frac{\lambda}{v} = \frac{10\,m}{10\,m/s} = 1\,s$$。再经过$$0.6\,s$$（$$0.6T$$），质点$$P$$运动的路程为$$6A = 6 \times 10\,cm = 0.6\,m$$，选项B错误。
$$t=1.0\,s$$时，质点$$P$$在平衡位置上方，位移为$$-5\sqrt{2}\,cm$$，选项C正确。
由甲图可知，$$P$$的平衡位置坐标为$$x=5\,m$$，选项D正确。
3. 解析：
由乙图可知，质点$$M$$的振动方程为$$y = 0.1 \cos(\pi t)\,m$$，选项A正确。
质点$$N$$在$$t=0$$时的位移为$$y = 0.05\,m$$，加速度$$a = -\omega^2 y$$，最大加速度为$$\omega^2 A$$，因此此时加速度为最大值的一半，选项B正确。
由甲图和乙图可知，$$M$$和$$N$$的相位差为$$\frac{\pi}{2}$$，距离可能为$$\frac{\lambda}{4} = \frac{5}{4}\,m$$，选项C正确。
$$M$$和$$N$$的速度方向可能相同或相反，选项D正确。题目要求选择错误的说法，因此无错误选项。
4. 解析：
由乙图可知，$$t=0$$时质点$$P$$向下振动，结合甲图波形，波沿$$x$$轴正方向传播，波速$$v = \frac{\lambda}{T} = \frac{10\,m}{4\,s} = 2.5\,m/s$$，选项A正确。
$$x=0$$处的质点在$$t=0$$时位于平衡位置且向下振动，再过$$0.1\,s$$（$$T/4$$）到达波谷，选项B错误。
$$x=0$$处的质点在$$t=4\,s$$时回到平衡位置，速度最大，选项C错误。
由甲图和乙图可知，$$P$$的$$x$$坐标为$$\frac{5}{3}\,m$$，选项D正确。
5. 解析：
由表达式$$x = 8 \sin(4\pi t + \frac{\pi}{6})\,cm$$可知，振幅为$$8\,cm$$，选项A错误。
周期$$T = \frac{2\pi}{\omega} = \frac{2\pi}{4\pi} = 0.5\,s$$，选项B正确。
$$t=0$$时，位移$$x = 8 \sin\left(\frac{\pi}{6}\right) = 4\,cm$$，未达到最大位移，速度不为零，选项C和D错误。
6. 解析：
由表达式$$x = 5 \sin\left(\frac{\pi}{4} t\right)\,cm$$可知，振幅为$$5\,cm$$，选项A错误。
周期$$T = \frac{2\pi}{\omega} = \frac{2\pi}{\pi/4} = 8\,s$$，选项B错误。
$$t=4\,s$$时，质点经过平衡位置，速度最大，选项C正确。
$$t=4\,s$$时，加速度为零，选项D错误。
7. 解析：
玻璃管受重力和浮力作用，回复力是两者的合力，选项A错误。
在$$t_1 \sim t_2$$时间内，玻璃管向平衡位置运动，加速度与速度方向相同，选项B错误。
由振动图像可知，振幅$$A=4\,cm$$，初相位为$$-\frac{5}{6}\pi$$，位移表达式为$$x = 4 \sin\left(4\pi t - \frac{5}{6}\pi\right)\,cm$$，选项C正确。
振动频率与系统本身性质有关，与按压深度无关，选项D错误。
8. 解析：
振子在$$P$$点和$$Q$$点的加速度分别为$$6\,m/s^2$$和$$8\,m/s^2$$，合力$$F = ma$$，因此$$Q$$点合力更大，选项A错误。
设平衡位置为$$O$$，$$OP = x$$，$$OQ = 14 - x$$。由简谐运动性质有$$a_P = \omega^2 x = 6$$，$$a_Q = \omega^2 (14 - x) = 8$$，解得$$x = 6\,cm$$，平衡位置在$$P$$点下方$$6\,cm$$处，选项B错误。
振子经过平衡位置时速度最大，因此经过$$P$$点时的速度比$$Q$$点小，选项C错误。
振幅$$A = x + 2 = 8\,cm$$，选项D正确。
9. 解析：
$$t_1$$和$$t_2$$时刻，物体的位移大小相等、方向相反，回复力和加速度方向相反，选项A、B、D错误。
速度方向相同，选项C正确。
10. 解析：
由表达式$$x = 2 \sin\left(5\pi t + \frac{\pi}{6}\right)\,cm$$可知，振幅为$$2\,cm$$，选项A错误。
周期$$T = \frac{2\pi}{5\pi} = 0.4\,s$$，选项B错误。
初相位为$$\frac{\pi}{6}$$，选项C错误。
$$\frac{1}{4}$$周期内路程可能为$$2\sqrt{2}\,cm$$，选项D正确。