.jpg)
正确率40.0%如图所示小球$${{A}}$$挂在轻质弹簧下端在上下振动，小球$${{B}}$$在竖直平面内以$${{O}}$$为圆心做匀速圆周运动，用水平平行光照射小球$${{B}{，}}$$可以观察到小球$${{B}}$$的投影总和小球$${{A}}$$重合，已知小球$${{A}}$$的质量为$${{m}{，}}$$小球$${{B}}$$做圆周运动半径为$${{R}{，}}$$角速度$${{ω}{=}}$$$$\sqrt{\frac{g} {R}} ( g$$为重力加速度)， 弹簧振子周期$$T=2 \pi\sqrt{\frac{m} {k}} ( k$$为弹簧的劲度系数)， 下列说法正确的是（）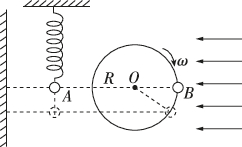
D
A.弹簧的劲度系数$$k=\frac{m g} {2 R}$$
B.小球$${{A}}$$和小球$${{B}}$$的运动周期不相等
C.小球$${{A}}$$在最低点的回复力大小为$${{2}{m}{g}}$$
D.小球$${{A}}$$做简谐运动的加速度最大值为$${{g}}$$
2、['简谐运动的定义及特征'， '简谐运动的回复力和能量问题'， '弹簧振子运动过程各物理量变化规律']正确率60.0%弹簧振子做简谐运动时，以下说法不正确的是（）
D
A.振子通过平衡位置时，回复力一定为零
B.振子做减速运动时，加速度却在增大
C.振子远离平衡位置运动时，加速度方向与速度方向相反
D.振子向平衡位置运动时，加速度方向与速度方向相反
3、['对简谐运动的表达式的理解'， '弹簧振子运动过程各物理量变化规律']正确率60.0%一弹簧振子的位移$${{y}}$$随时间$${{t}}$$变化的关系式为$$y=0. 1 \operatorname{s i n} 2. 5 \pi t$$，位移$${{y}}$$的单位为$${{m}}$$，时间$${{t}}$$的单位为$${{s}}$$.则$${{(}{)}}$$
D
A.弹簧振子的振幅为$${{0}{.}{2}{m}}$$
B.弹簧振子的周期为$$1. 2 5 \; s$$
C.在$${{t}{=}{{0}{.}{2}}{s}}$$时，振子的位移为零
D.在$${{t}{=}{{0}{.}{2}}{s}}$$时，振子的振动速度为零
4、['描述简谐运动的物理量'， '弹簧振子运动过程各物理量变化规律']正确率60.0%一简谐横波沿水平绳向右传播，波速为$${{v}}$$，周期为$${{T}}$$，振幅为$${{A}}$$。绳上两质点$${{M}{、}{N}}$$的平衡位置相距$${{3}{/}{4}}$$波长，$${{N}}$$位于$${{M}}$$右方。设向上为正，在$${{t}{=}{0}}$$时$${{M}}$$位移为$${{+}{A}{/}{2}}$$，且向上运动；经时间$$t ( t < T )， \， \， M$$位移仍为$${{+}{A}{/}{2}}$$，但向下运动，则$${{(}{)}}$$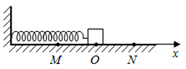
C
A.在$${{t}}$$时刻，$${{N}}$$恰好在波谷位置
B.在$${{t}}$$时刻，$${{N}}$$位移为负，速度向上
C.在$${{t}}$$时刻，$${{N}}$$位移为负，速度向下
D.在$${{2}{t}}$$时刻，$${{N}}$$位移为$${{−}{A}{/}{2}}$$，速度向下
5、['弹簧振子运动过程各物理量变化规律']正确率60.0%如图是光滑水平面上的一个弹簧振子。把振子由平衡位置拉到位置$${{B}}$$，再放开，它就沿着水平面在$${{B}{、}{C}}$$之间振动，振动周期是$${{0}{.}{4}{s}}$$。若在振子由$${{C}}$$向$${{B}}$$运动至$${{O}}$$点时刻开始计时，则$${{t}{=}{{0}{.}{1}{5}}{s}}$$时$${{(}{)}}$$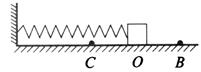
C
A.振子正在从$${{C}}$$向$${{O}}$$运动
B.振子正在从$${{O}}$$向$${{B}}$$运动
C.振子正在从$${{B}}$$向$${{O}}$$运动
D.振子正在从$${{O}}$$向$${{C}}$$运动
6、['弹簧振子运动过程各物理量变化规律']正确率60.0%做简谐运动的弹簧振子质量为$$0. 2 k g$$，当它运动到平衡位置左侧$${{2}{0}{c}{m}}$$时，受到的回复力是$${{4}{N}}$$；当它运动到平衡位置右侧$${{4}{0}{c}{m}}$$时，它的加速度为（）
D
A.$$2 0 m / s^{2}$$，向右
B.$$2 0 m / s^{2}$$，向左
C.$$4 0 m / s^{2}$$，向右
D.$$4 0 m / s^{2}$$，向左
7、['弹簧振子运动过程各物理量变化规律']正确率60.0%一个弹簧振子做简谐运动，当它向平衡位置运动的过程中，下列关于它运动速度$${、}$$加速度变化的说法中，正确的是$${{(}{)}}$$
A
A.速度增大，加速度减小
B.速度减小，加速度增大
C.速度增大，加速度增大
D.速度减小，加速度减小
8、['弹簧振子运动过程各物理量变化规律']正确率40.0%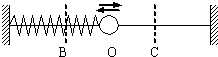
如图所示，$${{O}}$$
C
A.速度不断增大，加速度不断增大
B.速度不断减小，加速度不断增大
C.速度不断增大，加速度不断减小
D.速度不断减小，加速度不断减小
9、['弹簧振子运动过程各物理量变化规律']正确率60.0%如图所示，$${{O}}$$为弹簧振子平衡位置，将振子拉至$${{A}}$$处后放手，振子可沿水平光滑杆在$${{A}{、}{B}}$$间作简谐振动，则振子$${{(}{)}}$$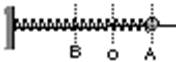
B
A.从$${{B}{→}{O}}$$回复力不断减小，速度不断减小
B.在$${{O}}$$处速度最大
C.从$${{B}{→}{O}}$$回复力不断增大，速度不断增大
D.在$${{B}}$$处速度最大
10、['描述简谐运动的物理量'， '弹簧振子运动过程各物理量变化规律']正确率60.0%一弹簧振子沿水平方向的$${{x}}$$轴做简谐运动，原点$${{O}}$$为平衡位置，在运动中某一时刻有可能出现的情况是（）
A
A.位移与速度均为正值，加速度为负值
B.位移$${、}$$速度与加速度均为正值
C.位移与加速度均为正值，而速度为负值
D.位移$${、}$$速度$${、}$$加速度均为负值
1. 解析：
小球$$B$$的投影与小球$$A$$重合，说明两者运动同步，周期相同。小球$$B$$的周期$$T_B = \frac{2\pi}{\omega} = 2\pi\sqrt{\frac{R}{g}}$$，而弹簧振子的周期$$T_A = 2\pi\sqrt{\frac{m}{k}}$$，由$$T_A = T_B$$可得$$k = \frac{mg}{R}$$，选项A错误。
小球$$A$$在最低点的回复力$$F = kx$$，振幅$$x = R$$，故$$F = \frac{mg}{R} \cdot R = mg$$，选项C错误。
简谐运动的加速度最大值$$a_{\text{max}} = \omega^2 A = \frac{g}{R} \cdot R = g$$，选项D正确。
小球$$A$$和小球$$B$$的周期相等，选项B错误。
答案：D
2. 解析：
振子向平衡位置运动时，加速度方向与速度方向相同，选项D错误。
答案：D
3. 解析：
由$$y = 0.1\sin(2.5\pi t)$$可知振幅$$A = 0.1\,m$$，选项A错误。
周期$$T = \frac{2\pi}{\omega} = \frac{2\pi}{2.5\pi} = 0.8\,s$$，选项B错误。
$$t = 0.2\,s$$时，$$y = 0.1\sin(0.5\pi) = 0.1\,m$$，位移不为零，选项C错误。
此时振子位于最大位移处，速度为零，选项D正确。
答案：D
4. 解析：
$$M$$和$$N$$相距$$\frac{3}{4}\lambda$$，$$N$$的振动比$$M$$滞后$$\frac{3}{4}T$$。在$$t = 0$$时，$$M$$向上运动，位移为$$+\frac{A}{2}$$；经时间$$t$$，$$M$$位移仍为$$+\frac{A}{2}$$但向下运动，说明$$t = \frac{T}{6}$$。
此时$$N$$的相位滞后$$\frac{3}{4}T$$，其位移为负且速度向下，选项C正确。
答案：C
5. 解析：
周期$$T = 0.4\,s$$，$$t = 0.15\,s$$为$$\frac{3}{8}T$$，振子正从$$B$$向$$O$$运动，选项C正确。
答案：C
6. 解析：
回复力$$F = -kx$$，由$$4 = -k \cdot (-0.2)$$得$$k = 20\,N/m$$。在右侧$$x = 0.4\,m$$时，加速度$$a = -\frac{k}{m}x = -\frac{20}{0.2} \cdot 0.4 = -40\,m/s^2$$，方向向左。
答案：D
7. 解析：
振子向平衡位置运动时，速度增大，加速度减小，选项A正确。
答案：A
8. 解析：
题目不完整，无法解析。
9. 解析：
从$$B \to O$$，回复力减小，速度增大，选项A、C错误。在$$O$$处速度最大，选项B正确。
答案：B
10. 解析：
位移为正值时，加速度为负值；速度方向由运动方向决定，可能为正或负。选项A可能出现。
答案：A