.jpg)
正确率60.0%有一个在光滑水平面内的弹簧振子，第一次用力把弹簧压缩$${{x}}$$长度后释放让它振动，第二次把弹簧压缩$${{2}{x}}$$长度后释放让它振动，则先后两次振动的周期之比和振幅之比分别为（）
B
A.$${{1}}$$∶$${{1}}$$、$${{1}}$$∶$${{1}}$$
B.$${{1}}$$∶$${{1}}$$、$${{1}}$$∶$${{2}}$$
C.$${{1}}$$∶$${{4}}$$、$${{1}}$$∶$${{4}}$$
D.$${{1}}$$∶$${{2}}$$、$${{1}}$$∶$${{2}}$$
2、['弹簧振子运动过程各物理量变化规律']正确率40.0%如图所示，做简谐运动的水平弹簧振子从平衡位置$${{O}}$$向$${{B}}$$运动的过程中，下述正确的是$${{(}{)}}$$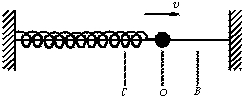
D
A.振子做匀减速运动
B.振子做匀加速运动
C.振子做加速度不断减小的减速运动
D.振子做加速度不断增大的减速运动
3、['简谐运动的回复力和能量问题'， '弹簧振子运动过程各物理量变化规律']正确率40.0%弹簧振子在光滑水平面上做简谐运动，在振子向平衡位置运动的过程中（）
C
A.弹簧振子相对平衡位置的位移逐渐增大
B.弹簧振子的加速度逐渐增大
C.弹簧振子的速度逐渐增大
D.弹簧振子的势能逐渐增大
4、['弹簧振子的位移时间图像'， '弹簧振子运动过程各物理量变化规律']正确率60.0%如图为某一弹簧振子做简谐振动的图象，在$${{t}_{1}}$$到$${{t}_{2}}$$时间内下列物理量变小的是（）
B
A.位移
B.速度
C.回复力
D.振幅
5、['弹簧振子运动过程各物理量变化规律']正确率80.0%如图所示，$${{O}}$$是弹簧振子的平衡位置，小球在$${{B}{、}{C}}$$之间做无摩擦的往复运动，则小球任意两次经过$${{O}}$$点可能不同的物理量是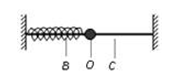
D
A.加速度
B.机械能
C.回复力
D.速度
6、['弹簧振子的回复力和能量'， '弹簧振子运动过程各物理量变化规律']正确率40.0%如图所示，在光滑水平面上有一质量为$${{m}}$$的小物块与左端固定的轻质弹簧相连，构成一个水平弹簧振子，弹簧处于原长时小物块位于$${{O}}$$点.现使小物块在$${{M}}$$、$${{N}}$$两点间沿光滑水平面做简谐运动，在此过程中（）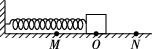
B
A.小物块运动到$${{M}}$$点时回复力与位移方向相同
B.小物块每次运动到$${{N}}$$点时的加速度一定相同
C.小物块从$${{O}}$$点向$${{M}}$$点运动过程中做加速运动
D.小物块从$${{O}}$$点向$${{N}}$$点运动过程中机械能增加
7、['弹簧振子运动过程各物理量变化规律']正确率40.0%一个弹簧振子做简谐运动。下列说法正确的是$${{(}{)}}$$
D
A.若位移为负值，则速度一定为正值
B.振子通过平衡位置时速度为零
C.振子每次通过平衡位置时速度都相同
D.振子每次通过平衡位置时速度不一定相同
8、['简谐运动的回复力和能量问题'， '弹簧振子运动过程各物理量变化规律']正确率40.0%下列有关简谐振动说法不正确的是$${{(}{)}}$$
B
A.做简谐振动的物体，受到的回复力的方向总是指向平衡位置
B.平衡位置就是加速度为零的位置
C.弹簧振子振动过程中动能和弹性势能相互转化，系统总机械能守恒
D.弹簧振子振动过程中，弹性势能增加时，弹簧的长度可能变短
9、['用牛顿运动定律分析弹簧类问题'， '受力分析'， '功能关系的应用'， '胡克定律'， '弹簧振子的回复力和能量'， '弹簧振子运动过程各物理量变化规律'， '弹簧类机械能转化问题']正确率40.0%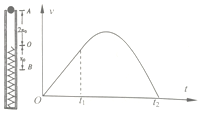
如图所示，在一直立的光滑管内放置一轻质弹簧，上端$${{O}}$$
D
A.小球运动的最大速度为$${{2}{\sqrt {{g}{{x}_{0}}}}}$$
B.小球运动到$${{O}}$$点下方$$\frac{x_{0}} {2}$$处的速度最大
C.弹簧的劲度系数为$$\frac{2 m g} {x_{0}}$$
D.弹簧的最大弹性势能为$${{3}{m}{g}{{x}_{0}}}$$
10、['弹簧振子的回复力和能量'， '弹簧振子运动过程各物理量变化规律']正确率19.999999999999996%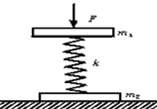
如图所示，两块质量分别为$${{m}_{1}{、}{{m}_{2}}}$$
C
A.$${{m}_{1}{g}}$$
B.$${{2}{{m}_{1}}{g}}$$
C.$$( m_{1}+m_{2} ) g$$
D.$$2 ( m_{1}+m_{2} ) g$$
1. 弹簧振子的周期公式为 $$T = 2\pi \sqrt{\frac{m}{k}}$$，与振幅无关，因此两次振动的周期之比为 $$1:1$$。振幅由初始压缩量决定，第一次为 $$x$$，第二次为 $$2x$$，故振幅之比为 $$1:2$$。正确答案为 B。
2. 振子从平衡位置 $$O$$ 向 $$B$$ 运动时，回复力 $$F = -kx$$ 逐渐增大，方向与位移相反，因此加速度 $$a = \frac{F}{m}$$ 增大，速度减小，为变减速运动。正确答案为 D。
3. 振子向平衡位置运动时，位移 $$x$$ 减小，回复力和加速度减小，速度增大，势能转化为动能。正确答案为 C。
4. 在 $$t_1$$ 到 $$t_2$$ 时间内，振子从最大位移向平衡位置运动，位移、回复力减小，速度增大，振幅不变。正确答案为 A、C。
5. 小球两次经过平衡位置 $$O$$ 时，加速度、回复力均为零，机械能守恒，但速度方向可能相反。正确答案为 D。
6. 小物块在 $$M$$ 点时回复力 $$F = -kx$$ 与位移方向相反；在 $$N$$ 点加速度 $$a = -\frac{k}{m}x$$ 相同；从 $$O$$ 向 $$M$$ 运动时做减速运动；机械能守恒。正确答案为 B。
7. 振子通过平衡位置时速度最大，方向可能为正或负，因此速度不一定相同。正确答案为 D。
8. 平衡位置是回复力为零的位置，但加速度可能不为零（如竖直弹簧振子）。弹簧长度变短时弹性势能可能增加。不正确说法为 B。
9. 小球在 $$x_0$$ 处速度为零，下落过程中动能和势能转化，最大速度 $$v = \sqrt{2gx_0}$$；速度最大位置为平衡位置 $$x = \frac{x_0}{2}$$；劲度系数 $$k = \frac{2mg}{x_0}$$；最大弹性势能 $$E_p = 2mgx_0$$。正确答案为 B、C。
10. 当 $$m_2$$ 脱离时，$$m_1$$ 受最大回复力 $$F = kx = 2m_1g$$，此时系统加速度为 $$g$$，故 $$k = \frac{2m_1g}{x}$$。对整体分析，最大拉力 $$T = (m_1 + m_2)g + kx = 2(m_1 + m_2)g$$。正确答案为 D。