.jpg)
正确率80.0%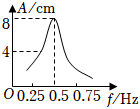
一单摆在大连的实验室中做受迫振动，其共振曲线$${{(}}$$振幅$${{A}}$$与驱动力频率$${{f}}$$的关系$${{)}}$$如图所示，则下列说法正确的是$${{(}{)}}$$
A.若把该单摆移动到漠河，要使其固有频率不变，应略微增加摆长
B.若摆长增加，共振曲线的峰将向右移动
C.此单摆的摆长约为$${{2}{m}}$$
D.若使该单摆做自由摆动$${{(}}$$摆角小于$${{5}{°}{)}}$$，则其周期大小由振幅大小决定
2、['描述简谐运动的物理量'， '单摆'， '波的干涉']正确率80.0%下列说法正确的是$${{(}{)}}$$
B
A.在同一地点，单摆做简谐振动的周期与其摆长成正比
B.弹簧振子做简谐振动时，振动系统的势能与动能之和保持不变
C.一列水波遇到障碍物发生衍射，衍射后的水波频率变化
D.已知弹簧振子初始时刻的位置及其振动周期，就可知振子在任意时刻运动速度的方向
3、['描述简谐运动的物理量'， '单摆'， '简谐运动的回复力和能量问题']正确率80.0%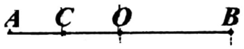
如图所示，某振子在水平方向做简谐振动，$${{O}}$$为平衡位置，$${{A}}$$、$${{B}}$$是两端最大位移处，$${{C}}$$为$${{A}{O}}$$中点，已知振动周期为$${{T}}$$，则该振子从$${{O}}$$点运动到$${{C}}$$点的最短时间为$${{(}{)}}$$
C
A.$$\frac{T} {8}$$
B.$$\frac{3 T} {8}$$
C.$$\frac{T} {1 2}$$
D.$$\frac{T} {1 6}$$
4、['简谐运动'， '单摆'， '简谐运动的回复力和能量问题']正确率80.0%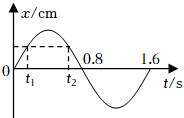
一单摆的摆动角度小于$${{5}{°}}$$，其振动图像如图所示，$${{g}}$$取$$1 0 m / s^{2}$$。下列说法正确的是$${{(}{)}}$$
A.$${{t}_{1}}$$、$${{t}_{2}}$$时刻摆球加速度方向相反
B.$${{t}{=}{{0}{.}{8}}{s}}$$时摆球的速度最大
C.单摆的振动周期为$${{0}{.}{8}{s}}$$
D.单摆的摆长约为$${{6}{4}{c}{m}}$$
5、['单摆'， '麦克斯韦电磁场理论'， '多普勒效应']正确率80.0%下列说法正确的是$${{(}{)}}$$
A.变化的磁场激发变化的电场，变化的电场激发变化的磁场
B.红光的频率低于紫光的频率，在真空中红光的传播速度大于紫光的传播速度
C.若在地球上接收到来自某遥远星球的光波的频率变低，则可判断该星球正在离我们远去
D.相同的单摆在地球纬度越高的地方，摆动的周期越大
6、['单摆']正确率80.0%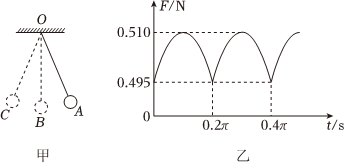
如图甲所示，$${{O}}$$点为单摆的固定悬点，将力传感器接在摆球与$${{O}}$$点之间，可测出细线对摆球的拉力大小$${{F}}$$。现将摆球拉到$${{A}}$$点，释放摆球，摆球将在竖直面内的$${{A}}$$、$${{C}}$$之间来回摆动，其中$${{B}}$$点为运动中的最低位置，图乙表示拉力大小$${{F}}$$随时间$${{t}}$$变化的曲线，图中$${{t}{=}{0}}$$为摆球从$${{A}}$$点开始运动的时刻，重力加速度$${{g}}$$取$$1 0 m / s^{2}$$。下列说法正确的是$${{(}{)}}$$
A.单摆振动的周期为$$0. 2 \pi s$$
B.单摆的摆长为$${{0}{.}{6}{m}}$$
C.摆球的质量为$$0. 0 5 k g$$
D.摆球运动过程中的最大速度为$$0. 2 m / s$$
7、['单摆']正确率80.0%关于单摆，下列说法正确的是$${{(}{)}}$$
A
A.摆球受到的回复力方向总是指向平衡位置
B.摆球受到的回复力是它所受的合外力
C.摆球经过平衡位置时，所受的合力为零
D.摆角很小时，摆球所受合力的大小跟摆球对平衡位置的位移大小成正比
8、['单摆']正确率80.0%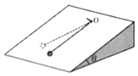
如图所示，一根不可伸长的细绳下端拴一小钢球，上端系在位于光滑斜面$${{O}}$$处的钉子上，小球处于静止状态，细绳与斜面平行。现使小球获得一平行于斜面底边的初速度，使小球偏离平衡位置，最大偏角小于$${{5}{％}}$$。已知斜面倾角为$${{θ}}$$，悬点到小球球心的距离为$${{L}}$$，重力加速度为$${{g}}$$。则小球回到最低点所需的最短时间为$${{(}{)}}$$
C
A.$$\pi\sqrt{\frac{L} {g}}$$
B.$$\pi\sqrt{\frac{L \operatorname{s i n} \theta} {g}}$$
C.$$\pi\sqrt{\frac{L} {g \operatorname{s i n} \theta}}$$
D.$$\pi\sqrt{\frac{L} {g \operatorname{c o s} \theta}}$$
9、['单摆']正确率80.0%一个单摆由甲地移到乙地后，发现走时变快了，其变快的原因及调整的方法是$${{(}{)}}$$
B
A.$$\boldsymbol{g}$$，将摆长缩短
B.$$\boldsymbol{g}$$，将摆长放长
C.$$\boldsymbol{g}$$，将摆长缩短
D.$$\boldsymbol{g}$$，将摆长放长
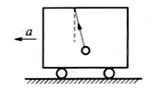
10、['单摆']正确率40.0%如图所示，在车厢中悬挂摆长为$${{l}}$$的单摆．当车厢沿水平方向以加速度$${{a}}$$运动时，则单摆相对车厢做简谐运动的周期为$${{(}{)}}$$。
D
A.$$2 \pi\sqrt{\frac{l} {g}}$$
B.$$2 \pi\sqrt{\frac{l} {a}}$$
C.$$2 \pi\sqrt{\frac{l} {g+a}}$$
D.$$2 \pi\sqrt{\frac{l} {\sqrt{g^{2}+a^{2}}}}$$
1. 解析：
根据单摆的固有频率公式 $$f = \frac{1}{2\pi}\sqrt{\frac{g}{L}}$$，漠河的$$g$$值比大连大，为保持$$f$$不变，需增加摆长$$L$$，故选项A正确。摆长增加时，固有频率减小，共振峰向左移动，选项B错误。由共振曲线可知固有频率$$f=0.25Hz$$，代入公式计算得摆长$$L \approx 4m$$，选项C错误。单摆的自由振动周期与振幅无关，选项D错误。正确答案为A。
2. 解析：
单摆周期公式为$$T=2\pi\sqrt{\frac{L}{g}}$$，周期与摆长的平方根成正比，选项A错误。弹簧振子的机械能守恒，势能与动能之和不变，选项B正确。衍射不改变波的频率，选项C错误。仅知道初始位置和周期无法确定速度方向，选项D错误。正确答案为B。
3. 解析：
简谐振动从平衡位置到中点$$C$$的相位变化为$$\frac{\pi}{6}$$，对应时间$$t=\frac{T}{12}$$，选项C正确。
4. 解析：
$$t_1$$和$$t_2$$时刻位移方向相反，加速度方向相反，选项A正确。$$t=0.8s$$时位移为零，速度最大，选项B正确。由图像可知周期$$T=1.6s$$，选项C错误。代入周期公式得摆长$$L \approx 64cm$$，选项D正确。正确答案为A、B、D。
5. 解析：
变化的电磁场相互激发形成电磁波，选项A正确。真空中所有光速相同，选项B错误。频率变低说明光源远离（红移），选项C正确。纬度越高$$g$$越大，周期越小，选项D错误。正确答案为A、C。
6. 解析：
由图像得周期$$T=0.4\pi s$$，选项A错误。代入周期公式得$$L=0.4m$$，选项B错误。在$$B$$点有$$F_{max}=mg+mv^2/L$$，在$$A$$点有$$F_{min}=mg\cos\theta$$，结合图像数据可解得质量$$m=0.05kg$$和最大速度$$v=0.2m/s$$，选项C、D正确。
7. 解析：
回复力是重力沿切线方向的分量，总指向平衡位置，选项A正确。回复力不是合外力（合外力还包括向心力），选项B错误。平衡位置处合力提供向心力不为零，选项C错误。回复力与位移成正比，但合力还包括向心力分量，选项D错误。正确答案为A。
8. 解析：
等效重力加速度为$$g_{eff}=g\cos\theta$$，周期公式为$$T=2\pi\sqrt{L/(g\cos\theta)}$$，最短时间为半个周期$$\pi\sqrt{L/(g\cos\theta)}$$，选项D正确。
9. 解析：
走时变快说明周期变小，由$$T=2\pi\sqrt{L/g}$$知可能是$$g$$增大或$$L$$减小。调整方法应增大$$L$$或减小$$g$$，但实际只能调整$$L$$。若乙地$$g$$较大，需增加$$L$$补偿；若$$g$$较小，需减小$$L$$。题目未说明$$g$$变化方向，最可能情况是乙地$$g$$较大，需增加$$L$$，选项B更合理。
10. 解析：
等效重力加速度为$$g'=\sqrt{g^2+a^2}$$，周期公式为$$T=2\pi\sqrt{l/g'}=2\pi\sqrt{l/\sqrt{g^2+a^2}}$$，选项D正确。