.jpg)
正确率60.0%潜水器在某次下潜任务中，假设某段时间内加速下潜且加速度不变，若在这段时间内$${{6}{s}}$$末的速度比$${{2}{s}}$$初的速度大$${{5}{{m}{/}{s}}{，}}$$则潜水器在该段时间内的加速度大小为（）
A
A.$${{1}{{m}{/}{s}^{2}}}$$
B.$$1. 2 5 \mathrm{m / s^{2}}$$
C.$${{2}{{m}{/}{s}^{2}}}$$
D.$${{3}{{m}{/}{s}^{2}}}$$
2、['平均速率、平均速度与瞬时速度'， '加速度的计算']正确率60.0%如图为小球在水平面上移动，每隔$${{0}{.}{0}{2}}$$秒记录下的位置。将该段运动分为$${{5}}$$段，则其中平均速度最大与平均加速度最小的运动过程分别为（）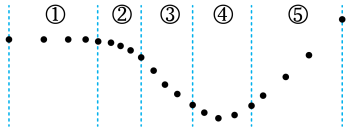
C
A.①和②
B.①和③
C.⑤和③
D.⑤和②
3、['平均速率、平均速度与瞬时速度'， '加速度的计算'， '匀变速直线运动的位移与时间的关系'， '匀变速直线运动的速度与时间的关系']正确率60.0%汽车由静止开始做匀加速直线运动，经$${{1}{s}}$$速度达到$${{3}{m}{/}{s}}$$，则$${{(}{)}}$$
B
A.在这$${{1}{s}}$$内汽车的平均速度是$${{3}{m}{/}{s}}$$
B.在这$${{1}{s}}$$内汽车的平均速度是$$1. 5 m / s$$
C.在这$${{1}{s}}$$内汽车通过的位移是$${{3}{m}}$$
D.汽车的加速度是$$1. 5 m / s^{2}$$
4、['位移差公式'， '平均速率、平均速度与瞬时速度'， '加速度的计算'， '匀变速直线运动的速度与位移的关系'， '匀变速直线运动的速度与时间的关系']正确率40.0%物体以初速度$${{v}_{0}}$$做匀减速运动，第$${{1}{s}}$$内通过的位移为$$x_{1}=6 m$$，第$${{2}{s}}$$内通过的位移为$$x_{2}=4 m$$，又经过位移$${{x}_{3}}$$物体的速度减小为$${{0}}$$，则下列说法中正确的是（）
C
A.初速度$${{v}_{0}}$$的大小为$${{8}{m}{/}{s}}$$
B.第$${{1}{s}}$$末的速度大小为$${{6}{m}{/}{s}}$$
C.位移$${{x}_{3}}$$的大小为$$2. 2 5 m$$
D.位移$${{x}_{3}}$$内的平均速度大小为$${{2}{m}{/}{s}}$$
5、['加速度的计算']正确率60.0%$${{2}{0}{1}{4}}$$年$${{9}}$$月$${{2}{6}}$$日，在仁川亚运会男子蹦床比赛中，中国选手董栋以$$6 2. 4 8 0$$分的成绩夺冠，他的队友涂潇以$$6 0. 4 3 5$$分的成绩获得银牌，为国争得了荣誉．如果董栋在比赛中，从高处自由落下，以$$v_{1}=8 m / s$$的竖直速度着网，与网作用后，沿着竖直方向以$$v_{2}=1 0 m / s$$的速度弹回．已知运动员与网接触的时间为$$\triangle t=1. 2 s.$$那么运动员在与网接触的这段时间内平均加速度的大小和方向分别为（）
B
A.$$1 5 m / s^{2}$$，竖直向下
B.$$1 5 m / s^{2}$$，竖直向上
C.$$1. 6 7 m / s^{2}$$，竖直向上
D.$$1. 6 7 m / s^{2}$$，竖直向下
6、['平抛运动基本规律及推论的应用'， '加速度的计算'， '其他抛体运动'， '从运动情况确定受力'， '位移与路程的计算']正确率40.0%从同一高度以相同的速率分别抛出质量相等的三个小球，一个竖直上抛，一个竖直下抛，另一个水平抛出，最终落到同一水平面上．则它们在空中运动的过程中（）
B
A.运动的时间相等
B.加速度相同
C.运动的路程相同
D.运动的位移相同
7、['加速度的计算'， '匀变速直线运动的位移与时间的关系']正确率60.0%物体在光滑斜面顶端由静止开始匀加速下滑，最初$${{4}{s}}$$内经过的位移为$${{S}_{1}}$$，最后$${{4}{s}}$$内经过的位移为$${{S}_{2}}$$，且$$S_{2}-S_{1}=8 m， ~ S_{1} \colon~ S_{2}=1 \colon2$$.则物体运动的加速度及斜面长度分别为$${{(}{)}}$$
A
A.$$1 m / s^{2}， 1 8 m$$
B.$$0. 5 m / s^{2}， ~ 9$$$${{m}}$$
C.$$0. 1 m / s^{2}， ~ 8$$$${{m}}$$
D.$$0. 1 m / s^{2}， ~ 1. 8$$$${{m}}$$
8、['用牛顿运动定律分析斜面体模型'， '加速度的计算']正确率40.0%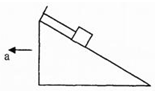
如图所示，质量为$${{m}}$$
D
A.$${{g}{{s}{i}{n}}{θ}}$$
B.$${{g}{{c}{o}{s}}{θ}}$$
C.$${{g}{{t}{a}{n}}{θ}}$$
D.$${{g}{{c}{o}{t}}{θ}}$$
9、['匀变速直线运动平均速度和中间时刻速度公式'， '加速度的计算'， '匀变速直线运动的位移与时间的关系']正确率40.0%甲乙两辆汽车在平直的公路上沿同一方向做匀变速直线运动，$${{t}{=}{0}}$$时刻同时经过公路旁的同一路标，下表是每隔$${{1}{s}}$$记录的两车的速率．关于两车的运动，下列说法正确的是$${{(}{)}}$$
| 时间 $${{t}{/}{s}}$$ | $${{0}}$$ | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ | $${{4}}$$ |
| 甲车的速率 $$v_{1} / ( m \cdot s^{-1} )$$ | $${{1}{8}{.}{0}}$$ | $${{1}{6}{.}{0}}$$ | $${{1}{4}{.}{0}}$$ | $${{1}{2}{.}{0}}$$ | $${{1}{0}{.}{0}}$$ |
| 乙车的速率 $$v_{2} / ( m \cdot s^{-1} )$$ | $${{3}{.}{0}}$$ | $${{4}{.}{0}}$$ | $${{5}{.}{0}}$$ | $${{6}{.}{0}}$$ | $${{7}{.}{0}}$$ |
D
A.乙车的速度变化较快
B.在$${{0}{∼}{4}{s}}$$内，乙车的平均速度较大
C.在$${{0}{∼}{4}{s}}$$内，甲车相对乙车行驶了$${{5}{6}{m}}$$
D.在乙车追上甲车之前，$${{t}{=}{5}{s}}$$时两车相距最远
10、['加速度的计算'， '利用平衡推论求力'， '牛顿第二定律的简单应用']正确率40.0%一个质量为$${{m}}$$的物体，在几个共点力作用下做匀速直线运动，在$${{t}{=}{0}}$$时刻，将其中的一个力大小由$${{F}}$$变为$${{3}{F}}$$，方向不变，其它力保持不变，则从$${{t}{=}{0}}$$时刻到$${{t}{=}{{t}_{0}}}$$时刻的过程中，物体速度变化量的大小为（）
A
A.$$\frac{2 F t_{0}} {m}$$
B.$$\frac{4 F t_{0}} {m}$$
C.$$\frac{6 F t_{0}} {m}$$
D.$$\frac{8 F t_{0}} {m}$$
1. 潜水器在6秒末和2秒初的时间差为4秒，速度差为5 m/s，由加速度定义 $$a = \frac{\Delta v}{\Delta t} = \frac{5}{4} = 1.25 \, \text{m/s}^2$$，故选 B。
2. 平均速度最大的过程是位移最大的⑤，平均加速度最小的过程是速度变化最慢的③，故选 C。
3. 汽车匀加速运动，平均速度 $$v_{\text{avg}} = \frac{v_0 + v}{2} = \frac{0 + 3}{2} = 1.5 \, \text{m/s}$$，位移 $$x = v_{\text{avg}} \cdot t = 1.5 \times 1 = 1.5 \, \text{m}$$，加速度 $$a = \frac{v - v_0}{t} = 3 \, \text{m/s}^2$$，故选 B。
4. 由匀减速运动规律，$$x_1 - x_2 = aT^2$$ 得 $$a = -2 \, \text{m/s}^2$$，初速度 $$v_0 = \frac{x_1 + \frac{1}{2}aT^2}{T} = 7 \, \text{m/s}$$，第1秒末速度 $$v_1 = v_0 + aT = 5 \, \text{m/s}$$，位移 $$x_3 = \frac{v_2^2}{2a} = 2.25 \, \text{m}$$，平均速度 $$v_{\text{avg}} = \frac{v_2}{2} = 2 \, \text{m/s}$$，故选 C 和 D。
5. 平均加速度 $$a = \frac{\Delta v}{\Delta t} = \frac{10 - (-8)}{1.2} = 15 \, \text{m/s}^2$$，方向与弹回方向相同（竖直向上），故选 B。
6. 三个小球加速度均为重力加速度 $$g$$，方向竖直向下，故选 B。
7. 由 $$S_2 - S_1 = 8 \, \text{m}$$ 和 $$S_1 : S_2 = 1 : 2$$ 得 $$S_1 = 8 \, \text{m}$$，$$S_2 = 16 \, \text{m}$$。由 $$S_1 = \frac{1}{2} a t_1^2$$ 得 $$a = 1 \, \text{m/s}^2$$，总时间 $$t = 6 \, \text{s}$$，斜面长度 $$L = \frac{1}{2} a t^2 = 18 \, \text{m}$$，故选 A。
8. 题目不完整，无法解析。
9. 甲车加速度 $$a_1 = -2 \, \text{m/s}^2$$，乙车加速度 $$a_2 = 1 \, \text{m/s}^2$$，乙车速度变化较慢。0~4秒内，甲车平均速度 $$v_{\text{avg1}} = \frac{18 + 10}{2} = 14 \, \text{m/s}$$，乙车平均速度 $$v_{\text{avg2}} = \frac{3 + 7}{2} = 5 \, \text{m/s}$$，甲车相对位移 $$\Delta x = (14 - 5) \times 4 = 36 \, \text{m}$$。两车速度相等时（$$t = 5 \, \text{s}$$）相距最远，故选 D。
10. 合力变化量 $$\Delta F = 2F$$，由动量定理 $$\Delta p = \Delta F \cdot t_0 = 2F t_0$$，速度变化量 $$\Delta v = \frac{\Delta p}{m} = \frac{2F t_0}{m}$$，故选 A。